
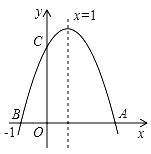
① ;②
;③抛物线与
轴的另一个交点是
;④方程
有两个不相等的实数根;⑤
;⑥不等式
的解集为
.其中结论正确的是( )


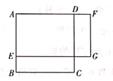


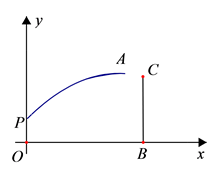

如图所示,图中点的横坐标x表示科技馆从8:30开门后经过的时间(分钟),纵坐标y表示到达科技馆的总人数.图中曲线对应的函数解析式为y= ,10:00之后来的游客较少可忽略不计.
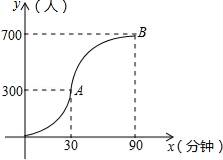
如图,在平面直角坐标系中,抛物线y=ax2+x+c(a≠0)与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,点A的坐标为(4,0),抛物线的对称轴是直线x=
.



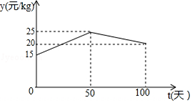
①分别求出当 和
时,
与
的函数关系式;
②设将这批淡水鱼放养 天后一次性出售所得利润为
元,求当
为何值时,
最大?并求出最大值.(利润
销售总额-总成本)
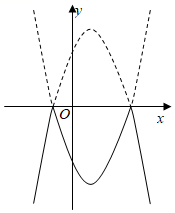
①当图象G的最高点的纵坐标与点P的纵坐标之差为1时,求m的值.
②将点P向左平移4个单位长度得到点Q,连结PQ.以PQ为边向上方作矩形PQMN,使PN=2,当图象G在矩形PQMN内的部分所对应的函数值y随x的增大而增大时,直接写出m的取值范围.