浙教版备考2022年中考数学一轮复习专题19 图形初步

更新时间：2022-01-13 浏览次数：131 类型：一轮复习

一、单选题

1. (2021八上·温州期中) “三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图所示的“三等分角仪”能三等分任意一角.这个三等分角仪由两根有槽的棒OA、OB组成，两根棒在O点相连并可绕O转动，C点固定，OC＝CD＝DE，点D、E可在槽中滑动，若∠ODE＝99°，则∠CDE的度数是（）

A . 68° B . 69° C . 72° D . 75°

答案解析收藏纠错 + 选题
2. (2021八上·台州期中) 已知 $\text{[math]}$ ，用尺规作图的方法在 BC上取一点P，使 $\text{[math]}$ ，下列选项正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2021八上·金华期中) 下列命题中，①在同一平面内，若 a⊥b ， $\text{[math]}$ ，则 $\text{[math]}$ ；②相等的角是对顶角；③能被2整除的数也能被4整除；④两点之间线段最短.真命题有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
4. 如图所示是一个三级台阶，它的每一级的长、宽、高分别2F为20 dm，3 dm，2 dm，A和B是这个台阶。上两个相对的端点，点A处有一只蚂蚁，想到点B处去吃可口的食物，则蚂蚁沿着台阶面爬行到点B的最短路程为（）

A . 20dm B . 25 dm C . 30 dm D . 35 dm

答案解析收藏纠错 + 选题
5. 如图，已知∠1=∠2，则∠3的角平分线与∠4的角平分线（）

A . 互相平行 B . 相交 C . 平行或相交 D . 重合

答案解析收藏纠错 + 选题
6. 将一个直角三角形绕它的最长边(斜边)旋转一周，得到的几何体是（）．

A . B . C . D .

答案解析收藏纠错 + 选题
7. 如图 $\text{[math]}$ ，以 $\text{[math]}$ 为边作 $\text{[math]}$ ，使 $\text{[math]}$ ，那么下列说法正确的是（）

A . $\text{[math]}$ B . ∠AOC=∠AOB C . $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021九上·台州期中) 如图，在Rt△ABC中，∠ABC=90°，AB=BC，点P在△ABC内一点，连接PA，PB，PC，若∠BAP=∠CBP，且AP = 6，则PC的最小值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021九上·义乌期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，AB=AC=5，点 $\text{[math]}$ 在 $\text{[math]}$ 上，且 $\text{[math]}$ ，点E是AB上的动点，连结 $\text{[math]}$ ，点 $\text{[math]}$ ，G分别是BC，DE的中点，连接 $\text{[math]}$ ， $\text{[math]}$ ，当AG=FG时，线段 $\text{[math]}$ 长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题
10. 如图，一张矩形纸片沿AB对折，以AB中点O为顶点将平角五等分，并沿五等分的折线折叠，再沿CD剪开，使展开后为正五角星（正五边形对角线所构成的图形），则∠OCD等于（）

A . 108° B . 114° C . 126° D . 129°

答案解析收藏纠错 + 选题

二、填空题

11.
1. （1）十边形的一个顶点的对角线把十边形分成个三角形．
2. （2）正多边形是指，的多边形．
答案解析收藏纠错 + 选题
12. (2021八上·温州期中) 如图，在直角三角形ABC中，∠ACB＝90°，AB＝7，点D是AB的中点，点P是斜边AB上的一个动点，FG是线段CP的垂直平分线，Q是FG上的一个动点，则PQ+QD的最小值为.

答案解析收藏纠错 + 选题
13. (2023八上·苍南月考) 如图，若∠α=38°，根据尺规作图的痕迹，则∠AOB的度数为．

答案解析收藏纠错 + 选题
14. (2021七上·莘县期中) 从棱长为2的正方体毛坯的一角，挖去一个棱长为1的小正方体，得到一个如图所示的零件，则这个零件的表面积为．

答案解析收藏纠错 + 选题
15. (2018八上·河南期中) 在底面直径为2cm，高为3cm的圆柱体侧面上，用一条无弹性的丝带从A至C按如图所示的圈数缠绕，则丝带的最短长度为cm．（结果保留π）

答案解析收藏纠错 + 选题
16. 一块方形蛋糕，一刀切成相等的两块，两刀最多切成4块，试问：五刀最多可切成块相等体积的蛋糕，十刀最多可切成块（要求：竖切，不移动蛋糕）．

答案解析收藏纠错 + 选题

三、综合题

17. (2024八下·印江月考) 如图，在△ABC中，∠B=∠C，过BC的中点D作DE⊥AB，DF⊥AC，垂足分别为点E，F．
1. （1）求证：DE=DF；
2. （2）若∠BDE =40°，求∠BAC的度数．
答案解析收藏纠错 + 选题
18. 如图，在△ABC中，∠ACB=90°，以点B为圆心，BC长为半径画弧，交线段AB于点D，以点A为圆心，AD长为半径画弧，交线段AC于点E，连接CD．
1. （1）若CA=28° ，求∠ACD的度数；
2. （2）若BC=3，AC=4，求AD的长．
答案解析收藏纠错 + 选题
19. 在△ABC中，DE垂直平分AB，分别交AB、BC于点D、E，MN垂直平分AC，分别交AC、BC于点M、N．
1. （1）如图①，若∠BAC=110°，求∠EAN的度数；
2. （2）如图②，若∠BAC=80°，求∠EAN的度数；
3. （3）若∠BAC=α(α≠90°)，直接写出∠EAN的大小(用含α的代数式表示)．
答案解析收藏纠错 + 选题
20. 用一块纸板做一个有底无盖的正方体粉笔盒，已知粉笔盒的容积为216cm³ ．
1. （1）这个粉笔盒的棱长为多少？
2. （2）这块纸板的面积至少要多大？
答案解析收藏纠错 + 选题
21. 如图所示是一个长方体的展开图，每个面上都标注了字母，请根据要求回答问题：
1. （1）如果面A在多面体的上面，那么哪一面会在下面?
2. （2）如果面F在多面体的后面，从左面看是面B，那么哪一面会在上面?
3. （3）从右面看是面A，从上面看是面E，那么哪一面会在前面?
答案解析收藏纠错 + 选题
22. 如图，圆锥底面的半径为10cm，高为10 $\text{[math]}$ cm．
1. （1）求圆锥的全面积；
2. （2）若一只蚂蚁从底面上一点A出发绕圆锥一周回到SA上一点M处，且SM=3AM，求它所走的最短距离．
答案解析收藏纠错 + 选题
23. 如图，直线 $\text{[math]}$ 相交于点 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ .
1. （1）若 $\text{[math]}$ ，则 $\text{[math]}$ =；
2. （2）若 $\text{[math]}$ =2 cm， $\text{[math]}$ =1.5 cm， $\text{[math]}$ =2.5 cm，则点 $\text{[math]}$ 到 $\text{[math]}$ 的距离是cm.
答案解析收藏纠错 + 选题
24. 已知∠A=72°15′48″，∠B=35°30′43″．
1. （1）求∠B的余角与∠A的补角的和；
2. （2）求∠A+2∠B的度数．
答案解析收藏纠错 + 选题
25. 一副三角板ABC、DBE如图1放置，（∠D=30°、∠BAC=45°）
1. （1）求∠DBA的度数；
2. （2）若三角板DBE绕B点逆时针旋转，（如图2）在旋转过程中BM、BN分别平分∠DBA、∠EBC，则∠MBN如何变化；
3. （3）若三角板DBE绕B点逆时针旋转到如图3时，其它条件不变，则（2）的结论是否变化？
答案解析收藏纠错 + 选题
26. (2021七上·金华期中) （阅读理解）：A，B，C为数轴上三点，若点C到A的距离CA是点C到B的距离CB的2倍，就称点C是（A，B）的好点．例如，如图1，点A表示的数为－1，点B表示的数为2．表示1的点C到点A的距离CA是2，到点B的距离CB是1，那么点C是（A，B）的好点；又如，表示0的点D到点A的距离DA是1，到点B的距离DB是2，那么点D就不是（A，B)的好点，但点D是（B，A)的好点．
（知识运用）：
1. （1）如图1，表示数和的点是（A，B）的好点；
2. （2）如图2，M、N为数轴上两点，点M所表示的数为－2，点N所表示的数为4．
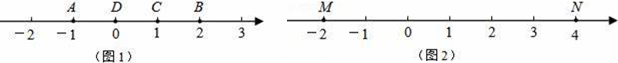
  ①表示数的点是（M，N)的好点；
  
  ②表示数的点是（N，M)的好点；
3. （3）如图3，A、B为数轴上两点，点A所表示的数为－20，点B所表示的数为40．现有一只电子蚂蚁P从点B出发，以2个单位每秒的速度向左运动．当t为何值时，P、A和B中恰有一个点为其余两点的好点?
答案解析收藏纠错 + 选题
27. (2021七上·镇海期中) 如图
1. （1）【新知理解】
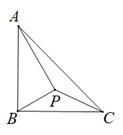
  点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，若 $\text{[math]}$ 或 $\text{[math]}$ ，则称点 $\text{[math]}$ 是线段 $\text{[math]}$ 的 “优点”，线段 $\text{[math]}$ 称作互为"优点"伴侣线段。例如，图1，线段 $\text{[math]}$ 的长度为6 ，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ 的长度为2 ，则点 $\text{[math]}$ 是线段 $\text{[math]}$ 的其中一个 “优点”。
  
  ①若点 $\text{[math]}$ 为图1中线段 $\text{[math]}$ 的 “优点” $\text{[math]}$ ，则 $\text{[math]}$ 。
  
  ②若点 $\text{[math]}$ 也是图1中线段 $\text{[math]}$ 的 “优点” (不同于点 $\text{[math]}$ )，则ACBD.(填 “ $\text{[math]}$ 或 “#”)
2. （2）【解决问题】
  如图 2，数轴上有一点 $\text{[math]}$ 表示的数为1，向右平移3个单位到达点 $\text{[math]}$ ；
  
  ③若不同的两点 $\text{[math]}$ 都在线段OF上，且 $\text{[math]}$ 均为线段OF的“优点”，求线段 MN 的长；
  
  ④如图2，若点 $\text{[math]}$ 在射线 $\text{[math]}$ 上，且线段 $\text{[math]}$ 与以 $\text{[math]}$ 中某两个点为端点的线段互为 “优点” 伴侣线段，求点 $\text{[math]}$ 表示的数 (写出所有可能)。
答案解析收藏纠错 + 选题
28. 已知：在四边形ABCD中，对角线AC，BD相交于点E，且AC⊥BD，作BF⊥CD，垂足为点F，BF与AC交于点G，∠BGE=∠ADE．
1. （1）如图①所示，试说明：AD=CD．．
2. （2）如图②所示，BH是△ABE的中线，若AE=2DE，DE=EG，在不添加任何辅助线的情况下，请直接写出图②中四个三角形，使写出的每个三角形的面积都等于△ADE面积的2倍．
答案解析收藏纠错 + 选题
29. 已知线段AB=6．
1. （1）取线段AB的三等分点，这些点连同线段AB的两个端点可以组成多少条线段？求这些线段长度的和；
2. （2）再在线段AB上取两种点：第一种是线段AB的四等分点；第二种是线段AB的六等分点，这些点连同（1）中的三等分点和线段AB的两个端点可以组成多少条线段？求这些线段长度的和。
答案解析收藏纠错 + 选题