题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

山东省济南市章丘区2021-2022学年九年级上学期期末数学...

更新时间：2024-07-13 浏览次数：108 类型：期末考试

一、单选题

1. (2021九上·章丘期末) 如图，一个水晶球摆件，它是由一个长方体和一个球体组成的几何体，则其主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2021九上·章丘期末) 已知 $\text{[math]}$ ，则下列比例式成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021九上·章丘期末) 反比例函数的图象经过点（﹣2，3），则此函数的图象也经过点（）

A . （2，﹣3） B . （﹣3，﹣3） C . （2，3） D . （﹣4，6）

答案解析收藏纠错 + 选题
4. (2021九上·章丘期末) 如图，△ABC中，点D、E分别为边AB和AC中点，且S_△ADE=3，则S_△ABC等于（）

A . 4 B . 8 C . 9 D . 12

答案解析收藏纠错 + 选题
5. (2024九上·泾阳期末) 在一个不透明的袋子中有除颜色外均相同的6个白球和若干黑球，通过多次摸球试验后，发现摸到白球的频率约为30%，估计袋中黑球有（）个．

A . 8 B . 9 C . 14 D . 15

答案解析收藏纠错 + 选题
6. (2023九上·历城期末) 已知点A（﹣1，y₁）、B（﹣3，y₂）、C（ $\text{[math]}$ ，y₃）在反比例函数y＝﹣ $\text{[math]}$ 的图象上，则y₁、y₂、y₃的大小关系正确的是（）

A . y₁＞y₂＞y₃ B . y₂＞y₁＞y₃ C . y₂＞y₃＞y₁ D . y₃＞y₁＞y₂

答案解析收藏纠错 + 选题
7. (2024九上·龙江月考) 关于x的方程x²＋mx＋6＝0的一个根为－2，则另一个根是（）

A . －3 B . －6 C . 3 D . 6

答案解析收藏纠错 + 选题
8. 下列命题正确的是（）

A . 对角线相等的四边形是平行四边形 B . 对角线相等的四边形是矩形 C . 对角线互相垂直的平行四边形是菱形 D . 对角线互相垂直且相等的四边形是正方形

答案解析收藏纠错 + 选题
9. (2021九上·章丘期末) 已知关于x的方程 $\text{[math]}$ ，则下列关于该方程根的判断，正确的是（）

A . 没有实数根 B . 有两个相等的实数根 C . 有两个不相等的实数根 D . 不能确定

答案解析收藏纠错 + 选题
10. (2021九上·章丘期末) 在同一平面直角坐标系中，函数y＝kx+k与y＝ $\text{[math]}$ （k≠0）的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
11. (2022·信都模拟) 如图，矩形ABCD中，AB=8cm，AD=6cm，EF是对角线BD的垂直平分线，则EF的长为（）cm．

A . $\text{[math]}$ B . 5 C . $\text{[math]}$ D . 8

答案解析收藏纠错 + 选题
12. (2021九上·章丘期末) 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ ， $\text{[math]}$ 边上的两个动点，且 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 中点，则 $\text{[math]}$ 的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2021九上·章丘期末) 一个布袋里装有2个只有颜色不同的球，其中1个红球，1个白球，从布袋里摸出1个球，记下颜色后放回，搅匀，再摸出1个球，则两次摸到的球恰好颜色不同的概率是．

答案解析收藏纠错 + 选题
14. (2021九上·章丘期末) 如图，是小莹设计用手电来测量某古城墙高度的示意图．在点P处放一水平的平面镜，光线从点A出发经平面镜反射后，刚好射到古城墙CD的顶端C处．已知AB⊥BD， $\text{[math]}$ ．且测得 $\text{[math]}$ 米， $\text{[math]}$ 米，PD=12米，那么该古墙的高度是米．

答案解析收藏纠错 + 选题
15. (2022八下·临清期中) 如图，在菱形ABCD中，已知AB＝5，AC＝6，那么菱形ABCD的面积为．

答案解析收藏纠错 + 选题
16. (2023九上·历城期末) 某商品经过两次连续提价，每件售价由原来的100元上涨到了121元．设平均每次涨价的百分率为x，则x是．

答案解析收藏纠错 + 选题
17. (2021九上·章丘期末) 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，已知AD=5，BD=4，那么BC=．

答案解析收藏纠错 + 选题
18. (2021九上·章丘期末) 如图，点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，且 $\text{[math]}$ ，直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的坐标是．

答案解析收藏纠错 + 选题

三、解答题

19. (2024九上·贵州期末) 解方程： $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2021九上·章丘期末) 已知：如图， $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 的边 $\text{[math]}$ 、 $\text{[math]}$ 上的点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．求 $\text{[math]}$ 的长度．

答案解析收藏纠错 + 选题
21. (2021九上·章丘期末) 如图，四边形ACMF、BCNE 是两个正方形．求证：AN＝BM ．

答案解析收藏纠错 + 选题
22. (2021九上·章丘期末) 如图，学校打算用16m的篱笆围成一个长方形的生物园饲养小兔，生物园的一面靠墙（如图，墙长9m），面积是30m² ．求生物园的长和宽．

答案解析收藏纠错 + 选题
23. (2021九上·章丘期末) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ，对角线 $\text{[math]}$ 的垂直平分线与边 $\text{[math]}$ 、 $\text{[math]}$ 分别相交于点 $\text{[math]}$ 、 $\text{[math]}$ .
1. （1）求证：四边形 $\text{[math]}$ 是菱形；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求菱形 $\text{[math]}$ 的周长.
答案解析收藏纠错 + 选题
24. (2023·沁阳模拟) 某学校为了解全校学生对电视节目（新闻、体育、动画、娱乐、戏曲）的喜爱情况，从全校学生中随机抽取部分学生进行问卷调查，并把调查结果绘制成两幅不完整的统计图.

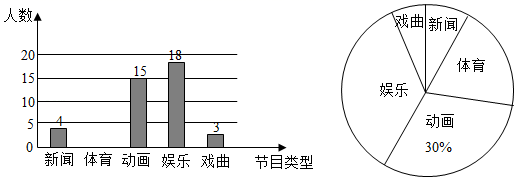
请根据以上信息，解答下列问题
1. （1）这次被调查的学生共有多少名？
2. （2）请将条形统计图补充完整；
3. （3）若该校有3000名学生，估计全校学生中喜欢体育节目的约有多少名？
4. （4）该校宣传部需要宣传干事，现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名，用树状图或列表法求恰好选中甲、乙两位同学的概率.
答案解析收藏纠错 + 选题
25. (2021九上·章丘期末) 如图
1. （1）感知：数学课上，老师给出了一个模型：
  如图1， $\text{[math]}$ ，由 $\text{[math]}$ ， $\text{[math]}$ ，可得 $\text{[math]}$ ；又因为 $\text{[math]}$ ，可得 $\text{[math]}$ ，进而得到 $\text{[math]}$ ．我们把这个模型称为“一线三等角”模型．
2. （2）应用：实战组受此模型的启发，将三等角变为非直角，如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点P是BC边上的一个动点（不与B、C重合），点D是AC边上的一个动点，且 $\text{[math]}$ ．
  ①求证： $\text{[math]}$ ；
  ②当点P为BC中点时，求CD的长；
3. （3）拓展：在（2）的条件下如图2，当 $\text{[math]}$ 为等腰三角形时，请直接写出BP的长．
答案解析收藏纠错 + 选题
26. (2021九上·章丘期末) 如图，已知一次函数图象y=x+b与y轴交于点C（0，1），与反比例函数图象y= $\text{[math]}$ 交于点A（a，2）和点B两点．
1. （1）求一次函数和反比例函数的解析式；
2. （2）求点B的坐标和△AOB的面积；
3. （3）若点M为y轴上的一个动点，N为平面内一个动点，当以A、B、M、N为顶点的四边形是矩形时，请求出M点坐标．
答案解析收藏纠错 + 选题
27. (2021九上·章丘期末) 如图1，在Rt△ABC中，∠BAC=90°，∠ACB=60°，AC=2，点A₁ ， B₁为边AC，BC的中点，连接A₁B₁ ，将△A₁B₁C绕点C逆时针旋转α（0°≤α≤360°）．
1. （1）如图1，当α=0°时， $\text{[math]}$ ，BB₁ ， AA₁所在直线相交所成的较小夹角的度数为；
2. （2）将△A₁B₁C绕点C逆时针旋转至图2所示位置时，（1）中结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；
3. （3）当△A₁B₁C绕点C逆时针旋转过程中，
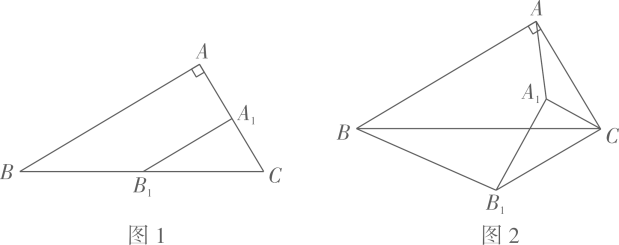
  ①请直接写出△ABA₁面积的最大值；
  ②当A₁ ， B₁ ， B三点共线时，请直接写出线段BB₁的长．
答案解析收藏纠错 + 选题

试卷信息