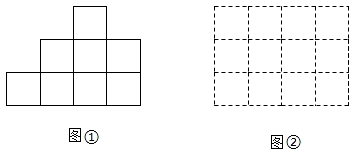
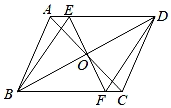
①BE+DF=EF;②tan∠AMD=;③BM2+DN2=MN2;④若EF=1.5,△AEF的面积是3,则正方形ABCD的面积是4.



七年级抽取的学生在C组的课外劳动时间为:40,40,50,55
八年级抽取的20名学生的课外劳动时间为:10,15,20,25,30,35,40,40,45,50,50,50,55,60,60,75,75,80,90,95
七年级抽取的学生的课外劳动时间的扇形统计图

七,八年级抽取的学生的课外劳动时间的统计量
| 年级 | 平均数 | 众数 | 中位数 | 方差 |
| 七年级 | 50 | 35 | | 580 |
| 八年级 | 50 | | 50 | 560 |
根据以上信息,解答下列问题:

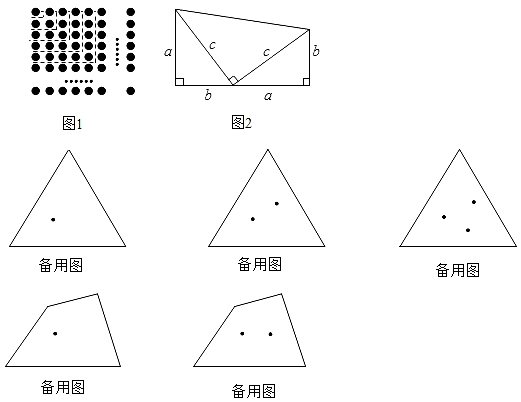
数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也称做富比尼原理,是一种重要的数学思想.
例如:
图1,将n行n列的棋子排成一个正方形,我们用两种不同的方法计算棋子的个数:
算法Ⅰ:
类比正方形面积的计算,图形可以看作n行棋子,每行都有n枚,因此棋子的总数是:
n×n=n2
算法Ⅱ:
沿虚线将图案分割,可以发现:
第一层虚线内有1枚棋子,
第二层虚线内有3枚棋子,
第三层虚线内有5枚棋子…
第n层虚线内有(2n﹣1)枚棋子,
则棋子总数为1+3+5+7+…+2n﹣1
由此可得:1+3+5+7+…+2n﹣1=n2
如图2,两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成一个梯形.请用两种不同的方法计算梯形的面积,并写出你发现的结论.
算法Ⅰ:
算法Ⅱ:
你发现的结论是.
经过整理,这个结论恰好可以证明我们学过的重要定理.
富比尼原理给我们重要的启发:
从同一个问题的不同角度展开探究,往往会有惊喜地发现.
问题:
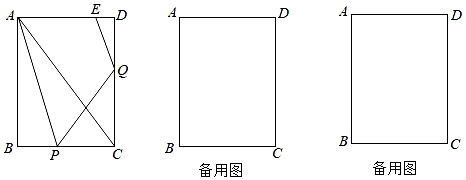
n边形有n个顶点,在它的内部再画m个点,以这(m+n)个点为顶点,把n边形剪成若干个三角形,设最多可以剪得y个这样的三角形.可以用含m、n的代数式表示y吗?
问题探究:
为了解决这个问题,我们先从简单的情况入手:
(一)研究最简单的多边形﹣﹣三角形.
三角形有3个顶点,在它的内部再画m个点,把三角形剪成若干个三角形,设最多可以剪得y个这样的三角形,那么可以用含有m的代数式来表示y吗?
方法Ⅰ:关注要素﹣﹣三角形内部每增加一个点,与最多可以剪得多少个三角形之间的关系.
从n=3,m=1开始研究:
当n=3,m=1时,最多可以把原三角形剪成3个三角形;
当n=3,m=2时,最多可以把原三角形剪成(3+2)个三角形;
当n=3,m=3时,最多可以把原三角形剪成(5+2)个三角形;
…
进行从特殊到一般的归纳:
对于一般的情形,在三角形内画m个点,第一个点将三角形分成了3个三角形,三角形内部每增加一个点,可增加个三角形.
故n=3时,用含有m的代数式表示y=;
方法Ⅱ:关注要素﹣﹣顶点数对组成三角形的作用.
三角形的三个顶点和它内部的1个点,共4个点,以这4个点为顶点,最多可以组成3个互不重叠的小三角形.
三角形的三个顶点和它内部的2个点,共5个点,以这5个点为顶点,最多可以组成5个互不重叠的小三角形.
三角形的三个顶点和它内部的3个点,共6个点,以这6个点为顶点,最多可以组成7个互不重叠的小三角形.
…
进行从特殊到一般的归纳:
三角形的三个顶点和它内部的m个点,共(m+3)个点,以这(m+3)个点为顶点,最多可以组成个互不重叠的小三角形.
以三角形的三个顶点和它内部的m个点,可把三角形最多剪成个互不重叠的小三角形.
(二)在四边形中研究类似的问题.
四边形有4个顶点,在它的内部再画m个点,把四边形剪成若干个三角形,设最多可以剪得y个三角形,那么可以用含有m的代数式来表示y吗?
方法Ⅰ:
对于一般的情形,在四边形内画m个点,第一个点将四边形分成了4个三角形;四边形内部每增加一个点,可增加个三角形.
故n=4时,用含有m的代数式来表示y:y=.
方法Ⅱ:
四边形的四个顶点和它内部的m个点,共(m+4)个点,以这(m+4)个点为顶点,最多可以组成个互不重叠的小三角形.
对于一般的情形,在n边形内画m个点,通过多角度探究、归纳猜想和算两遍方法的验证,可得y=(用含m、n的代数式表示).