题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

2022年浙教版数学七下期末复习阶梯训练：分式（优生集训）

更新时间：2022-05-12 浏览次数：86 类型：复习试卷

一、综合题

1.
1. （1）【探索】
  ①如果 $\text{[math]}$ ，则 $\text{[math]}$ .
  
  ②如果 $\text{[math]}$ ，则 $\text{[math]}$ .
2. （2）【总结】如果 $\text{[math]}$ (其中a，b，c为常数)，则m=.
3. （3）【应用】利用上述结论解决：若代数式 $\text{[math]}$ 的值为整数，求满足条件的整数 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
2. (2020七下·鄞州期末) 用如图所示的甲、乙、丙三块木板做一个长、宽、高分别为a厘米，b厘米和10厘米的长方体木箱，其中甲块木板锯成两块刚好能做箱底和一个长侧面，乙块木板刚好能做一个长侧面和一个短侧面，丙块木板刚好能做一个箱盖和剩下的一个短侧面（厚度忽略不计，a＞b）
1. （1）用含a，b的代数式分别表示这三块木板的面积.
2. （2）若甲块木板的面积比丙块木板的面积大200平方厘米，木箱的体积为150000立方厘米，求乙块木板的面积.
3. （3）如果购买一块长为100厘米，宽为（a+b）厘米的长方形木板做这个木箱，木板的利用率为90%，试求分式 $\text{[math]}$ + $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
3. (2019七下·吴兴期末) 湖州奥体中心是一座多功能的体育场，目前体育场内有一块长80m，宽60m的长方形空地，体育局希望将其改建成花园小广场，设计方案如图，阴影区域是面积为192平方米的绿化区（四块相同的直角三角形），空白区域为活动区，且四周出口宽度一样.
1. （1）体育局先对四个绿化区域进行绿化，在完成工作量的 $\text{[math]}$ 后，施工方进行了技术改进，每天的绿化面积是原计划的两倍，结果提前四天完成四个绿化区域的改造，问原计划每天绿化多少平方米？
2. （2）老师提出了一个问题：你能不能求出活动区的出口宽度是多少呢？
  
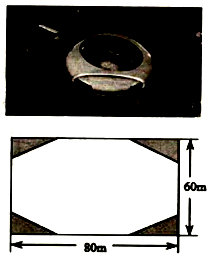
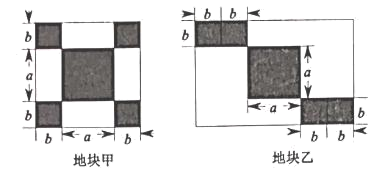
  请你根据小丽的方法求出活动区的出口宽度，并把过程写下来.
答案解析收藏纠错 + 选题
4. (2019七下·安徽期末) 北京奥运会开幕前，某体育用品商场预测某品牌运动服能够畅销，就用32000元购进了一批这种运动服，上市后很快脱销，商场又用68 000元购进第二批这种运动服，所购数量是第一批购进数量的2倍，但每套进价多了10元．
1. （1）该商场两次共购进这种运动服多少套？
2. （2）如果这两批运动服每套的售价相同，且全部售完后总利润率不低于20%，那么每套售价至少是多少元？（利润率= $\text{[math]}$ ×100%）
答案解析收藏纠错 + 选题
5. 阅读材料：
关于x的方程： $\text{[math]}$ 的解是 $\text{[math]}$ ， $\text{[math]}$ ；

$\text{[math]}$ （即 $\text{[math]}$ ）的解是 $\text{[math]}$ $\text{[math]}$ ；

$\text{[math]}$ 的解是 $\text{[math]}$ ， $\text{[math]}$ ；

$\text{[math]}$ 的解是 $\text{[math]}$ ， $\text{[math]}$ ；……
1. （1）请观察上述方程与解的特征，比较关于x的方程 $\text{[math]}$ 与它们的关系，猜想它的解是什么？并利用“方程的解”的概念进行验证。
2. （2）由上述的观察、比较、猜想、验证，可以得出结论：
  如果方程的左边是未知数与其倒数的倍数的和，方程的右边的形式与左边完全相同，只是把其中的未知数换成了某个常数，那么这样的方程可以直接得解，请用这个结论解关于x的方程： $\text{[math]}$ 。
答案解析收藏纠错 + 选题
6. (2018七上·惠来月考) 解方程
1. （1） 3x-2=1-2（x+1）
2. （2） $\text{[math]}$
3. （3） 2x+3（2x﹣1）=16-（x+1）
4. （4） $\text{[math]}$
答案解析收藏纠错 + 选题
7. (2018七上·黑龙江期末) 我市为迎接省运会，要将某一城市美化工程招标，有甲、乙两个工程队投标，经测算：甲队单独完成这项工程需要60天，若由甲队先做20天，剩下的工程由甲、乙合作24天可完成．
1. （1）乙队单独完成这项工程需要多少天？
2. （2）甲队施工一天，需付工程款3.5万元，乙队施工一天需付工程款2万元．若该工程计划在70天内完成，在不超过计划天数的前提下，是由甲队或乙队单独完成工程省钱？还是由甲乙两队全程合作完成该工程省钱？
答案解析收藏纠错 + 选题
8. (2016七上·长兴期末)
某学校校门口有一个长为9m的长条形（长方形）电子显示屏，学校的有关活动都会在“电子显示屏”播出，由于各次活动的名称不同，字数也就不等，为了制作及显示时方便美观，负责播出的老师对有关数据作出了如下规定：若字数在8个以下，边空：字宽：字距=2：4：1；若字数在8个以上（含8个），边空：字宽：字距=2：3：1，如图所录：
1. （1）某次活动的字数为9个，求字距是多少？
2. （2）如果某次活动的字宽为36cm，问字数是多少个？
答案解析收藏纠错 + 选题
9. 在数学学习过程中，通常是利用已有的知识与经验，通过对研究对象进行观察、实验、推理、抽象概括，发现数学规律，揭示研究对象的本质特征．
比如“同底数幂的乘法法则”的学习过程是利用有理数的乘方概念和乘法结合律，由“特殊”到“一般”进行抽象概括的：
2²×2³=2⁵ ， 2³×2⁴=2⁷ ， 2²×2⁶=2⁸…⇒2^m×2ⁿ=2^m+n…⇒a^m×aⁿ=a^m+n（m、n都是正整数）．
我们亦知： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ …
1. （1）请你根据上面的材料，用字母a、b、c归纳出a、b、c（a＞b＞0，c＞0）之间的一个数学关系式．
2. （2）试用（1）中你归纳的数学关系式，解释下面生活中的一个现象：“若m克糖水里含有n克糖，再加入k克糖（仍不饱和），则糖水更甜了”．
答案解析收藏纠错 + 选题
10. (2020七下·萧山期中)
1. （1）分解因式：2mx²﹣4mxy+2my².
2. （2）先化简，再求值： $\text{[math]}$ ，其中x=2020.
答案解析收藏纠错 + 选题
11. (2020七下·余姚月考) 某幼儿园计划购进一批甲、乙两种玩具，已知一件甲种玩具的价格与一件乙种玩具的价格的和为40元，用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
1. （1）求每件甲种、乙种玩具的价格分别是多少元？
2. （2）该幼儿园计划用3500元购买甲、乙两种玩具，由于采购人员把甲、乙两种玩具的件数互换了，结果需4500元，求该幼儿园原计划购进甲、乙两种玩具各多少件？
答案解析收藏纠错 + 选题
12. (2021七上·乾安期末) 有一些相同的房间需要粉刷，一天3名师傅去粉刷8个房间，结果其中有40m²墙面未来得及刷；同样的时间内5名徒弟粉刷了9个房间的墙面．每名师傅比徒弟一天多刷30m²的墙面．
1. （1）求每个房间需要粉刷的墙面面积；
2. （2）张老板现有36个这样的房间需要粉刷，若请1名师傅带2名徒弟去，需要几天完成．
答案解析收藏纠错 + 选题
13. (2020七上·洪山期末) 用分式方程解决问题：元旦假期有两个小组去攀登一座高h米的山，第二组的攀登速度是第一组的a倍.
1. （1）若 $\text{[math]}$ ，两小组同时开始攀登，结果第二组比第一组早 $\text{[math]}$ 到达顶峰.求两个小组的攀登速度.
2. （2）若第二组比第一组晚出发 $\text{[math]}$ ，结果两组同时到达顶峰，求第二组的攀登速度比第一组快多少?(用含 $\text{[math]}$ 的代数式表示)
答案解析收藏纠错 + 选题
14. (2021·黄石模拟) 一个批发兼零售的文具店规定：凡一次购买铅笔300枝以上，（不包括300枝），可以按批发价付款，购买300枝以下，（包括300枝）只能按零售价付款．小明来该店购买铅笔，如果给八年级学生每人购买1枝，那么只能按零售价付款，需用120元，如果购买60枝，那么可以按批发价付款，同样需要120元，
1. （1）这个八年级的学生总数在什么范围内？
2. （2）若按批发价购买6枝与按零售价购买5枝的款相同，那么这个学校八年级学生有多少人？
答案解析收藏纠错 + 选题
15. (2019七上·杨浦月考) 某公司开发生产960件新产品，需要加工后才能投放市场，现甲、乙两个工厂都想加工这批产品，已知甲工厂单独完成这批产品比乙工厂单独完成这批产品多用20天，而乙工厂每天加工的件数是甲工厂每天加工件数的1.5倍，公司需付甲工厂加工费每天80元，乙工厂每天加工费用120元。
1. （1）求甲、乙两个工厂每天各能加工多少个新产品?
2. （2）公司制定产品加工方案如下:可以由每个厂家单独完成，也可以由两个厂家同时合作完成。在加工过程中，公司派一名工程师每天来厂进行技术指导，并负担每天5元的午餐补助费，请你帮助公司选择一种既省时又省力的方案，并说明理由。
答案解析收藏纠错 + 选题
16. (2019七上·柯桥期中) 如图，为建设美丽农村，村委会打算在正方形地块甲和长方形地块乙上进行绿化.在两地块内分别建造一个边长为a的大正方形花坛和四个边长为b的小正方形花坛(阴影部分)，空白区域铺设草坪，记S₁表示地块甲中空白处铺设草坪的面积，S₂表示地块乙中空白处铺设草坪的面积．
1. （1） S₁=，S₂=(用含a，b的代数式表示并化简) .
2. （2）若a=2b，求的 $\text{[math]}$ 值
答案解析收藏纠错 + 选题
17. (2019七下·南浔期末) 南浔区某校组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动，基地离学校有120千米，队伍乘大巴车8：00从学校出发.苏老师因有事情，8：30从学校自驾小汽车以大巴车1.5倍的速度追赶，追上大巴车后继续前行，结果比队伍提前10分钟到达基地.问：
1. （1）设大巴午的平均速度是x(km／h)，利用速度、时间和路程之间的关系填写下表.(要求：填上适当的代数式，完成表格)(温馨提示：请填写在答题卷相对应的表格内)
  
  速度（km/h）
  
  路程（km）
  
  时间（h）
  
  大巴车
  
  x
  
  120
  
  小汽车
  
  120
2. （2）列出方程，并求出大巴车与小汽车的平均速度.
3. （3）当苏老师追上大巴车时，大巴车离基地还有多远?
答案解析收藏纠错 + 选题
18. (2019七下·嘉兴期末) 某服装店购进一批甲、乙两种款型的时尚T恤衫，甲种款型共用了7800元，乙种款型共用了6 400元，甲种款型的件数是乙种款型件数的1.5倍，甲种款型每件的进价比乙种款型每件的进价少30元
1. （1）甲、乙两种款型的T恤衫各购进多少件?
2. （2）商店按进价提高60％标价销售，销售一段时间后，甲款型全部售完，乙款型剩余一半，商店决定对乙款型按标价的五折销售，很快全部售完.求售完这批T恤衫商店共获利多少元?
答案解析收藏纠错 + 选题
19. (2019七下·余杭期末) 为改善生态环境，促进国土绿化，某市甲、乙两支志愿者队伍分别参加了两地的植树活动．
1. （1）甲队在A地植树，如果每人种4棵，还剩下66棵树苗；如果每人种5棵，则缺少30棵树苗．求甲队志愿者的人数和A地需种植的树苗数．
2. （2）乙队在B地植树，原计划植树1200棵，由于另有新加入的志愿者共同参与植树，每日比原计划多种 $\text{[math]}$ ，结果提前2天完成任务．问原计划每天植树多少棵?
答案解析收藏纠错 + 选题
20. (2019七下·西湖期末) 一项工程甲队单独完成所需天数是乙队单独完成这项工程所需天数的 $\text{[math]}$ ；若由乙队先做45天，剩下的工程再由甲、乙两队合作54天可以完成。
1. （1）求甲、乙两队单独完成这项工程各需要多少天？
2. （2）已知甲队每天的施工费用为0.82万元，乙队每天的施工费用为0.68万元，工程预算的施工费用为100万元.拟安排甲、乙两队同时合作完成这项工程，则工程预算的施工费用是否够用？若不够用，需追加预算多少万元？说明理由.
答案解析收藏纠错 + 选题
21. (2019七下·衢州期末) 某商家预测一种应季衬衫能畅销市场，就用13200元购进了一批这种衬衫，面市后果然供不应求，商家又用28800元购进了第二批这种衬衫，所购数量是第一批购进量的2倍，但单价贵了10元．
1. （1）该商家购进的第一批衬衫是多少件?
2. （2）若两批衬衫按相同的标价150元销售，最后剩下50件按八折优惠卖出，求两批衬衫全部售完后利润是多少元?
答案解析收藏纠错 + 选题
22. (2019七下·长兴期末) 某市为创建生态文明城市，对公路旁的绿化带进行全面改造．现有甲、乙两个工程队，有三种施工方案：
方案一：甲队单独完成这项工程，刚好能如期完成；

方案二：乙队单独完成这项工程，要比预定工期多用3天；

方案三：先由甲、乙两队一起合作2天，剩下的工程由乙队单独完成，刚好如期完成。
1. （1）求工程预定工期的天数
2. （2）若甲队每施工一天需工程款2万元，乙队每施工一天需工程款1.3万元．为节省工程款，同时又如期完工，请你选择一种方案，并说明理由
答案解析收藏纠错 + 选题
23. (2018七下·余姚期末) 某工厂承接了一批纸箱加工任务，用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)作侧面和底面，加工成如图2所示的竖式和横式两种无盖的长方体纸箱.(加工时接缝材料不计)
1. （1）若该厂仓库里有1000张正方形纸板和2000张长方形纸板.问竖式和横式纸箱各加工多少个，恰好将库存的两种纸板全部用完?
2. （2）该工厂原计划用若干天加工纸箱2400个，后来由于对方急需要货，实际加工时每天加工速度是原计划的1.5倍，这样提前2天完成了任务，问原计划每天加工纸箱多少个?
答案解析收藏纠错 + 选题
24. (2019七下·陆川期末) 计算或解方程：
1. （1）计算(-1)²⁰¹⁶- $\text{[math]}$ +| $\text{[math]}$ |
2. （2）解方程组 $\text{[math]}$
3. （3）解方程组 $\text{[math]}$
4. （4）解不等式 $\text{[math]}$ ，并把解集表示在数轴上
答案解析收藏纠错 + 选题
25. (2019七下·永康期末) 先阅读下面的材料，然后回答问题：
方程 $\text{[math]}$ 的解为 $\text{[math]}$ ， $\text{[math]}$ ；

方程 $\text{[math]}$ 的解为 $\text{[math]}$ ， $\text{[math]}$ ；

方程 $\text{[math]}$ 的解为 $\text{[math]}$ ， $\text{[math]}$ ； …
1. （1）观察上述方程的解，猜想关于x的方程 $\text{[math]}$ 的解是；
2. （2）根据上面的规律，猜想关于x的方程 $\text{[math]}$ 的解是；
3. （3）猜想关于x的方程x− $\text{[math]}$ 的解并验证你的结论；
4. （4）在解方程： $\text{[math]}$ 时，可将方程变形转化为(2)的形式求解，按要求写出你的变形求解过程。
答案解析收藏纠错 + 选题

试卷信息