北京市朝阳区2022年中考数学模拟试题

更新时间：2024-07-13 浏览次数：147 类型：中考模拟

一、单选题

1. (2022·朝阳模拟) 在国内疫情持续好转、旅游产业复工复产的当下，迎来了2020中秋国庆黄金周．据统计，本次黄金周全国出游人数约为637000000人次．把数据637000000用科学记数法表示为（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022九上·广宗期末) 如图，是一个由多个相同小正方体堆积而成的几何体的俯视图，图中所示数字为该位置小正方体的个数，则这个几何体的主视图（从正面看）是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022·朝阳模拟) 如图，将一条两边沿互相平行的纸带按图折叠，则∠1的度数等于（）

A . 65° B . 70° C . 75° D . 80°

答案解析收藏纠错 + 选题
4. (2024·惠东模拟) 下列几何图形中，既是中心对称图形又是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2022·朝阳模拟) 正方形 $\text{[math]}$ 在数轴上的位置如图所示，点 $\text{[math]}$ ， $\text{[math]}$ 对应的数分别为-1和0，若正方形 $\text{[math]}$ 绕着顶点顺时针方向在数轴上连续翻转，翻转1次后，点 $\text{[math]}$ 所对应的数为1；翻转2次后，点 $\text{[math]}$ 所对应的数为2；翻转3次后，点 $\text{[math]}$ 所对应的数为3；翻转4次后，点 $\text{[math]}$ 所对应的数为4，…，则连续翻转2019次后，数轴上数2019所对应的点是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·朝阳模拟) 一个不透明的袋子中装有1个红球，2个绿球，除颜色外无其他差别，从中随机摸出一个球，然后放回摇匀，再随机摸出一个．给出下列结论：①第一次摸出的球是红球，第二次摸出的球一定是绿球；②第一次摸出的球是红球，第二次摸出的球不一定是绿球；③第一次摸出的球是红球的概率是 $\text{[math]}$ ；④两次摸出的球都是红球的概率是 $\text{[math]}$ ．其中正确的结论个数为（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
7. (2022·朝阳模拟) 一元二次方程x²+5x+3=0的根的情况是（　　）

A . 有两个相等的实数根 B . 有两个不相等的实数根 C . 没有实数根 D . 无法确定

答案解析收藏纠错 + 选题
8. (2022·朝阳模拟) 已知张强家、体育场、文具店在同一直线上.如图的图象反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后又走到文具店去买笔，然后散步走回家．图中x表示时间，y表示张强离家的距离．则下列说法不正确的是（）

A . 体育场离张强家2.5千米 B . 体育场离文具店1千米 C . 张强在文具店逗留了15分钟 D . 张强从文具店回家的平均速度是 $\text{[math]}$ 千米/分

答案解析收藏纠错 + 选题

二、填空题

9. (2023八下·河东期中) 二次根式 $\text{[math]}$ 中字母 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
10. (2024·惠东模拟) 估算 $\text{[math]}$ ≈．（精确到0.1）

答案解析收藏纠错 + 选题
11. (2022·朝阳模拟) 如果：□+□+△=14，□+□+△+△+△=30，则□=.

答案解析收藏纠错 + 选题
12. (2022·朝阳模拟) 圆心角为90°，半径为6cm的扇形的弧长是cm（结果保留π）．

答案解析收藏纠错 + 选题
13. (2024九上·银州期末) 如图，∠A＝∠B＝90°，AB＝7，AD＝2，BC＝3，在边AB上取点P，使得△PAD与△PBC相似，则满足条件的AP长.

答案解析收藏纠错 + 选题
14. (2022·朝阳模拟) 抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ， $\text{[math]}$ 两点，则不等式 $\text{[math]}$ 的解集是.

答案解析收藏纠错 + 选题
15. (2022·朝阳模拟) 已知如图，在 $\text{[math]}$ ABC中， $\text{[math]}$ BAE= $\text{[math]}$ CAE，BE $\text{[math]}$ AE于点E，若 $\text{[math]}$ ABC=3 $\text{[math]}$ ACB，则AB，AC，BE之间的数量关系．

答案解析收藏纠错 + 选题

16. (2022·朝阳模拟) 在一段时间内，小军骑自行车上学和乘坐公共汽车上学的次数基本相同，他随机记录了其中某些天上学所用的时间，整理如表：

交通工具	所需时间（单位：min）
自行车	14，14，14，15，15，15，15，15，15，15，15，15，15，15，15
公共汽车	10，10，11，11，11，12，12，12，12，13，15，16，17，17，19

下面有四个推断：

①平均来说，乘坐公共汽车上学所需的时间较短

②骑自行车上学所需的时间比较容易预计

③如果小军想在上学路上花的时间更少，他应该更多地乘坐公共汽车

④如果小军一定要在16min内到达学校，他应该乘坐公共汽车

其中合理的是（填序号）．

答案解析收藏纠错 + 选题

三、解答题

17. (2022·朝阳模拟) 计算：（﹣1）²⁰²⁰﹣ $\text{[math]}$ ﹣（3﹣π）⁰+|3﹣ $\text{[math]}$ |+（tan30°）^﹣¹ ．

答案解析收藏纠错 + 选题
18. (2021八下·文山期末) 解不等式组 $\text{[math]}$

答案解析收藏纠错 + 选题
19. (2022·朝阳模拟) 解方程：1﹣ $\text{[math]}$ ＝ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2022·朝阳模拟) 先化简，再求值：（2a+1）²﹣2（a+2）（a﹣2），其中a为方程2x²+4x﹣3＝0的解．

答案解析收藏纠错 + 选题
21. (2024九上·扶余期末) 已知：如图， $\text{[math]}$ ABC为锐角三角形，AB=AC，CD∥AB．
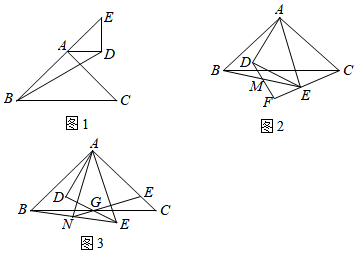
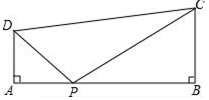
求作：线段BP，使得点P在直线CD上，且∠ABP= $\text{[math]}$ ．
作法：①以点A为圆心，AC长为半径画圆，交直线CD于C，P两点；②连接BP．线段BP就是所求作线段．
1. （1）使用直尺和圆规，依作法补全图形（保留作图痕迹）
2. （2）完成下面的证明．
  证明：∵CD∥AB，
  ∴∠ABP= ▲ ．
  ∵AB=AC，
  ∴点B在⊙A上．
  又∵∠BPC= $\text{[math]}$ ∠BAC（）（填推理依据）
  ∴∠ABP= $\text{[math]}$ ∠BAC
答案解析收藏纠错 + 选题
22. (2022·朝阳模拟) 如图，在矩形 ABCD中，AD=10，tan $\text{[math]}$ AEB= $\text{[math]}$ ，点E为BC 上的一点，ED平分 $\text{[math]}$ AEC，
1. （1）求BE的值；
2. （2）求sin $\text{[math]}$ EDC．
答案解析收藏纠错 + 选题
23. (2022·朝阳模拟) 已知：一次函数y₁＝x﹣2﹣k与反比例函数y₂＝ $\text{[math]}$ （k≠0）．
1. （1）当k＝1时，
  ①求出两个函数图象的交点坐标；
  ②根据图象回答：x取何值时，y₁＜y₂；
2. （2）请说明：当k取任何不为0的值时，两个函数图象总有交点；
3. （3）若两个函数图象有两个不同的交点A、B，且AB＝5 $\text{[math]}$ ，求k值．
答案解析收藏纠错 + 选题
24. (2022·朝阳模拟) 如图，AB为⊙O的直径，点C在⊙O上，点P是直径AB上的一点，（不与A，B重合），过点P作AB的垂线交BC的延长线于点Q，与AC相交于点M，CD是⊙O的切线．
1. （1）求证：∠Q＝∠DCQ；
2. （2）若sin∠Q＝ $\text{[math]}$ ， AP＝4，MC＝6，求PB的长．
答案解析收藏纠错 + 选题
25. (2022·朝阳模拟) 某地农业科技部门积极助力家乡农产品的改良与推广，为了解甲、乙两种新品橙子的质量，进行了抽样调查．在相同条件下，随机抽取了甲、乙各25份样品，对大小、甜度等各方面进行了综合测评，并对数据进行收集、整理、描述和分析，下面给出了部分信息．
a．测评分数（百分制）如下：

甲77 79 80 80 85 86 86 87 88 89 89 90 91 91 91 91 91

92 93 95 95 96 97 98 98

乙69 79 79 79 86 87 87 89 89 90 90 90 90 90 91 92 92

92 94 95 96 96 97 98 98

b．按如下分组整理、描述这两组样本数据：

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

甲

0

2

9

14

乙

1

3

5

16

c．甲、乙两种橙子测评分数的平均数、众数、中位数如下表所示：

品种

平均数

众数

中位数

甲

89.4

m

91

乙

89.4

90

n

根据以上信息，回答下列问题：
1. （1）写出表中 $\text{[math]}$ 的值；
2. （2）记甲种橙子测评分数的方差为 $\text{[math]}$ ，乙种橙子测评分数的方差为 $\text{[math]}$ ，则 $\text{[math]}$ 的大小关系为；
3. （3）根据抽样调查情况，可以推断种橙子的质量较好，理由为．
  （至少从两个不同的角度说明推断的合理性）
答案解析收藏纠错 + 选题
26. (2022·朝阳模拟) 已知等腰直角△ABC中，∠BAC＝90°，AB＝AC，以A为顶点作等腰直角△ADE，其中AD＝DE．
1. （1）如图1，点E在BA的延长线上，连接BD，若∠DBC＝30°，若AB＝6，求BD的值；
2. （2）将等腰直角△ADE绕点A顺时针旋转至图2，连接BE，CE，过点D作DF⊥CE交CE的延长线于F，交BE于M，求证：BM＝ $\text{[math]}$ BE；
3. （3）如图3，等腰直角△ADE的边长和位置发生变化的过程中，DE边始终经过BC的中点G，连接BE，N为BE中点，连接AN，当AB＝6且AN最长时，连接NG并延长交AC于点K，请直接写出△ANK的面积．
答案解析收藏纠错 + 选题
27. (2022·朝阳模拟) 已知函数 $\text{[math]}$ （b ， c为常数）的图象经过点 $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ 时，求抛物线的顶点坐标；
2. （2）设该函数图象的顶点坐标是 $\text{[math]}$ ，当b的值变化时，求n关于m的函数解析式；
3. （3）若该函数的图象不经过第三象限，当 $\text{[math]}$ 时，函数的最大值与最小值之差为40，求b的值．
答案解析收藏纠错 + 选题
28. (2022·朝阳模拟) 如图①，Rt $\text{[math]}$ ABC和Rt $\text{[math]}$ BDE重叠放置在一起，∠ABC＝∠DBE＝90°，且AB＝2BC，BD＝2BE．
1. （1）观察猜想：图①中线段AD与CE的数量关系是，位置关系是；
2. （2）探究证明：把 $\text{[math]}$ BDE绕点B顺时针旋转到图②的位置，连接AD，CE，判断线段AD与CE的数量关系和位置关系如何，并说明理由；
3. （3）拓展延伸：若BC＝ $\text{[math]}$ ， BE＝1，当旋转角α＝∠ACB时，请直接写出线段AD的长度．
答案解析收藏纠错 + 选题