B .
B .  C .
C .  D .
D . 




类别 | 频数(人数) | 频率 |
力学 | 0.5 | |
热学 | 8 | |
光学 | 20 | 0.25 |
电学 | 12 |

如图2,电路图上有四个开关A,B,C,D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光,若随机闭合其中的两个开关,用画树状图或列表的方法求小灯泡发光的概率.

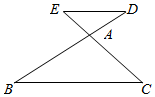
已知:如图1,P是外一点, ▲ .
求证: ▲ .
每袋的售价x(元) | … | 20 | 30 | … |
日销售量y(袋) | … | 20 | 10 | … |
如果日销售量y(袋)是每袋的售价x(元)的一次函数,请回答下列问题: