北师大版备考2022中考数学二轮复习专题19 多边形与平行四...

更新时间：2022-04-20 浏览次数：209 类型：二轮复习

一、单选题

1. (2019八上·吉木乃月考) 如图，五边形ABCDE的每一个内角都相等，则外角∠CBF等于（）

A . 60° B . 72° C . 80° D . 108°

答案解析收藏纠错 + 选题
2. (2022九下·温州开学考) 如图，在Rt△ABC中，∠ACB＝90°，以其三边为边向外作正方形，过点C作CI⊥HJ于点I，交AB于K，在图形的外部作矩形MNPQ，使点D，E，G和H，J都落在矩形的边上.已知矩形BJIK的面积为1，正方形ACDE的面积为4，则 $\text{[math]}$ 为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021八上·剑河月考) 一个多边形除一个内角外其余内角的和为1510°，则这个多边形对角线的条数是（　　）

A . 27 B . 35 C . 44 D . 54

答案解析收藏纠错 + 选题
4.
如图，在平行四边形ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是（　　）
①∠DCF= $\text{[math]}$ ∠BCD；②EF=CF；③S_△_BEC=2S_△_CEF；④∠DFE=3∠AEF．

A . ①② B . ②③④ C . ①②④ D . ①②③④

答案解析收藏纠错 + 选题
5. (2019·广西模拟) 如图，在五边形ABCDE中，∠A+∠B+∠E=∠EDC+∠BCD+140°，DF，CF分别平分∠EDC和∠BCD，则∠F的度数为（　　）

A . 100° B . 90° C . 80° D . 70°

答案解析收藏纠错 + 选题
6. (2022八下·灌阳期中)
如图，在四边形ABCD中，AB∥DC，AD=BC=5，DC=7，AB=13，点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动，同时点Q从点B出发，以1个单位/s的速度沿BA向终点A运动．当四边形PQBC为平行四边形时，运动时间为（　　）

A . 4s B . 3s C . 2s D . 1s

答案解析收藏纠错 + 选题
7.
如图，在平面直角坐标系中，以O（0，0）、A（1，-1）、B（2，0）为顶点，构造平行四边形，下列各点中不能作为平行四边形第四个顶点坐标的是（　　　）

A . （3，-1） B . （-1，-1） C . （1，1） D . （-2，-1）

答案解析收藏纠错 + 选题
8. (2021八上·肇源期末) 如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°， $\text{[math]}$ ，则下列结论：①∠CAD=30° ② $\text{[math]}$ ③S_{平行四边形ABCD}=AB•AC ④ $\text{[math]}$ ，正确的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
9. (2022·南海模拟) 如图，正方形ABCD中，点E是边CD上的动点（不与点C、D重合），以CE为边向右作正方形CEFG，连接AF，点H是AF的中点，连接DH、CH．下列结论：①△ADH≌△CDH；②AF平分∠DFE；③若BC＝4，CG＝3，则AF＝5；④若 $\text{[math]}$ ，则 $\text{[math]}$ ．其中正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
10. 如图，矩形ABCD的面积为1cm² ，对角线交于点O；以AB、AO为邻边作平行四边形AOC₁B，对角线交于点O₁；以AB、AO₁为邻边作平行四边形AO₁C₂B…；依此类推，则平行四边形AO₂₀₁₄C₂₀₁₅B的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2021八下·历下期末) 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的周长是.

答案解析收藏纠错 + 选题
12.
如图，已知四边形ABCD中，∠C=72°，∠D=81°．沿EF折叠四边形，使点A、B分别落在四边形内部的点A′、B′处，则∠1+∠2=°．

答案解析收藏纠错 + 选题
13.
如图，▱ABCD中，AB＞AD，AE，BE，CM，DM分别为∠DAB，∠ABC，∠BCD，∠CDA的平分线，AE与DM相交于点F，BE与CM相交于点N，连接EM．若▱ABCD的周长为42cm，FM=3cm，EF=4cm，则EM= cm，AB= cm．

答案解析收藏纠错 + 选题
14.
如图，平行四边形ABCD绕点A逆时针旋转30°，得到平行四边形AB′C′D′（点B′与点B是对应点，点C′与点C是对应点，点D′与点D是对应点），点B′恰好落在BC边上，则∠C=

答案解析收藏纠错 + 选题
15. (2023·梅州模拟)
如图，在▱ABCD中，AD=2，AB=4，∠A=30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是（结果保留π）.

答案解析收藏纠错 + 选题
16. 如图，已知▱OABC的顶点A、C分别在直线x=1和x=4上，O是坐标原点，则对角线OB长的最小值为．

答案解析收藏纠错 + 选题
17. 如图，菱形ABC的对角线相交于点O，过点D作DE∥AC，且DE= $\text{[math]}$ AC，连接CE、OE、AE，AE交OD于点F，若AB=2，∠ABC=60°，则AE的长．

答案解析收藏纠错 + 选题
18. (2020八下·漯河期中)
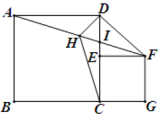
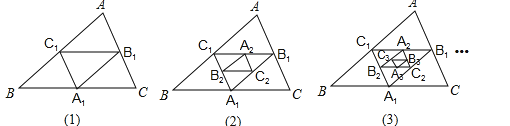
如图，在图（1）中，A₁、B₁、C₁分别是△ABC的边BC、CA、AB的中点，在图（2）中，A₂、B₂、C₂分别是△A₁B₁C₁的边B₁C₁、C₁A₁、A₁B₁的中点，…，按此规律，则第n个图形中平行四边形的个数共有个

答案解析收藏纠错 + 选题

三、作图题

19. (2019九上·海淀期中) 已知∠MON=α，P为射线OM上的点，OP=1．
1. （1）如图1，α=60°，A，B均为射线ON上的点，OA=1，OB＞OA，△PBC为等边三角形，且O，C两点位于直线PB的异侧，连接AC．
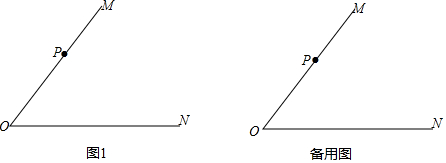
  ①依题意将图1补全；
  
  ②判断直线AC与OM的位置关系并加以证明；
2. （2）若α=45°，Q为射线ON上一动点（Q与O不重合），以PQ为斜边作等腰直角△PQR，使O，R两点位于直线PQ的异侧，连接OR．根据（1）的解答经验，直接写出△POR的面积．
答案解析收藏纠错 + 选题

四、综合题

20.
如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．
1. （1）试说明AC=EF；
2. （2）求证：四边形ADFE是平行四边形.
答案解析收藏纠错 + 选题
21. (2021八上·南阳期末) 如图，平行四边形ABCO位于直角坐标系中，O为坐标原点，点 $\text{[math]}$ ，点 $\text{[math]}$ 交y轴于点 $\text{[math]}$ 动点E从点D出发，沿DB方向以每秒1个单位长度的速度终点B运动，同时动点F从点A出发，沿射线OA的方向以每秒2个单位长度的速度运动，当点E运动到点B时，点F随之停止运动，运动时间为 $\text{[math]}$ 秒 $\text{[math]}$ .
1. （1）用t的代数式表示： $\text{[math]}$ ， $\text{[math]}$
2. （2）若以A，B，E，F为顶点的四边形是平行四边形时，求t的值.
3. （3）当 $\text{[math]}$ 恰好是等腰三角形时，求t的值.
答案解析收藏纠错 + 选题
22. (2019九上·黑龙江期末) 如图，矩形OABC在平面直角坐标系中，若x²-2 $\text{[math]}$ x+2=0的两根是x₁、x₂ ，且OC=x₁+x₂ ， OA=x₁x₂
1. （1）求B点的坐标.
2. （2）把△ABC沿AC对折，点B落在点B′处，线段AB′与x轴交于点D，求直线BD的解析式．
3. （3）在平面上是否存在点P，使D、C、B、P四点形成的四边形为平形四边形？若存在，请直接写出P 点坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题
23. (2017·海南)
如图，四边形ABCD是边长为1的正方形，点E在AD边上运动，且不与点A和点D重合，连结CE，过点C作CF⊥CE交AB的延长线于点F，EF交BC于点G．
1. （1）求证：△CDE≌△CBF；
2. （2）当DE= $\text{[math]}$ 时，求CG的长；
3. （3）连结AG，在点E运动过程中，四边形CEAG能否为平行四边形？若能，求出此时DE的长；若不能，说明理由．
答案解析收藏纠错 + 选题