四川省广元市2022年中考数学模拟试题

更新时间：2024-07-13 浏览次数：50 类型：中考模拟

一、单选题

1. (2022·广元模拟) 若有理数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 6 B . 8 C . 4 D . 4或8

答案解析收藏纠错 + 选题
2. (2024·惠东模拟) 下列几何图形中，既是中心对称图形又是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. 下列运算正确的是（）

A . 4a-a=3 B . 2(2a-b)=4a-b C . (a+b)²=a²+b² D . (a+2)(a-2)=a²-4

答案解析收藏纠错 + 选题
4. (2024九上·朝阳开学考) 一组数据：1、2、2、3，若添加一个数据2，则发生变化的统计量是（）

A . 平均数 B . 中位数 C . 众数 D . 方差

答案解析收藏纠错 + 选题
5. (2022·广元模拟) 下列命题正确的是（）

A . 对角线互相垂直的平行四边形是菱形 B . 有一个角是直角的四边形是矩形 C . 有一组对角相等的四边形是平行四边形 D . 对角线互相垂直且相等的四边形是正方形

答案解析收藏纠错 + 选题
6. (2022·广元模拟) 用三角板作 $\text{[math]}$ 的边 $\text{[math]}$ 上的高，下列三角板的摆放位置正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2022·广元模拟) 圆锥的底面半径为1，母线长为3，则该圆锥侧面积为（）

A . 3 B . 6π C . 3π D . 6

答案解析收藏纠错 + 选题
8. (2022·广元模拟) 已知二次函数y=﹣x²+x+6及一次函数y=﹣x+m，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新函数（如图所示），请你在图中画出这个新图象，当直线y=﹣x+m与新图象有4个交点时，m的取值范围是（）

A . ﹣ $\text{[math]}$ ＜m＜3 B . ﹣ $\text{[math]}$ ＜m＜2 C . ﹣2＜m＜3 D . ﹣6＜m＜﹣2

答案解析收藏纠错 + 选题
9. (2023·信宜模拟) 如图，正方形的四个顶点在半径为 2 的大圆圆周上，四条边都与小圆都相切， $\text{[math]}$ 过圆心 $\text{[math]}$ ，且 $\text{[math]}$ ，则图中阴影部分的面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022·广元模拟) 如图所示，△ACB中，∠ACB＝90°，CD⊥AB于D，则下列结论：①BC＞CD；②AC＞AD；③AB＞AC；④BC＞AD．正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

11. (2022·广元模拟) 计算： $\text{[math]}$ ＝．

答案解析收藏纠错 + 选题
12. (2022·广元模拟) 已知点A在数轴上，且和表示1的点相距 $\text{[math]}$ 个单位长度，则点A表示的数为．

答案解析收藏纠错 + 选题
13. (2022·广元模拟) 如图，点A，B，C在同一个圆上，∠ACB＜90°，弦AB的长度等于该圆半径的 $\text{[math]}$ 倍，则cos∠ACB的值是.

答案解析收藏纠错 + 选题
14. (2022·广元模拟) 如图，在△ABC中，AB＝AC，点A在y轴上，点C在x轴上，BC⊥x轴，tan∠ACO＝ $\text{[math]}$ ．延长AC到点D，过点D作DE⊥x轴于点G，且DG＝GE，连接CE，反比例函数y＝ $\text{[math]}$ （k≠0）的图象经过点B，和CE交于点F，且CF：FE＝2：1．若△ABE面积为6，则点D的坐标为．

答案解析收藏纠错 + 选题
15. (2022八下·封开期末) 如图，直线 $\text{[math]}$ 过正方形 $\text{[math]}$ 的顶点 $\text{[math]}$ ，点 $\text{[math]}$ 到直线 $\text{[math]}$ 的距离分别是 $\text{[math]}$ 和 $\text{[math]}$ ，且满足： $\text{[math]}$ ，则正方形 $\text{[math]}$ 的面积是．

答案解析收藏纠错 + 选题

三、解答题

16. (2022·广元模拟) 解方程： $\text{[math]}$

答案解析收藏纠错 + 选题
17. (2022·广元模拟) 先化简，再求值：（1 $\text{[math]}$ ） $\text{[math]}$ ，其中x $\text{[math]}$ 1．

答案解析收藏纠错 + 选题
18. (2022·广元模拟) 如图，在平行四边形ABCD中，连接对角线AC，延长AB至E，使BE＝AB，连接DE，分别交BC，AC于点F，G．
1. （1）求证：BF＝CF；
2. （2）若BC＝6，DG＝4，求FG的长；
3. （3）若△FCG面积为1，则四边形ABFG面积为多少？
答案解析收藏纠错 + 选题
19. (2022·广元模拟) 某汽车配件厂生产甲、乙、丙三种汽车轮胎．生产各种轮胎所需的工时和产值如下表所示，又知道每周生产三种轮胎的总工时是168个，总产值是111.2万元
汽车零部件
甲种
乙种
丙种
每个所需工时（个）
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
每个产值（千元）
4
3
1
1. （1）若每周丙种轮胎生产252台，问其它两种轮胎每周分别生产多少个？
2. （2）现有4S店以产值价的1.2倍购进这三种轮胎共100个，考虑市场需求和资金周转，其中丙种轮胎购进50个，而用于购买这100个轮胎的总资金最少24.96万元，但最多不超过25.2万元，那么该商店有哪几种购进轮胎方案？
3. （3）若销售每件甲种轮胎可获利200元，每件乙种轮胎可获利150元，每件丙种轮胎可获利100元，在第（2）问的进货方案中，哪一种方案获利最大？最大利润是多少元？
答案解析收藏纠错 + 选题

20. (2022·广元模拟) 在初三年级某班的一次体育模拟测试中，班长对全班同学的测试成绩进行了统计，并绘制了如下不完整的统计图表，请根据图表提供的信息完成以下问题：

组别	成绩	人数
A	90≤x<100	4
B	80≤x<90	15
C	70≤x<80	m
D	60≤x<70	10

（1）图表中：m＝；B组的圆心角为度．
（2） A组4名同学中有2男2女，从中随机抽取两名同学参加市运会，请你用画树状图或列表法求：
①被抽取的2名同学恰好是1男1女的概率；
②至少1名男生被抽到的概率．

答案解析收藏纠错 + 选题

21. (2022·广元模拟) 2019年12月27日，我国成功发射了“长征五号”遥三运载火箭.如图，“长征五号”运载火箭从地面 $\text{[math]}$ 处垂直向上发射，当火箭到达 $\text{[math]}$ 处时，从位于地面 $\text{[math]}$ 处的雷达站测得此时仰角 $\text{[math]}$ ，当火箭继续升空到达 $\text{[math]}$ 处时，从位于地面 $\text{[math]}$ 处的雷达站测得此时仰角 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的长；
2. （2）若“长征五号”运载火箭在 $\text{[math]}$ 处进行“程序转弯”，且 $\text{[math]}$ ，求雷达站 $\text{[math]}$ 到其正上方点 $\text{[math]}$ 的距离.
答案解析收藏纠错 + 选题
22. (2022·广元模拟) 点A（﹣3，1），B（﹣2，2），反比例函数y＝ $\text{[math]}$ （k＜0，x＜0）的图象记为L ．
1. （1）若L经过点A ．
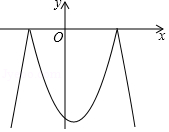
  ①图象L的解析式为 ▲ ．
  
  ②点B在图象L上，还是在图象L的上方或下方？为什么？
2. （2）如图在（1）的条件下，L上纵坐标为3的点P与点C关于原点O对称，PQ⊥x轴于点Q ， CD⊥x轴于点D ．求△QCD的面积．
3. （3）若L与线段AB有公共点，直接写出k的取值范围．
答案解析收藏纠错 + 选题
23. (2022·广元模拟) 已知：如图所示，MN是⊙O的直径，B是⊙O上一点，NP平分∠BNM交⊙O于P，过P作PA⊥BN于A．
1. （1）求证：PA与⊙O相切；
2. （2）若MN＝20，BN＝12，求MP的长；
3. （3）若D是ON中点，过D作CD⊥ON交AP于C，若CD＝19，tan∠MNP＝ $\text{[math]}$ ，求⊙O的半径．
答案解析收藏纠错 + 选题
24. (2022八上·镇海区期中) 从三角形（不是等腰三角形）一个顶点引出的一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形有两角对应相等，我们把这条线段叫做这个三角形的“优美分割线”.
1. （1）如图，在△ABC中，CD为角平分线，∠A＝40°，∠B＝60°，求证：CD为△ABC的“优美分割线”.
2. （2）在△ABC中，∠A＝46°，CD为△ABC的“优美分割线”且△ACD为等腰三角形，求∠ACB的度数.
3. （3）在△ABC中，∠A＝30°，AC＝6，CD为△ABC的“优美分割线”，且△ACD是等腰三角形，求线段BD的长.
答案解析收藏纠错 + 选题
25. (2022·广元模拟) 如图1，在平面直角坐标系xOy中，直线l：y＝ $\text{[math]}$ x+m与x轴、y轴分别交于点A和点B（0，﹣1），抛物线y＝ $\text{[math]}$ x²+bx+c经过点B，且与直线l的另一个交点为C（4，n）．
1. （1）求n的值和抛物线的解析式；
2. （2）点D在抛物线上，且点D的横坐标为t（0＜t＜4）．DE∥y轴交直线l于点E，点F在直线l上，且四边形DFEG为矩形（如图2），点H是直线BC上横坐标为﹣3的点．
  ①若矩形DFEG的周长为p，求p与t的函数关系式以及p的最大值；
  
  ②在p取最大值时，有一动点Q从点H出发，以每秒v个单位的速度沿射线HB运动到I点，然后以每秒 $\text{[math]}$ v个单位的速度从点I运动到点D，若要点Q所用时间最少直接写出点I的坐标；
3. （3）把直线BC绕着点A逆时针旋转45°，得到直线l′，点M是位于x轴上方的直线l′上的一动点，是否存在点M，使∠OMA＝∠ABO？若存在，请求出M点坐标：如果不存在，请说明理由．
答案解析收藏纠错 + 选题