北京市房山区2022年九年级中考数学一模考试

更新时间：2022-05-24 浏览次数：109 类型：中考模拟

一、单选题

1. (2022·房山模拟) 如图是某几何体的三视图，该几何体是（）

A . 三棱柱 B . 长方体 C . 圆锥 D . 圆柱

答案解析收藏纠错 + 选题
2. (2022·房山模拟) 2021年我国加大农村义务教育薄弱环节建设力度，提高学生营养改善计划补助标准，约37000000学生受益．将37000000用科学记数法表示应为（）

A . 0.37×10⁶ B . 3.7×10⁶ C . 3.7×10⁷ D . 37×10⁶

答案解析收藏纠错 + 选题
3. (2022·房山模拟) 实数a，b，c在数轴上的对应点的位置如图所示，下列结论中正确的是（）

A . b-c＜0 B . b＞-2 C . a+c＞0 D . |b|＞|c|

答案解析收藏纠错 + 选题
4. (2022·禄劝模拟) 下列多边形中，内角和为720°的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2022·房山模拟) 下列图形中，既是中心对称图形也是轴对称图形的是（）

A . 平行四边形 B . 等腰三角形 C . 正五边形 D . 矩形

答案解析收藏纠错 + 选题
6. (2022·房山模拟) 将宽为2 cm的长方形纸条折叠成如图所示的形状，那么折痕AB的长是（）

A . $\text{[math]}$ cm B . 2 $\text{[math]}$ cm C . 4cm D . $\text{[math]}$ cm

答案解析收藏纠错 + 选题
7. (2022·房山模拟) 第 24 届冬奥会将于 2022 年在北京和张家口举行，冬奥会的项目有滑雪（如跳台滑雪、高山滑雪、单板滑雪等）、滑冰（如短道速滑、速度滑冰、花样滑冰等）、冰球、冰壶等．如图，有 5 张形状、大小、质地均相同的卡片，正面分别印有高山滑雪、速度滑冰、冰球、单板滑雪、冰壶五种不同的图案，背面完全相同．现将这 5 张卡片洗匀后正面向下放在桌子上，从中随机抽取一张，抽出的卡片正面恰好是滑雪项目图案的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022·房山模拟) 某长方体木块的底面是正方形，它的高比底面边长还多50cm，把这个长方体表面涂满油漆时，如果每平方米费用为16元，那么总费用与底面边长满足的函数关系是（）

A . 正比例函数关系 B . 一次函数关系 C . 反比例函数关系 D . 二次函数关系

答案解析收藏纠错 + 选题

二、填空题

9. (2024八下·永寿期末) 若代数式 $\text{[math]}$ 有意义，则实数x的取值范围是.

答案解析收藏纠错 + 选题
10. (2022·房山模拟) 如图，在△ABC 中，AB＝AC，AB 的垂直平分线 MN 交 AC 于 D 点．若 BD 平分∠ABC，则∠A＝．

答案解析收藏纠错 + 选题
11. (2022·房山模拟) 已知关于x的一元二次方程 $\text{[math]}$ 有两个不相等的实数根，则a的取值范围是．

答案解析收藏纠错 + 选题
12. (2023·荷塘模拟) 写出一个比 $\text{[math]}$ 大且比4小的无理数．

答案解析收藏纠错 + 选题
13. (2022·房山模拟) 如图，点A，B，C在⊙O上，若∠OCB=20°，则∠A度数为．

答案解析收藏纠错 + 选题
14. (2022·房山模拟) 已知点A(1，2)，B在反比例函数 $\text{[math]}$ 的图象上，若OA=OB，则点B的坐标为．

答案解析收藏纠错 + 选题
15. (2022·房山模拟) 下表记录了甲、乙、丙三名射击运动员最近几次选拔赛成绩的平均数和方差：

甲
乙
丙
平均数
9.35
9.35
9.34
方差
6.6
6.9
6.7
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择．

答案解析收藏纠错 + 选题
16. (2022·房山模拟) 某市为进一步加快文明城市的建设，园林局尝试种植A、B两种树种．经过试种后发现，种植A种树苗a棵，种下后成活了 $\text{[math]}$ 棵，种植B种树苗b棵，种下后成活了（b-2）棵．第一阶段两种树苗共种植40棵，且两种树苗的成活棵树相同，则种植A种树苗棵．第二阶段，该园林局又种植A种树苗m棵，B种树苗n棵，若m=2n，在第一阶段的基础上进行统计，则这两个阶段种植A种树苗成活棵数种植B种树苗成活棵数（填“＞”“＜”或“＝”）．

答案解析收藏纠错 + 选题

三、解答题

17. (2022·房山模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2022·房山模拟) 解不等式组： $\text{[math]}$

答案解析收藏纠错 + 选题
19. (2024九下·北京市模拟) 已知 $\text{[math]}$ ，求代数式 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
20. (2022·房山模拟) 已知：如图，点M为锐角∠APB 的边PA上一点．
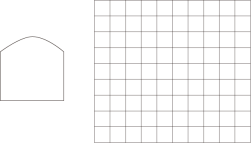
求作：∠AMD，使得点D在边PB上，且∠AMD ＝2∠P．
作法：
①以点M为圆心，MP长为半径画圆，交PA于另一点C，交PB于点D点；
②作射线MD．
1. （1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
2. （2）完成下面的证明．
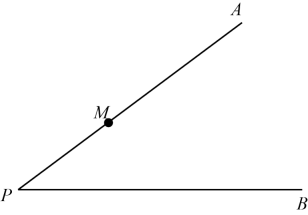
  证明：∵P、C、D都在⊙M 上，
  ∠P为弧CD所对的圆周角，∠CMD为弧CD所对的圆心角，
  ∴∠P＝ $\text{[math]}$ ∠CMD（）（填推理依据）．
  ∴∠AMD＝2∠P．
答案解析收藏纠错 + 选题
21. (2022·房山模拟) 如图，一个单向隧道的断面，隧道顶是一条抛物线的一部分，经测量，隧道顶的跨度为4米，最高处到地面的距离为4米，两侧墙高均为3米，距左侧墙壁1米和3米时，隧道高度均为3.75米．设距左侧墙壁水平距离为x米的地点，隧道高度为y米．
请解决以下问题：
1. （1）在网格中建立适当的平面直角坐标系，根据题中数据描点，并用平滑的曲线连接；
2. （2）请结合所画图象，写出抛物线的对称轴；
3. （3）今有宽为2.4米的卡车在隧道中间行驶，如果卡车载物后的高度为3.2米，要求卡车从隧道中间通过时，为保证安全，要求卡车载物后最高点到隧道顶面对应的点的距离均不小于0.6米，结合所画图象，试判断该卡车能否通过隧道．
答案解析收藏纠错 + 选题
22. (2022·房山模拟) 如图，在平行四边形ABCD中，过点B作BE⊥CD交CD的延长线于点E，过点C作CF $\text{[math]}$ EB交AB的延长线于点F．
1. （1）求证：四边形BFCE是矩形；
2. （2）连接AC，若AB=BE=2， $\text{[math]}$ ，求AC的长
答案解析收藏纠错 + 选题
23. (2022·房山模拟) 如图1，一次函数y=kx+4k（k≠0）的图象与x轴交于点A，与y轴交于点B，且经过点C（2，m）．
1. （1）当 $\text{[math]}$ 时，求一次函数的解析式并求出点A的坐标；
2. （2）当x>-1时，对于x的每一个值，函数y=x的值大于一次函数y=kx+4k（k≠0）的值，求k的取值范围．
答案解析收藏纠错 + 选题
24. (2022·房山模拟) 如图，BE是⊙O直径，点A是⊙O外一点：OA⊥OB，AP切⊙O于点P，连接BP交AO于点C．
1. （1）求证：∠PAO=2∠PBO；
2. （2）若⊙O的半径为5， $\text{[math]}$ ，求BP的长．
答案解析收藏纠错 + 选题
25. (2022·房山模拟) 为庆祝中国共产党建党100周年，讴歌中华民族实现伟大复兴的奋斗历程，继承革命先烈的优良传统，某中学开展了建党100周年知识测试．该校七、八年级各有300名学生参加，从中各随机抽取了50名学生的成绩（百分制），并对数据（成绩）进行整理，描述和分析，下面给出了部分信息：
a．八年级的频数分布直方图如下（数据分为5组：50≤x<60﹐60≤x<70，70≤x<80，80≤x<90，90≤x≤100）；
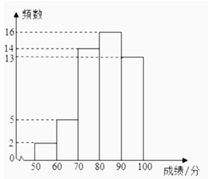
b．八年级学生成绩在80≤x<90的这一组是：
80 81 82 83 83 83.5 83.5 84 84 85 86 86.5 87 88 89 89
c．七、八年级学生成绩的平均数、中位数、众数如下：
年级
平均数
中位数
众数
七年级
87.2
85
91
八年级
85.3
m
90
根据以上信息，回答下列问题：
1. （1）表中m的值为；
2. （2）在随机抽样的学生中，建党知识成绩为84分的学生，在年级抽样学生中排名更靠前，理由是；
3. （3）若成绩85分及以上为“优秀”，请估计八年级达到“优秀”的人数．
答案解析收藏纠错 + 选题
26. (2022·房山模拟) 已知二次函数y=x²+bx+c（b，c为常数）的图象经过点A（1，0）与点C（0，-3），其顶点为P．
1. （1）求二次函数的解析式及P点坐标；
2. （2）当m≤x≤m+1时，y的取值范围是-4≤y≤2m，求m的值．
答案解析收藏纠错 + 选题
27. (2022·房山模拟) 已知：等边△ABC，过点B作AC的平行线l．点P为射线AB上一个动点（不与点A，B重合），将射线PC绕点P顺时针旋转60°交直线l于点D．
1. （1）如图1，点P在线段AB上时，依题意补全图形；
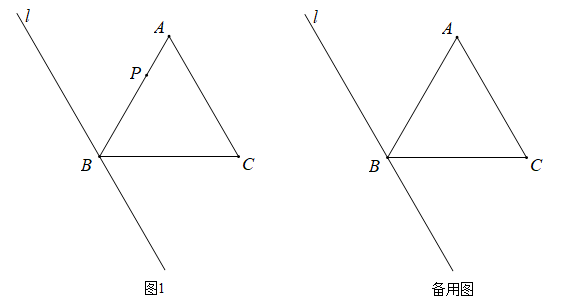
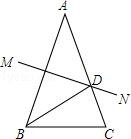
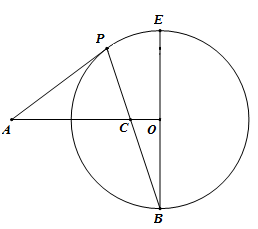
  ①求证：∠BDP=∠PCB；
  ②用等式表示线段BC，BD，BP之间的数里关系，并证明；
2. （2）点P在线段AB的延长线上，直接写出线段BC，BD，BP之间的数量关系．
答案解析收藏纠错 + 选题
28. (2022·房山模拟) 如图1，⊙I与直线a相离，过圆心I作直线a的垂线，垂足为H，且交⊙I于P，Q两点（Q在P，H之间）．我们把点P称为⊙I关于直线a的“远点”，把PQ·PH的值称为⊙I关于直线a的“特征数”．
1. （1）如图2，在平面直角坐标系xOy中，点E的坐标为（0，4），半径为1的⊙O与两坐标轴交于点A，B，C，D．
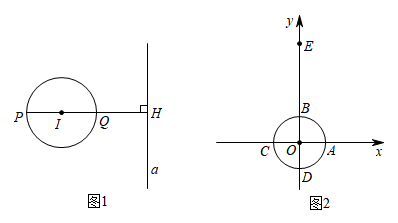
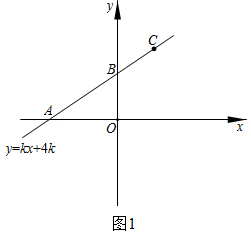
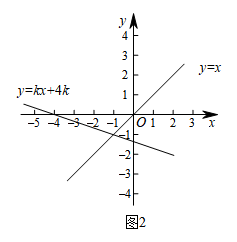
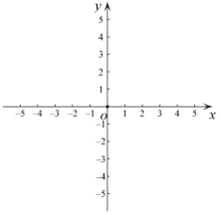
  ①过点E作垂直于y轴的直线m﹐则⊙O关于直线m的“远点”是点 ▲ （填“A”，“B”，“C”或“D”），⊙O关于直线m的“特征数”为 ▲ ；
  ②若直线n的函数表达式为 $\text{[math]}$ ，求⊙O关于直线n的“特征数”；
2. （2）在平面直角坐标系xOy、中，直线l经过点M（1，4），点F是坐标平面内一点，以F为圆心， $\text{[math]}$ 为半径作⊙F．若⊙F与直线l相离，点N（–1，0）是⊙F关于直线l的“远点”，且⊙F关于直线l的“特征数”是 $\text{[math]}$ ，直接写出直线l的函数解析式．
答案解析收藏纠错 + 选题