甘肃省酒泉市肃州区2022年中考适应性检测（一）数学试题

更新时间：2022-07-21 浏览次数：111 类型：中考模拟

一、单选题

1. (2023七下·义乌开学考) -2022的相反数是（）

A . 2022 B . -2022 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·肃州模拟) 冬季奥林匹克运动会是世界规模最大的冬季综合性运动会，每四年举办一次，第24届冬奥会将于2022年在北京和张家口举办.下列四个图分别是第24届冬奥会图标中的一部分，其中是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023七下·槐荫期中) 芝麻被称为“八谷之冠”，是世界上最古老的油料作物之一，它作为食物和药物，得到广泛的使用．经测算，一粒芝麻的质量约为0.00000201kg，将0.00000201用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022·肃州模拟) 下列计算结果为 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022·肃州模拟) 甲，乙，丙，丁四位男同学的5次足球30米S型绕杆运球的平均时间x（秒）及方差 $\text{[math]}$ 如下表所示，则这四名同学成绩最好的是（）

甲
乙
丙
丁
x
9.5
9.5
10
10
$\text{[math]}$
0.2
0.45
0.2
0.45

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
6. (2022·肃州模拟) 将一个含有30°角的直角三角板和一把直尺按如图方式放置，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . 120° B . 125° C . 130° D . 135°

答案解析收藏纠错 + 选题
7. (2022·肃州模拟) 如图，有座塔在河流北岸的点E处，一棵树位于河流南岸的点A处，从点A处开始，在河流南岸立4根标杆，以这4根标杆为顶点，组成边长为10米的正方形ABCD，且A，D，E三点在一条直线上，在标杆B处观察塔E，视线BE与边DC相交于点F，如果测得 $\text{[math]}$ 米，那么塔与树的距离AE为（）

A . 15米 B . 20米 C . 25米 D . 30米

答案解析收藏纠错 + 选题
8. (2024七下·任丘期中) 为了能让更多人接种，某药厂的新冠疫苗生产线开足马力，24小时运转，该条生产线计划加工320万支疫苗，前5天按原计划的速度生产，5天后以原来速度的1.25倍生产，结果比原计划提前3天完成任务．设原计划每天生产 $\text{[math]}$ 万支疫苗，则可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022·肃州模拟) 如图，AB是 $\text{[math]}$ 的直径，CD是 $\text{[math]}$ 的弦，连接BD、BC，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . 34° B . 56° C . 68° D . 102°

答案解析收藏纠错 + 选题
10. (2022·肃州模拟) 如图1，点P从 $\text{[math]}$ 的顶点A出发，沿 $\text{[math]}$ 匀速运动到点C，图2是点P运动时线段 $\text{[math]}$ 的长度y随时间x变化的关系图象，其中点Q为曲线部分的最低点，则 $\text{[math]}$ 的边 $\text{[math]}$ 的长度为（）

A . 12 B . 8 C . 10 D . 13

答案解析收藏纠错 + 选题

二、填空题

11. (2022·肃州模拟) 因式分解 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2022九上·南宁月考) 在数学实践课上，同学们进行投针试验：在平面上有一组平行线，相邻两条平行线间的距离都为5cm，将一根长度为3cm的针任意投掷在这个平面上，针可能与某一直线相交，也可能与任一直线都不相交，下表记录了他们的试验数据．
试验次数n
50
100
200
500
1000
2000
相交频数m
23
48
83
207
404
802
相交频率 $\text{[math]}$
0.460
0.480
0.415
0.414
0.404
0.401
若进行一次投针试验，估计针与直线相交的概率是（结果保留小数点后一位）．

答案解析收藏纠错 + 选题
13. (2024八下·宿城期末) 要使分式 $\text{[math]}$ 有意义，则x的取值范围为．

答案解析收藏纠错 + 选题
14. (2022八下·济南期末) 若关于x的一元二次方程 $\text{[math]}$ 有实数根，则k的取值范围是．

答案解析收藏纠错 + 选题
15. (2022·肃州模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， AD平分 $\text{[math]}$ 交BC于点D，点E、F分别是AD、AC的中点，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
16. (2022八上·余姚竞赛) 定义：如果三角形的一个内角是另一个内角的2倍，那么称这个三角形为“倍角三角形”，若一个等腰三角形恰好是“倍角三角形”，则它的顶角度数为．

答案解析收藏纠错 + 选题
17. (2022·肃州模拟) 如图，在半圆O中， $\text{[math]}$ ，点C是 $\text{[math]}$ 的中点，则图中阴影部分的面积是．

答案解析收藏纠错 + 选题
18. (2022·肃州模拟) 按一定规律排列的多项式： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …，根据上述规律，则第n个多项式是．

答案解析收藏纠错 + 选题

三、解答题

19. (2022·肃州模拟) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2022·肃州模拟) 化简求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2022·肃州模拟) 如图，已知点D在△ABC的边AB上，且AD＝CD，
1. （1）用直尺和圆规作∠BDC的平分线DE，交BC于点E（不写作法，保留作图痕迹）；
2. （2）在（1）的条件下，判断DE与AC的位置关系，并写出证明过程．
答案解析收藏纠错 + 选题
22. (2022·肃州模拟) 敦煌莫高窟是中国现存规模最大、保存最为完好的佛教艺术宝库，被誉为“沙漠中的古代艺术画廊”，位于石窟群中段的红色楼阁（如图①），便是莫高窟标志性建筑——九层楼．某数学兴趣小组想利用所学的知识测量莫高窟九层楼的高度，并画出示意图如图②所示．具体方法如下：在地面C处测得楼顶A的仰角为60°，此时无人机从地面C处垂直上升到点D处，测得楼顶A的仰角为53.5°，且 $\text{[math]}$ ．已知点A，B，C，D在同一平面内，求莫高窟九层楼的高度AB．（结果保留整数，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
23. (2024九上·随县月考) 邮票素有“国家名片”之称，方寸之间，包罗万象．为宣传北京2022年冬奥会，中国邮政发行了若干套冬奥会纪念邮票，其中有一套展现雪上运动的邮票，如图所示：
某班级举行冬奥会有奖问答活动，答对的同学可以随机抽取邮票作为奖品．
1. （1）在抢答环节中，若答对一题，可从4枚邮票中任意抽取1枚作为奖品，则恰好抽到“冬季两项”的概率是．
2. （2）在抢答环节中，若答对两题，可从4枚邮票中任意抽取2枚作为奖品，请用列表或画树状图的方法，求恰好抽到“高山滑雪”和“自由式滑雪”的概率．
答案解析收藏纠错 + 选题
24. (2022·肃州模拟) 世界卫生组织预计：到2025年，全世界将会有一半人面临用水危机.为了倡导“节约用水，从我做起”，某县政府决定对县直属机关500户家庭一年的月平均用水量进行调查，调查小组随机抽查了部分家庭的月平均用水量（单位：吨），并将调查结果绘制成如图所示的条形统计图和扇形统计图.

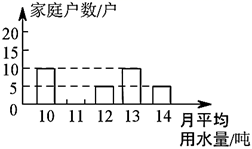
根据以上提供的信息，解答下列问题：
1. （1）将条形统计图补充完整；
2. （2）求被调查家庭的月平均用水量的中位数吨、众数吨；
3. （3）估计该县直属机关 $\text{[math]}$ 户家庭的月平均用水量不少于 $\text{[math]}$ 吨的约有多少户？
答案解析收藏纠错 + 选题
25. (2022·肃州模拟) 心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y随时间x（分）的变化规律如图12所示（其中AB，BC分别为线段，CD为双曲线的一部分）：
1. （1）开始上课后第5分钟与第30分钟相比较，何时学生的注意力更集中？
2. （2）一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题？
答案解析收藏纠错 + 选题
26. (2024·砚山模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径，点C是 $\text{[math]}$ 上异于A、B的点，连接 $\text{[math]}$ 、 $\text{[math]}$ ，点D在 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ ，点E在 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线：
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
27. (2021九上·抚远期中) 已知：正方形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 绕点A顺时针旋转，它的两边分别交 $\text{[math]}$ （或它们的延长线）于点 $\text{[math]}$ ．
当 $\text{[math]}$ 绕点A旋转到 $\text{[math]}$ 时（如图1），易证 $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ 绕点A旋转到 $\text{[math]}$ 时（如图2），线段 $\text{[math]}$ 和 $\text{[math]}$ 之间有怎样的数量关系？写出猜想，并加以证明．
2. （2）当 $\text{[math]}$ 绕点A旋转到如图3的位置时，线段 $\text{[math]}$ 和 $\text{[math]}$ 之间又有怎样的数量关系？请直接写出你的猜想．
答案解析收藏纠错 + 选题
28. (2022·肃州模拟) 如图，抛物线y＝ax²＋bx＋c与坐标轴交于点A（0，﹣3）、B（﹣1，0）、E（3，0），点P为抛物线上动点，设点P的横坐标为t．
1. （1）若点C与点A关于抛物线的对称轴对称，求C点的坐标及抛物线的解析式；
2. （2）若点P在第四象限，连接PA、PE及AE，当t为何值时，△PAE的面积最大？最大面积是多少？
3. （3）是否存在点P，使△PAE为以AE为直角边的直角三角形，若存在，直接写出点P的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题