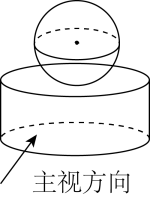
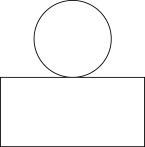
 B .
B .  C .
C . 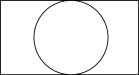 D .
D . 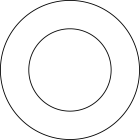
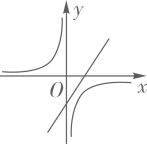 B .
B .  C .
C .  D .
D . 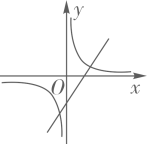
|
睡眠时间 |
频数 |
频率 |
|
|
3 |
0.06 |
|
|
|
0.16 |
|
|
10 |
0.20 |
|
|
24 |
|
|
|
5 |
0.10 |
请根据统计表中的信息回答下列问题.