人教版七上数学第四章4.3.2角的比较与运算课时易错题三刷...

更新时间：2022-10-08 浏览次数：122 类型：同步测试

一、单选题

1. (2021七上·陇县期末) 如图，OB是∠AOC的平分线，∠COD＝ $\text{[math]}$ ∠BOD，∠COD＝17°，则∠AOD的度数是（）

A . 70° B . 83° C . 68° D . 85°

答案解析收藏纠错 + 选题
2. (2022七下·东昌府月考) 如图，∠AOB，以OA为边作∠AOC，使∠BOC= $\text{[math]}$ ∠AOB，则下列结论成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

3. (2021七上·番禺期末) 如图，若∠AOB＝90°，∠COD＝90°，∠AOD＝20°，则∠BOC的大小为 °．

答案解析收藏纠错 + 选题
4. (2021七上·利通期末) 如图，已知OD平分∠AOC，OE平分∠COB，∠AOD＝20°，∠EOB＝40°.则∠AOB＝.

答案解析收藏纠错 + 选题
5. (2022七下·仁怀月考) 如图，将一个三角板60°角的顶点与另一个三角板的直角顶点重合，∠1＝27°41′，∠2的大小是 .

答案解析收藏纠错 + 选题
6. (2021七上·长沙期末) 如图，在∠AOB的内部有3条射线OC、OD、OE，若∠AOC＝70°，∠BOE＝ $\text{[math]}$ ∠BOC，∠BOD＝ $\text{[math]}$ ∠AOB，则∠DOE＝°.（用含n的代数式表示）

答案解析收藏纠错 + 选题

三、解答题

7. (2021七上·丰台期末) 补全解题过程．
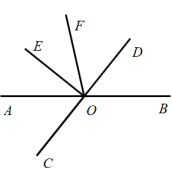
已知：如图，∠AOB＝40°，∠BOC＝70°，OD平分∠AOC．
求∠BOD的度数．
解：∵∠AOB＝40°，∠BOC＝70°，
∴∠AOC＝∠AOB＋∠BOC＝                   ▲                  °．
∵OD平分∠AOC，
∴∠AOD＝ $\text{[math]}$ ∠                  ▲                  （                  ▲                  ）（填写推理依据）．
∴∠AOD＝                  ▲                  °．
∴∠BOD＝∠AOD﹣∠                  ▲                   ．
∴∠BOD＝                  ▲                  °．

答案解析收藏纠错 + 选题
8. (2021七上·怀柔期末) 完成下列说理过程（括号中填写推理的依据）：
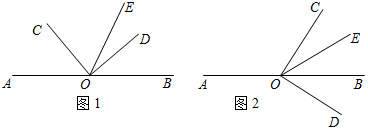
已知：如图，直线AB，CD相交于点O， $\text{[math]}$ ．求证： $\text{[math]}$ ．
证明： $\text{[math]}$ ，
$\text{[math]}$ ．（                  ▲                  ）
$\text{[math]}$ ，
$\text{[math]}$ ．
$\text{[math]}$ 直线AB，CD相交于点O，
$\text{[math]}$ ．
$\text{[math]}$ $\text{[math]}$ ．
$\text{[math]}$ $\text{[math]}$ ＝                  ▲                   ．（                  ▲                  ）
$\text{[math]}$ 直线 $\text{[math]}$ 相交于 $\text{[math]}$ ，
$\text{[math]}$ ．
$\text{[math]}$                   ▲                   ．（                  ▲                  ）
$\text{[math]}$ ．

答案解析收藏纠错 + 选题
9. (2021七上·永定期末) 如图，已知 $\text{[math]}$ 平分 $\text{[math]}$ ，∠COD=20°，求 $\text{[math]}$ 的度数.

答案解析收藏纠错 + 选题

四、综合题

10. (2021七上·密山期末) 如图，点O是直线AB上的一点，∠COD是直角，OE平分∠BOC．
1. （1）如图（1），若∠AOC=40°，求∠DOE的度数；
2. （2）如图（2），若∠COE=∠DOB，求∠AOC的度数．
答案解析收藏纠错 + 选题
11. (2021七上·河南期末) 如图1，将一副三角尺的直角顶点O叠放在一起.若三角尺AOB不动，将三角尺COD绕点O按顺时针方向转动α（0°<α<180°）.
1. （1）如图2，若∠BOC=55°，则∠AOD=，∠AOC∠BOD（填“>”、“<”或“=”）；
2. （2）如图3，∠BOC=55°，则∠AOD=，∠AOC∠BOD（填“>”、“<”或“=”）.
3. （3）三角尺COD在转动的过程中，若∠BOC=β，则∠AOD=（用含β的代数式表示），∠AOC∠BOD（填“>”、“<”或“=”）.
4. （4）借助（3）中的结论，在备用图中利用画直角的工具画出一个与∠AOC相等的角.
答案解析收藏纠错 + 选题
12. (2021七上·密云期末) 已知：∠AOB=120°，∠COD=90°，OE平分∠AOD．
1. （1）如图1，当∠COD的边OD在∠AOB内部时，若∠COE=40°，求∠BOD的度数；
2. （2）如图2，当∠COD的边OD在∠AOB外部，且0°<∠BOD<60°时，设∠COE=α，∠BOD=β，用等式表示α与β之间的数量关系，并证明．
答案解析收藏纠错 + 选题
13. (2022七上·渠县期末) 阅读下面材料：
数学课上，老师给出了如下问题：

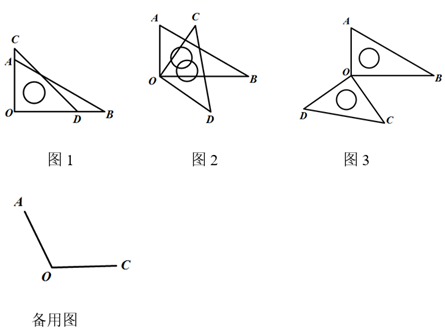
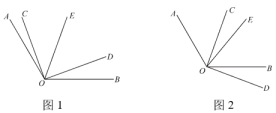
如图1，∠AOB＝80°，OC平分∠AOB，若∠BOD＝20°，请你补全图形，并求∠COD的度数.

以下是小明的解答过程：

解：如图2，因为OC平分∠AOB，∠AOB＝80°，

所以∠BOC＝_____∠AOB＝_____°

因为∠BOD＝20°，

所以∠COD＝______°

小静说：“我觉得这个题有两种情况，小明考虑的是OD在∠AOB外部的情况，事实上，OD还可能在∠AOB的内部”.

完成以下问题：
1. （1）请你将小明的解答过程补充完整；
2. （2）根据小静的想法，请你在图3中画出另一种情况对应的图形，并直接写出此时∠COD的度数为▲ °
答案解析收藏纠错 + 选题
14. (2021七上·香洲期末) 已知射线OB，OC在钝角 $\text{[math]}$ 的内部，且满足 $\text{[math]}$ ，射线OE，OF分别平分 $\text{[math]}$ ．
1. （1）如图1，当射线OC在射线OB的左侧时， $\text{[math]}$ ，
  ①若 $\text{[math]}$ ， $\text{[math]}$ ▲ ；
  ②若 $\text{[math]}$ ， $\text{[math]}$ ▲ ；
  ③若 $\text{[math]}$ ，计算 $\text{[math]}$ 的度数．
2. （2）当射线OC在射线OB的右侧时，设 $\text{[math]}$ ，请画出图形并计算 $\text{[math]}$ 的度数（用含 $\text{[math]}$ 的式子表示）．
答案解析收藏纠错 + 选题
15. (2022七上·毕节期末) 如图，点O为直线AB上一点， $\text{[math]}$ ，OD平分 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的度数：
2. （2）作射线OE，使 $\text{[math]}$ ，求 $\text{[math]}$ 的度数.
答案解析收藏纠错 + 选题
16. (2021七上·安吉期末) 已知∠AOB＝160°，∠COE是直角，OF平分∠AOE.
1. （1）如图1，若∠COF＝32°，则∠BOE＝；
2. （2）如图1，若∠COF＝m°，则∠BOE＝；∠BOE与∠COF的数量关系为；
3. （3）在已知条件不变的前提下，当∠COE绕点O逆时针转动到如图2的位置时，第（2）问中∠BOE与∠COF的数量关系是否仍然成立？请说明理由.
答案解析收藏纠错 + 选题