北京市丰台区2021-2022学年八年级下学期期末数学试题

更新时间：2024-07-13 浏览次数：107 类型：期末考试

一、单选题

1. (2024九下·孝感模拟) 函数y＝ $\text{[math]}$ 中自变量x的取值范围是（）

A . x＞3 B . x≥3 C . x≠3 D . x＜3

答案解析收藏纠错 + 选题
2. (2024八下·民勤期末) 一家鞋店在某种运动鞋进货的过程中，商家关注的是卖出的这种运动鞋尺码组成的一组数据的（）

A . 平均数 B . 中位数 C . 众数 D . 方差

答案解析收藏纠错 + 选题
3. (2022八下·丰台期末) 下列各曲线中，不能表示 $\text{[math]}$ 是x的函数的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023八下·赫山期末) 下面的多边形中，内角和与外角和相等的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2024八下·临沂月考) 在 $\text{[math]}$ 中，∠A，∠B，∠C的对边分别是a，b，c，下列条件中，不能判定 $\text{[math]}$ 是直角三角形的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024八下·北京市期中) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022八下·丰台期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点D是边AC的中点，点E是边AB的中点，则 $\text{[math]}$ 的周长是（）

A . 6 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022八下·丰台期末) 匀速地向一个容器内注水，最后把容器注满．在注水过程中，水面高度h随时间t的变化规律如图所示（图中 $\text{[math]}$ 是一条折线）．这个容器的形状可能是下面图中的（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

9. (2024八下·南宁月考) 计算： $\text{[math]}$ = ．

答案解析收藏纠错 + 选题
10. (2022八下·丰台期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，则∠C的度数是．

答案解析收藏纠错 + 选题
11. (2024九上·北京市开学考) 如果一次函数 $\text{[math]}$ 的图象经过 $\text{[math]}$ ，且y随x的增大而增大，那么这个一次函数的解析式可以是（写出一个即可）．

答案解析收藏纠错 + 选题
12. (2023八下·东城期中) 每年的4月23日是“世界读书日”，某校为了解4月份八年级学生的读书情况，随机调查了八年级50名学生读书的册数，数据整理如下：
册数
0
1
2
3
4
人数
9
3
20
15
3
由此估计该校八年级学生4月份人均读书册．

答案解析收藏纠错 + 选题
13. (2022八下·丰台期末) 如图，在四边形ABCD中，对角线AC，BD相交于点O，E，F，G，H分别是边AB，BC，CD，DA的中点，只需添加一个条件，即可证明四边形EFCH是矩形，这个条件可以是（写出一个即可）．

答案解析收藏纠错 + 选题
14. (2022八下·丰台期末) 农科院为某地选择甲、乙两种甜玉米种子时，甜玉米的产量和产量的稳定性是农科院所关心的问题，他们各用10块自然条件相同的试验田进行试验，下图是试验后得到的各试验田两种种子每公顷的产量（单位：t）．已知甲、乙两种甜玉米种子的平均产量相差不大，那么由样本估计总体，推测这个地区比较适合种植（填“甲”或“乙”）种甜玉米，理由是．

答案解析收藏纠错 + 选题
15. (2022八下·丰台期末) 如图1，四个全等的直角三角形围成一个大正方形，中间是一个小正方形，这个图形是我国汉代赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”．连接四条线段得到如图2的新的图案．如果图1中的直角三角形的长直角边为5，短直角边为3，图2中阴影部分的面积为S，那么S的值为．

答案解析收藏纠错 + 选题
16. (2022八下·丰台期末) 在等边 $\text{[math]}$ 中，AD为边BC的中线，将此三角形沿AD剪开成两个三角形，然后把这两个三角形拼成一个平行四边形，如果 $\text{[math]}$ ，那么在所有能拼成的平行四边形中，对角线长度的最大值是．

答案解析收藏纠错 + 选题

三、解答题

17. (2022八下·丰台期末) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2022八下·丰台期末) 已知 $\text{[math]}$ ，求代数式 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
19. (2022八下·丰台期末) 已知： $\text{[math]}$ ．
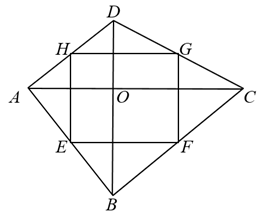
求作：直线AD，使得 $\text{[math]}$ ．
作法：如图，
①分别以点A、点C为圆心，大于 $\text{[math]}$ 长为半径画弧，两弧相交于点M、点N；
②作直线MN交AC于点E；
③以点E为圆心，BE长为半径画弧，交射线BE于点D；
④作直线AD．
所以直线AD就是所求作的直线．
1. （1）使用直尺和圆规，补全图形；（保留作图痕迹）
2. （2）完成下面的证明．
  证明：连接CD，
  ∵ $\text{[math]}$       ▲ ， $\text{[math]}$       ▲ ，
  ∴四边形ABCD是平行四边形，（      ）（填推理的依据）．
  ∴ $\text{[math]}$ （     ）（填推理的依据）．
答案解析收藏纠错 + 选题
20. (2022八下·丰台期末) 在平面直角坐标系xOy中，一次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ．
1. （1）求k的值；
2. （2）画出一次函数的图象；
3. （3）根据图象回答：当自变量x的取值范围是时，函数值 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2024九下·昆明开学考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， DE平分∠BDC交BC于点O，交AB的延长线于点E，连接CE．
1. （1）求证：四边形BECD是菱形；
2. （2）如果 $\text{[math]}$ ， $\text{[math]}$ ，求四边形BECD的面积．
答案解析收藏纠错 + 选题
22. (2022八下·丰台期末) 2021年12月《北京市义务教育体育与健康考核评价方案》正式发布，跳绳成为新增的体育中考选考项目．某校体育组为了解八年级学生跳绳的基本情况，从八年级男、女生中各随机抽取了20名学生1分钟跳绳次数，并对数据进行整理、描述和分析．下面给出了部分信息．
a．学生1分钟跳绳次数频数分布直方图如下（数据分成9组： $\text{[math]}$ ， $\text{[math]}$ ， …， $\text{[math]}$ ）：
b．男生1分钟跳绳次数在 $\text{[math]}$ 这一组的是：140，141，142，143，144，145，145，147
c.1分钟跳绳次数的平均数、中位数、优秀率如下表：
组别
平均数
中位数
优秀率
男生
139
m
65%
女生
135
138
n
注：《国家中学生体质健康标准》规定：八年级男生1分钟跳绳次数大于或等于135个，成绩为优秀；八年级女生1分钟跳绳次数大于或等于130个，成绩为优秀．
根据以上信息，回答下列问题：
1. （1）将女生1分钟跳绳次数频数分布直方图补充完整；
2. （2）写出表中m，n的值；
3. （3）此次测试中，某学生的1分钟跳绳次数为140个，这名学生的成绩排名超过同组一半的学生，判断该生属于（填“男生”或“女生”）组；
4. （4）如果全年级男生人数为100人，女生人数为120人，请估计该年级跳绳成绩优秀的总人数．
答案解析收藏纠错 + 选题
23. (2022八下·丰台期末) 在“一次函数”的课题学习中，某小组从购物节期间甲、乙两家商场的促销信息中发现并提出问题，请将他们分析、解决问题的过程补充完整．
甲商场：所有商品打8折；
乙商场：一次性购物不超过300元不打折，超过300元时，超出的部分打6折．
问题：在购买原价相同的同种商品时，应该如何选择这两家商场购物更省钱？
分析问题：
1. （1）设原价为x元，则甲、乙两家商场的购物金额分别y_甲元、y_乙元，得到相应的函数解析式：
  $\text{[math]}$ ， $\text{[math]}$ ，
  $\text{[math]}$ ；
2. （2）按照下表中自变量x的值代入解析式计算，分别得到了y_甲， y_乙的几组对应值；
  x/元
  0
  300
  600
  …
  y_甲/元
  0
  a
  480
  …
  y_乙/元
  0
  300
  b
  …
3. （3）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点，并画出函数y_甲， y_乙的图象；
  解决问题：
  根据以上分析，在购买原价相同的同种商品时，选择购物更省钱的方案是 ▲ ．
答案解析收藏纠错 + 选题
24. (2022八下·丰台期末) 在平面直角坐标系xOy中，一次函数 $\text{[math]}$ 的图象由正比例函数 $\text{[math]}$ 的图象向上平移2个单位长度得到．
1. （1）求这个一次函数的解析式；
2. （2）当 $\text{[math]}$ 时，对于x的每一个值，正比例函数 $\text{[math]}$ 的值小于一次函数 $\text{[math]}$ 的值，直接写出a的取值范围．
答案解析收藏纠错 + 选题
25. (2022八下·丰台期末) 如图，在正方形ABCD中，点E是直线AC上任意一点（不与点A，C重合），过点E作 $\text{[math]}$ 交直线CD于点F，过点F作 $\text{[math]}$ 交直线AC于点G．
1. （1）如图1，当点E在线段AC上时，猜想EG与AB的数量关系；
2. （2）如图2，当点E在线段AC的延长线上时，补全图形，并判断（1）中EG与AB的数量关系是否仍然成立．如果成立，请证明；如果不成立，请说明理由．
答案解析收藏纠错 + 选题
26. (2022八下·丰台期末) 在平面直角坐标系xOy中，对于点P与图形W给出如下定义：如果存在以点P为端点的一条射线与图形W有且只有2个公共点，那么称点P是图形W的“相关点”．已知点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ 时，
  ①在点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中，是折线 $\text{[math]}$ 的“相关点”的是▲ ；
  ②点M是直线 $\text{[math]}$ 上一点，如果点M是折线 $\text{[math]}$ 的“相关点”，求点M的横坐标 $\text{[math]}$ 的取值范围；
2. （2）正方形DEFG的各边都平行于坐标轴，对角线的交点N的坐标是 $\text{[math]}$ ．如果正方形的边长是2，正方形DEFG上的任意一点都是折线 $\text{[math]}$ 的“相关点”，请直接写出m的取值范围．
答案解析收藏纠错 + 选题