2022年秋季湘教版数学九年级上册第五章《用样本推断总体》...

更新时间：2022-10-23 浏览次数：133 类型：单元试卷

一、单选题（每题3分，共30分）

1. (2022·台湾) 某国主计处调查2017年该国所有受雇员工的年薪资料，并公布调查结果如图的直方图所示.

已知总调查人数为750万人，根据图中信息计算，该国受雇员工年薪低于平均数的人数占总调查人数的百分率为下列何者？（）

A . 6% B . 50% C . 68% D . 73%

答案解析收藏纠错 + 选题
2. (2022·乐山) 李老师参加本校青年数学教师优质课比赛，笔试得90分、微型课得92分、教学反思得88分.按照图所显示的笔试、微型课、教学反思的权重，李老师的综合成绩为（）

A . 88 B . 90 C . 91 D . 92

答案解析收藏纠错 + 选题
3. (2024九下·阳春模拟) 一组数据4、5、6、a、b的平均数为5，则a、b的平均数为（）

A . 4 B . 5 C . 8 D . 10

答案解析收藏纠错 + 选题
4. (2022九下·望花月考) 袁隆平院士被誉为“世界杂交水稻之父”，他研究的水稻，不仅高产，而且抗倒伏．在某次实验中，他的团队对甲、乙两种水稻品种进行产量稳定实验，各选取了8块条件相同的试验田，同时播种并核定亩产，结果甲、乙两种水稻的平均产量均为1200千克/亩，方差为 $\text{[math]}$ ， $\text{[math]}$ ．为保证产量稳定，适合推广的品种为（）

A . 甲 B . 乙 C . 甲、乙均可 D . 无法确定

答案解析收藏纠错 + 选题

5. (2024九下·南山模拟) 某校为推荐一项作品参加“科技创新”比赛，对甲、乙、丙、丁四项候选作品进行量化评分，具体成绩（百分制）如表：

项目

作品

甲

乙

丙

丁

创新性

实用性

如果按照创新性占60%，实用性占40%计算总成绩，并根据总成绩择优推荐，那么应推荐的作品是（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题

6. (2022·遵义) 2021年7月，中共中央办公厅、国务院办公厅印发《关于进一步减轻义务教有阶段学生作业负担和校外培训负担的意见》，明确要求初中生每天的书面作业时间不得超过90分钟.某校随机抽取部分学生进行问卷调查，并将调查结果制成如下不完整的统计图表.则下列说法不正确的是（）

作业时间频数分布

组别	作业时间（单位：分钟）	频数
$\text{[math]}$	$\text{[math]}$	8
$\text{[math]}$	$\text{[math]}$	17
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	5

作业时间扇形统计图

A . 调查的样本容量是为50 B . 频数分布表中m的值为20 C . 若该校有1000名学生，作业完成的时间超过90分钟的约100人 D . 在扇形统计图中B组所对的圆心角是144°

答案解析收藏纠错 + 选题

7. (2024七下·醴陵期末) 数据1，2，3，4，5，x存在唯一众数，且该组数据的平均数等于众数，则x的值为（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
8. (2022·广元) 如图是根据南街米粉店今年6月1日至5日每天的用水量（单位：吨）绘制成的折线统计图.下列结论正确的是（）

A . 平均数是6 B . 众数是7 C . 中位数是11 D . 方差是8

答案解析收藏纠错 + 选题
9. (2022·嘉兴) A，B两名射击运动员进行了相同次数的射击，下列关于他们射击成绩的平均数和方差的描述中，能说明A成绩较好且更稳定的是（）

A . $\text{[math]}$ ＞ $\text{[math]}$ 且 $\text{[math]}$ ＞ $\text{[math]}$ ． B . $\text{[math]}$ ＜ $\text{[math]}$ 且 $\text{[math]}$ ＞ $\text{[math]}$ ． C . $\text{[math]}$ ＞ $\text{[math]}$ 且 $\text{[math]}$ ＜ $\text{[math]}$ ． D . $\text{[math]}$ ＜ $\text{[math]}$ 且 $\text{[math]}$ ＜ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
10. (2024八下·长春期末) 一组数据：1，2，2，3，若添加一个数据3，则不发生变化的统计量是（）

A . 平均数 B . 中位数 C . 众数 D . 方差

答案解析收藏纠错 + 选题

二、填空题（每题3分，共18分）

11. (2021·宜宾) 从甲、乙、丙三人中选一人参加环保知识决赛，经过两轮测试，他们的平均成绩都是88.9，方差分别是 $\text{[math]}$ ，你认为最适合参加决赛的选手是（填“甲”或“乙”或“丙”）.

答案解析收藏纠错 + 选题
12. (2022·包头) 某校欲招聘一名教师，对甲、乙两名候选人进行了三项素质测试，各项测试成绩满分均为100分，根据最终成绩择优录用，他们的各项测试成绩如下表所示：
候选人
通识知识
专业知识
实践能力
甲
80
90
85
乙
80
85
90
根据实际需要，学校将通识知识、专业知识和实践能力三项测试得分按2：5：3的比例确定每人的最终成绩，此时被录用的是．（填“甲”或“乙”）

答案解析收藏纠错 + 选题

13. (2022·山西) 生物学研究表明，植物光合作用速率越高，单位时间内合成的有机物越多，为了解甲、乙两个品种大豆的光合作用速率，科研人员从甲、乙两个品种的大豆中各选五株，在同等实验条件下，测量它们的光合作用速率（单位： $\text{[math]}$ ），结果统计如下：

品种	第一株	第二株	第三株	第四株	第五株	平均数
甲	32	30	25	18	20	25
乙	28	25	26	24	22	25

则两个大豆品种中光合作用速率更稳定的是（填“甲”或“乙”）．

答案解析收藏纠错 + 选题

14. (2023八下·卧龙期末) 学校举行物理科技创新比赛，各项成绩均按百分制计，然后按照理论知识占20%，创新设计占50%，现场展示占30%计算选手的综合成绩（百分制），某同学本次比赛的各项成绩分别是：理论知识85分，创新设计88分，现场展示90分，那么该同学的综合成绩是分.

答案解析收藏纠错 + 选题
15. (2022·成武模拟) 已知甲、乙两队员射击的成绩如图，设甲、乙两队员射击成绩的方差分别为 $\text{[math]}$ 、 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ ．（填“ $\text{[math]}$ ”、“ $\text{[math]}$ ”、“ $\text{[math]}$ ”）

答案解析收藏纠错 + 选题
16. (2021·乐山) 如图是根据甲、乙两人5次射击的成绩（环数）制作的折线统计图.你认为谁的成绩较为稳？（填“甲”或“乙”）

答案解析收藏纠错 + 选题

三、解答题（共8题，共72分）

17. (2022·徐州) 如图，下列装在相同的透明密封盒内的古钱币，其密封盒上分别标有古钱币的尺寸及质量，例如：钱币“文星高照”密封盒上所标“ $\text{[math]}$ ”是指该枚古钱币的直径为 $\text{[math]}$ ，厚度为 $\text{[math]}$ ，质量为 $\text{[math]}$ ．已知这些古钱币的材质相同．
根据图中信息，解决下列问题．
1. （1）这5枚古钱币，所标直径的平均数是 $\text{[math]}$ ，所标厚度的众数是 $\text{[math]}$ ，所标质量的中位数是 g；
2. （2）由于古钱币无法从密封盒内取出，为判断密封盒上所标古钱币的质量是否有错，桐桐用电子秤测得每枚古钱币与其密封盒的总质量如下：
  名称
  文星高照
  状元及第
  鹿鹤同春
  顺风大吉
  连中三元
  总质量/g
  58.7
  58.1
  55.2
  54.3
  55.8
  请你应用所学的统计知识，判断哪枚古钱币所标的质量与实际质量差异较大，并计算该枚古钱币的实际质量约为多少克．
答案解析收藏纠错 + 选题

18. (2022·无锡) 育人中学初二年级共有200名学生，2021年秋学期学校组织初二年级学生参加30秒跳绳训练，开学初和学期末分别对初二年级全体学生进行了摸底测试和最终测试，两次测试数据如下：

育人中学初二学生30秒跳绳测试成绩的频数分布表

跳绳个数（x）	x≤50	50＜x≤60	60＜x≤70	70＜x≤80	x＞80
频数（摸底测试）	19	27	72	a	17
频数（最终测试）	3	6	59	b	c

育人中学初二学生30秒跳绳最终测试成绩的扇形统计图

（1）表格中a＝；
（2）请把下面的扇形统计图补充完整；（只需标注相应的数据）
（3）请问经过一个学期的训练，该校初二年级学生最终测试30秒跳绳超过80个的人数有多少？

答案解析收藏纠错 + 选题

19. (2023·百色模拟) 为了落实“双减”政策，提倡课内高效学习，课外时间归还学生，“鸿志”班为了激发学生学习热情，提高学习成绩，采用分组学习方案，每7人分为一小组，经过半个学期的学习，在模拟测试中，某小组7人的成绩分别为98，94，92，88，95，98，100（单位：分）.
1. （1）该小组学生成绩的中位数是，众数是.
2. （2）若成绩95分（含95分）以上评为优秀，求该小组成员成绩的平均分和优秀率（百分率保留整数）.
答案解析收藏纠错 + 选题

20. (2021·娄底) “读书，点亮未来”，广泛的课外阅读是同学们搜集和汲取知识的一条重要途径.学校图书馆计划购进一批学生喜欢的图书，为了了解学生们对“A文史类、B科普类、C生活类、D其它”的喜欢程度，随机抽取了部分学生进行问卷调查（每个学生只选其中一类），将所得数据进行分类统计绘制了如下不完整的统计图表，请根据图中的信息，解答下列问题：

统计表：

	频数	频率
A历史类	50	m
B科普类	90	0.45
C生活类	n	0.20
D其它	20	0.10
合计

（1）本次调查的学生共人；
（2） $\text{[math]}$ ， $\text{[math]}$ ；
（3）补全条形统计图.

答案解析收藏纠错 + 选题

21. (2022七下·大庆期末) 某校组织了一次“校徽设计”竞赛活动，邀请5名老师作为专业评委，50名学生代表参与民主测评，且民主测评的结果无弃权票.某作品的评比数据统计如下：
专业评委
给分（单位：分）
①
88
②
87
③
94
④
91
⑤
90
记“专业评委给分”的平均数为 $\text{[math]}$ .
1. （1）求该作品在民主测评中得到“不赞成”的票数；
2. （2）对于该作品，问 $\text{[math]}$ 的值是多少？
3. （3）记“民主测评得分”为 $\text{[math]}$ ， “综合得分”为 $\text{[math]}$ ，若规定：① $\text{[math]}$ “赞成”的票数 $\text{[math]}$ 分＋“不赞成”的票数 $\text{[math]}$ 分；② $\text{[math]}$ .求该作品的“综合得分” $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
22. (2021九上·新乐期末) 近5年，我省家电业的发展发生了新变化.以甲、乙、丙3种家电为例，将这3种家电2016～2020年的产量（单位：万台）绘制成如图所示的折线统计图，图中只标注了甲种家电产量的数据.

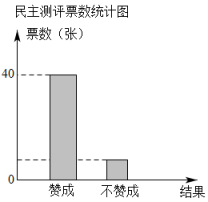
观察统计图回答下列问题：
1. （1）这5年甲种家电产量的中位数为万台；
2. （2）若将这5年家电产量按年份绘制成5个扇形统计图，每个统计图只反映该年这3种家电产量占比，其中有一个扇形统计图的某种家电产量占比对应的圆心角大于180°，这个扇形统计图对应的年份是年；
3. （3）小明认为：某种家电产量的方差越小，说明该家电发展趋势越好.你同意他的观点吗？请结合图中乙、丙两种家电产量变化情况说明理由.
答案解析收藏纠错 + 选题

23. (2021·北部湾) 某水果公司以10元/ $\text{[math]}$ 的成本价新进2000箱荔枝，每箱质量 $\text{[math]}$ ，在出售荔枝前，需要去掉损坏的荔枝，现随机抽取20箱，去掉损坏荔枝后称得每箱的质量（单位： $\text{[math]}$ ）如下：

4.7··4.8·4.6··4.5··4.8··4.9··4.8··4.7··4.8··4.7

4.8··4.9··4.7··4.8··4.5·4.7··4.7··4.9··4.7··5.0

整理数据：							分析数据：
质量（ $\text{[math]}$ ）	4.5	4.6	4.7	4.8	4.9	5.0	平均数	众数	中位数
数量（箱）	2	1	7	$\text{[math]}$	3	1	4.75	$\text{[math]}$	$\text{[math]}$

（1）直接写出上述表格中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的值；
（2）平均数、众数、中位数都能反映这组数据的集中趋势，请根据以上样本数据分析的结果，任意选择其中一个统计量，估算这 $\text{[math]}$ 箱荔枝共损坏了多少千克？
（3）根据（2）中的结果，求该公司销售这批荔枝每千克定为多少元才不亏本？（结果保留一位小数）

答案解析收藏纠错 + 选题

24. (2021·台州) 杨梅果实成熟期正值梅雨季节，雨水过量会导致杨梅树大量落果，给果农造成损失.为此，市农科所开展了用防雨布保护杨梅果实的实验研究.在某杨梅果园随机选择40棵杨梅树，其中20棵加装防雨布（甲组），另外20棵不加装防雨布（乙组）.在杨梅成熟期，统计了甲、乙两组中每一棵杨梅树的落果率（落地的杨梅颗数占树上原有杨梅颗数的百分比），绘制成如下统计图表（数据分组包含左端值不包含右端值）.

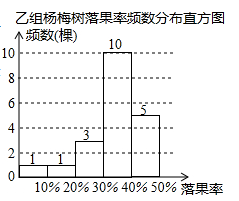
甲组杨梅树落果率频数分布表

落果率	组中值	频数（棵）
0≤x＜10%	5%	12
10%≤x＜20%	15%	4
20%≤x＜30%	25%	2
30%≤x＜40%	35%	1
40%≤x＜50%	45%	1

（1）甲、乙两组分别有几棵杨梅树的落果率低于20%？
（2）请用落果率的中位数或平均数，评价市农科所“用防雨布保护杨梅果实”的实际效果；
（3）若该果园的杨梅树全部加装这种防雨布，落果率可降低多少？说出你的推断依据.

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中