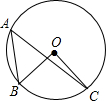

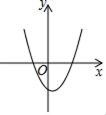
 B .
B .  C .
C .  D .
D . 



并说明理由.

|
时间 x(天) |
1≤x<50 |
50≤x≤90 |
|
售价(元/件) |
x+40 |
90 |
|
每天销量(件) |
200-2x |
|
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
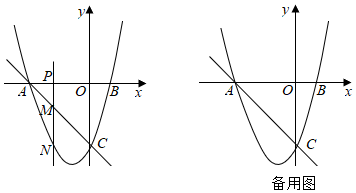
②若点P在x轴上运动,则在y轴上是否存在点Q,使以M,N,C,Q为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.

①求证:EB=EG;
②若CE=5,AC=8,求FG+FB的值.