浙江省丽水市莲都区文元教育集团2022-2023学年九年级上...

更新时间：2024-07-29 浏览次数：119 类型：期中考试

一、选择题（本题有10个小题，每小题3分，共30分）

1. (2022九上·莲都期中) 已知⊙O的半径为3，点P到圆心O的距离为4，则点P（）

A . 在⊙O内 B . 在⊙O上 C . 在⊙O外 D . 无法确定

答案解析收藏纠错 + 选题
2. (2022九上·莲都期中) 下列事件中，属于必然事件的是（）

A . 任意抛掷一只纸杯，杯口朝下 B . 任选三角形的两边，其差小于第三边 C . 打开电视，正在播放动画片 D . 在一个没有红球的袋中摸球，摸出红球

答案解析收藏纠错 + 选题
3. (2022九上·莲都期中) 将抛物线y＝2x²向左平移3个单位，再向上平移5个单位，得到的抛物线的表达式为（）

A . y＝2（x-3）²-5 B . y＝2（x+3）²-5 C . y＝2（x-3）²+5 D . y＝2（x+3）²+5

答案解析收藏纠错 + 选题
4. (2022九上·莲都期中) 在一个不透明的口袋中，放置3个黄球，1个红球和 $\text{[math]}$ 个蓝球，这些小球除颜色外其余均相同，课外兴趣小组每次摸出一个球记录下颜色后再放回，并且统计了蓝球出现的频率（如图所示），则 $\text{[math]}$ 的值最可能是（）

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
5. (2022九上·莲都期中) 如图，在平面直角坐标系中，将点P（2，3）绕原点O顺时针旋转90°得到点P'，则P'的坐标为（）

A . （3，-2） B . （3，-1） C . （2，-3） D . （3，2）

答案解析收藏纠错 + 选题
6. (2022九上·莲都期中) 如图，二次函数y＝a（x+1）²+k的图象与x轴交于A（-3，0），B两点，下列说法错误的是（）

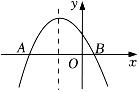
A . a＜0 B . 当x＜0时，y随x的增大而增大 C . 点B的坐标为（1，0） D . 图象的对称轴为直线x＝-1

答案解析收藏纠错 + 选题
7. (2024·雅安模拟) 如图，四边形ABCD内接于 $\text{[math]}$ ，若四边形ABCO是菱形，则 $\text{[math]}$ 的度数为（）

A . 45° B . 60° C . 90° D . 120°

答案解析收藏纠错 + 选题
8. (2022九上·莲都期中) 已知（-3，y₁），（0，y₂），（3，y₃）是抛物线y＝-3x²+6x-k上的点，则（）

A . y₁＜y₃＜y₂ B . y₁＜y₂＜y₃ C . y₃＜y₁＜y₂ D . y₂＜y₁＜y₃

答案解析收藏纠错 + 选题
9. (2022九上·莲都期中) 如图△ABC中，∠ACB＝90°，AC+BC＝8，分别以AB、AC、BC为半径作半圆，若记图中阴影部分的面积为y，AC为x，则下列y关于x的图象中正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2022九上·莲都期中) 如图，抛物线y＝ $\text{[math]}$ x²-4与x轴交于A、B两点，P是以点C（0，3）为圆心，2为半径的圆上的动点，Q是线段PA的中点，连接OQ，则线段OQ的最大值是（）

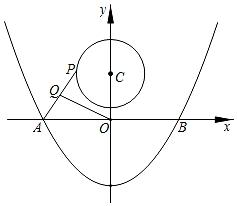
A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题

二、填空题（本题有6个小题，每小题4分，共24分）

11. (2022九上·莲都期中) 若一个圆的半径是6cm，则90度的圆心角所对的弦的长度为.

答案解析收藏纠错 + 选题
12. (2024九下·泰山模拟) 某人连续抛掷一枚质地均匀的硬币10次，结果都是正面朝上，则他第11次抛掷这枚硬币，正面朝上的概率是 .

答案解析收藏纠错 + 选题
13. (2022九上·莲都期中) 如图，A、B、C、D为一个正多边形的相邻四个顶点，O为正多边形的中心，若∠ADB＝12°，则这个正多边形的边数为 .

答案解析收藏纠错 + 选题
14. (2022九上·莲都期中) 已知二次函数y＝x²-2x-2022的图象上有两点A（a，-1）和B（b，-1），则a²+2b-3的值等于 .

答案解析收藏纠错 + 选题
15. (2022九上·莲都期中) ⊙O的半径为10cm，弦AB∥CD，AB＝12cm，CD＝16cm，则AB与CD的距离为.

答案解析收藏纠错 + 选题
16. (2022九上·莲都期中) 如图，C，D是以AB为直径的半圆周上的两点，且AB＝8cm，弧 $\text{[math]}$ 的度数为60°，线段AC，AD与弧CD围成了图中的阴影部分.
1. （1）当CD∥AB时，图中阴影部分的面积为cm²；
2. （2）当C，D在半圆上运动时，阴影部分的最大面积为cm².
答案解析收藏纠错 + 选题

三、解答题（第17、18、19、20题每题8分；21题每题10分；第22、23题12分，共66分）

17. (2022九上·莲都期中) 如图，已知抛物线y＝-x²+mx+5与x轴交于A，B两点，与y轴交于点C，点B的坐标为（5，0）.
1. （1）求m的值及抛物线的顶点坐标.
2. （2）点P是抛物线对称轴l上的一个动点，当PA+PC的值最小时，求点P的坐标.
答案解析收藏纠错 + 选题
18. (2022九上·舟山月考) 当前疫情防控形势严峻，为确保校园平安，某校严格落实测体温进校园的防控要求.每天早上进校园开设了甲，乙，丙三个测温通道.某天早晨，小明和小丽两位同学随机通过测温通道进入校园.
1. （1）求小明从甲测温通道通过的概率.
2. （2）利用画树状图或列表的方法，求小明和小丽从同一个测温通道通过的概率.
答案解析收藏纠错 + 选题
19. (2022九上·莲都期中) 如图1，要利用一面墙（墙长为15m）建羊圈，用30m的围栏围成两个大小相同的矩形羊圈，设羊圈的一边AB长为xm，羊圈总面积为ym².
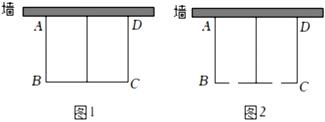
1. （1）请问能否围成总面积为81m²的羊圈，若能，请求出AB的长；若不能，请说明理由.
2. （2）如果两个矩形羊圈各开一个宽1m的门（如图2），在不浪费围栏的情况下，求y与x的函数关系式并写出x的取值范围，求出羊圈总面积最大值.
答案解析收藏纠错 + 选题
20. (2022九上·莲都期中) 如图所示，在△ABC中，AB＝AC，⊙O是△ABC的外接圆，BO的延长线交边AC于点D.
1. （1）若∠ACB＝60°，BC＝8 $\text{[math]}$ ，求⊙O的半径；
2. （2）当△BCD是等腰三角形时，求∠BCD的大小.
答案解析收藏纠错 + 选题
21. (2022九上·莲都期中) 我们在学习了《浙教版数学九年级上册》P17探究活动，“已知：如图为一座拱桥的示意图，当水面宽为12m时，桥洞顶部离水面4m已知桥洞的拱形是抛物线”，现以水平方向AB为x轴，若小明同学以C为顶点求出了函数表达式是 $\text{[math]}$ ；

探究一：
1. （1）若小红同学以A为顶点求出了函数表达式是 .
2. （2）在（1）条件下，求出该抛物线在水面AB中的倒影所在抛物线函数表达式为 .
3. （3）一艘宽为4米，高出水面3米的货船，能否从桥下通过？
4. （4）探究二：
  若已知桥洞的拱形是圆的一部分，当水面宽为12m时，桥洞顶部离水面4m，该圆半径为 .
答案解析收藏纠错 + 选题
22. (2022九上·莲都期中) 已知，点M为二次函数y＝-（x-b）²+4b+1图象的顶点，直线y＝mx+5分别交x轴正半轴，y轴于点A，B.
1. （1）判断顶点M是否在直线y＝4x+1上，并说明理由.
2. （2）如图1，若二次函数图象也经过点A，B，且mx+5＞-（y-b）²+4b+1，根据图象，写出x的取值范围.
3. （3）如图2，点A坐标为（5，0），点M在△AOB内，若点C（ $\text{[math]}$ ， y₁），D（ $\text{[math]}$ ， y₂）都在二次函数图象上，试比较y₁与y₂的大小.
答案解析收藏纠错 + 选题
23. (2022九上·莲都期中) 如图，△ABC是⊙O的内接三角形，AC＝BC，D为⊙O的弧AB上一点，延长DA至点E，使CE＝CD.
1. （1）求证：AE＝BD；
2. （2）若AC⊥BC，试说明AD、BD与CD之间是否存在某种确定的等量关系？请画图（非尺规作图），写出你的结论并证明.
3. （3）若AD+BD＝ $\text{[math]}$ CD，则∠ACB＝.
答案解析收藏纠错 + 选题