①对角线相等且互相平分的四边形是矩形②对角线互相垂直的四边形是菱形③四边相等的四边形是正方形④四边相等的四边形是菱形
①三角形三条高相交于一点;②两边和一角对应相等的两个三角形全等;③有一个角是 , 并且两腰分别相等的两个等腰三角形全等;④到三角形三个顶点距离相等的点是三角形三条角平分线的交点;⑤等腰三角形一腰上的高与底边的夹角等于顶角的一半.其中正确的有( )
②一个角的补角大于这个角;
③两直线平行,同位角相等;
④有两边和其中一边的对角对应相等的两个三角形全等;
⑤点P坐标为(-2,6),将其先向右平移6个单位,再向下平移8个单位,得到点P1 , 坐标为(4,-2).
其中是真命题的有.

已知:在锐角中,
, ▲ ;
求证: ▲ .
已知:如图,在四边形ABCD中,
BC=AD,
AB=.
求证:四边形ABCD是四边形.
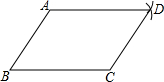
证明:

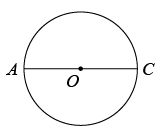
已知:如图, .
求作:矩形 ,使矩形
内接于
,对角线
与
的夹角为
作法:①作 的直径
;
②以点A为圆心, 长为半径作弧.交直线
上方的圆于点B;
③连接 并延长交
于点D;
④顺次连接 、
、
和
.
四边形 就是所求作的矩形,
根据小明设计的尺规作图过程
证明:∵点A,C都在 上,
,
.
∴四边形 是平行四边形.( )(填推理依据).
又 是
的直径,
( )(填推理依据).
∴四边形 是矩形.
又 ▲ .
是等边三角形.
∴四边形 是所求作的矩形.

①互补三角形一定不全等.命题
②互补三角形的面积相等.命题
求证:;
小聪学完了“锐角三角函数”的相关知识后,通过研究发现:如图1,在Rt△ABC中,如果∠C=90°,∠=30°,BC═a=1,AC=b= , AB=c=2,那么
=
=2.通过上网查阅资料,他又知“sin90°=1”,因此他得到“在含30°角的直角三角形中,存在着
=
=
的关系.
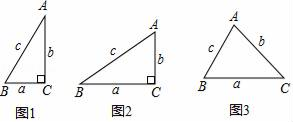
这个关系对于一般三角形还适用吗?为此他做了如下的探究:
如图3,在锐角△ABC中,BC=a,AC=b,AB=c,请判断此时“ =
=
”的关系是否成立?并证明你的判断.(提示:过点C作CD⊥AB于D,过点A作AH⊥BC,再结合定义或其它方法证明).