2023年浙教版数学七年级下册全方位训练卷第四章因式分解（...

更新时间：2023-02-19 浏览次数：206 类型：单元试卷

一、单选题（每题3分，共30分）

1. (2019八上·浦东期中) 下列二次三项式在实数范围内不能因式分解的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021七下·余姚竞赛) 已知 $\text{[math]}$ 加上一个单项式后能成为一个整式的完全平方，给出下面四个单项式① $\text{[math]}$ ， ② $\text{[math]}$ ， ③ $\text{[math]}$ 1 ， ④ $\text{[math]}$ ，其中满足条件的共有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
3. (2019八下·鼓楼期末) 计算3×（ $\text{[math]}$ ﹣2018×（ $\text{[math]}$ ）+1的结果等于（　　）

A . ﹣2017 B . ﹣2018 C . ﹣2019 D . 2019

答案解析收藏纠错 + 选题
4. 已知a为实数，且a³+a²-a+2=0，则（a+1）²⁰⁰⁸+（a+1）²⁰⁰⁹+（a+1）²⁰¹⁰的值是（）

A . -3 B . 3 C . -1 D . 1

答案解析收藏纠错 + 选题
5. (2021七上·青岛期中) 下列各式中，不能由m-n+c通过变形得到的是（）

A . m-(n-c) B . c-(n-m) C . m-(n+c) D . (m-n)+c

答案解析收藏纠错 + 选题
6. (2021八上·泰安期中) 计算-2²⁰²¹+(-2)²⁰²⁰所得的结果是（）

A . -2²⁰²⁰ B . -2²⁰²¹ C . 2²⁰²⁰ D . -2

答案解析收藏纠错 + 选题
7. (2022八上·无为月考) 在多项式 $\text{[math]}$ 添加一个单项式，使得到的多项式能运用完全平方公式分解因式，则下列表述正确的是（　　）
嘉琪：添加 $\text{[math]}$ ， $\text{[math]}$ ；
陌陌：添加 $\text{[math]}$ ， $\text{[math]}$ ；
嘟嘟：添加 $\text{[math]}$ ， $\text{[math]}$ ．

A . 嘉琪和陌陌的做法正确 B . 嘉琪和嘟嘟的做法正确 C . 陌陌和嘟嘟的做法正确 D . 三位同学的做法都正确

答案解析收藏纠错 + 选题
8. 若多项式9x²+mx+1是完全平方式，则符合条件的所有ｍ的值为（）

A . ±6 B . －6 C . 6 D . ±18

答案解析收藏纠错 + 选题
9. (2022·包头) 已知实数a，b满足 $\text{[math]}$ ，则代数式 $\text{[math]}$ 的最小值等于（）

A . 5 B . 4 C . 3 D . 2

答案解析收藏纠错 + 选题
10. (2020七下·温州期中) 如图，在长方形 ABCD 中，E 为 AB 中点，以 BE 为边作正方形 BEFG，边 EF 交 CD 于点H，在边 BE 上取点 M 使BM=BC，作 MN∥BG 交 CD 于点 L，交 FG 于点 N．

欧几里得在《几何原本》中利用该图解释了 $\text{[math]}$ ，连结AC，记△ABC的面积为 $\text{[math]}$ ，图中阴影部分的面积为 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每题3分，共18分）

11. (2022七下·江阴期中) 多项式 $\text{[math]}$ 加上一个单项式后，可化为一个整式的平方，则这个单项式是.（写一个即可）

答案解析收藏纠错 + 选题
12. 请从4a² ，（x+y）² ， 1，9b²中，任选两式做差得到的一个式子进行因式分解是

答案解析收藏纠错 + 选题
13. 将xⁿ﹣yⁿ分解因式的结果为（x²+y²）（x+y）（x﹣y），则n的值为

答案解析收藏纠错 + 选题
14. (2021·宣城模拟) 已知 $\text{[math]}$ 为实数，若 $\text{[math]}$ 均为多项式 $\text{[math]}$ 的因式，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2019七上·徐汇期中) 甲乙两个同学分解因式x²+ax+b时，甲看错了b ，分解结果为（x+2）（x+4），乙看错了a ，分解结果为（x+1）（x+9），则2a+b＝．

答案解析收藏纠错 + 选题
16. (2019七下·嘉兴期末) 在日常生活中如取款、上网等都需要密码，有一种用“因式分解法”产生的密码，方便记忆，原理是对于多项x⁴-y⁴ ，因式分解的结果是(x-y)(x+y)(x²+y²)，若取x=9，y=9时，则各个因式值是：(x+y)=18，(x-y)=0，(x²+y²)=162,于是就可以把“180162”作为一个六位数的密码，对于多项式9x³-xy² ，取x=10，y=10时，用上述方法产生的密码是(写出一个即可).

答案解析收藏纠错 + 选题

三、计算题（共2题，共12分）

17. (2020八上·红安月考) 计算题：
1. （1）因式分解：（x²+y²）²-4x²y²；
2. （2）计算：8（1+7²）（1+7⁴）（1+7⁸）（1+7¹⁶）.
答案解析收藏纠错 + 选题
18. 简便计算：
1. （1） $\text{[math]}$ .
2. （2） $\text{[math]}$ .
答案解析收藏纠错 + 选题

四、解答题

19. 观察下列各式：(1)－a＋b＝－(a－b)；(2)2－3x＝－(3x－2)；(3)5x＋30＝5(x＋6)；(4)－x－6＝－(x＋6)．探索以上四个式子中括号的变化情况，思考它和去括号法则有什么不同．利用你探索出来的规律，解答下面的题目：
已知a²－b²＝5，1－b＝－2，求1＋a²＋b－b²的值．

答案解析收藏纠错 + 选题
20. (2022七下·绍兴期中) 阅读下面例题，并解答问题。
例题：已知二次三项式 $\text{[math]}$ 有一个因式是 $\text{[math]}$ ，求另一个因式以及m的值

解：设另一个因式为 $\text{[math]}$ ，得 $\text{[math]}$

则 $\text{[math]}$ ∴ $\text{[math]}$ 解得： $\text{[math]}$ ， $\text{[math]}$

∴另一个因式为 $\text{[math]}$ ，m的值为—21

请仿照上面的方法解答下面的问题：

已知二次三项式 $\text{[math]}$ 有一个因式是 $\text{[math]}$ ，求另一个因式以及k的值。

答案解析收藏纠错 + 选题
21. (2019七下·鄞州期末) 已知：a-b=m，b-c=n．
1. （1） m=3，n=4，求代数式（a-c)² ， a²+b²+c²-ab-bc-ca的值。
2. （2）若m<0，n<0，判断代数 $\text{[math]}$ 的值与0的大小关系并说明理由．
答案解析收藏纠错 + 选题
22. 阅读理解：
对于二次三项式 $\text{[math]}$ ，能直接用公式法进行因式分解，得到 $\text{[math]}$ ，但对于二次三项式 $\text{[math]}$ ，就不能直接用公式法了.

我们可以求用这样的方法：在二次三项式 $\text{[math]}$ $\text{[math]}$ 中先加上一项 $\text{[math]}$ ，使其成为完全平方式，再减去 $\text{[math]}$ 这项，使整个式了的值不变，于是：

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

像这样把二次三项式分解因式的方法叫做添(拆)项法.
1. （1）问题解决：请用上述方法将二次三项式x²＋2ax—3a²分解因式；
2. （2）拓展应用：二次三项式x²-4x＋5有最小值或最大值吗？如果有，请你求出来并说明理由.
答案解析收藏纠错 + 选题
23. (2020八上·大理期末)
1. （1）填空： $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ ；
2. （2）阅读，并解决问题：分解因式 $\text{[math]}$
  解：设 $\text{[math]}$ ，则原式 $\text{[math]}$
  
  这样的解题方法叫做“换元法”，即当复杂的多项式中，某一部分重复出现时，我们用字母将其替换，从而简化这个多项式，换元法是一个重要的数学方法，不少问题能用换元法解决.请你用“换元法”对下列多项式进行因式分解：
  
  ① $\text{[math]}$
  
  ② $\text{[math]}$
答案解析收藏纠错 + 选题
24. (2021八上·镇原期末) 阅读材料
小明遇到这样一个问题：求计算（x+2）（2x+3）（3x+4）所得多项式的一次项系数．

小明想通过计算（x+2）（2x+3）（3x+4）所得的多项式解决上面的问题，但感觉有些繁琐，他想探寻一下，是否有相对简洁的方法．

他决定从简单情况开始，先找（x+2）（2x+3）所得多项式中的一次项系数．通过观察发现：

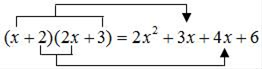
也就是说，只需用x+2中的一次项系数1乘以2x+3中的常数项3，再用x+2中的常数项2乘以2x+3中的一次项系数2，两个积相加1×3+2×2=7，即可得到一次项系数．

延续上面的方法，求计算（x+2）（2x+3）（3x+4）所得多项式的一次项系数．可以先用x+2的一次项系数1，2x+3的常数项3，3x+4的常数项4，相乘得到12；再用2x+3的一次项系数2，x+2的常数项2，3x+4的常数项4，相乘得到16；然后用3x+4的一次项系数3，x+2的常数项2，2x+3的常数项3，相乘得到18．最后将12，16，18相加，得到的一次项系数为46．

参考小明思考问题的方法，解决下列问题：
1. （1）计算（2x+1）（3x+2）所得多项式的一次项系数为．
2. （2）计算（x+1）（3x+2）（4x﹣3）所得多项式的一次项系数为．
3. （3）若计算（x²+x+1）（x²﹣3x+a）（2x﹣1）所得多项式的一次项系数为0，则a=．
4. （4）若x²﹣3x+1是x⁴+ax²+bx+2的一个因式，则2a+b的值为．
答案解析收藏纠错 + 选题
25. (2020八上·朔城月考) 综合与实践
下面是某同学对多项式 $\text{[math]}$ 进行因式分解的过程：

解：设 $\text{[math]}$ ，

原式 $\text{[math]}$ （第一步）

$\text{[math]}$ （第二步）

$\text{[math]}$ （第三步）

$\text{[math]}$ （第四步）．

回答下列问题：
1. （1）该同学第二步到第三步运用了________．
  
  A . 提取公因式 B . 平方差公式 C . 两数差的完全平方公式 D . 两数和的完全平方公式
2. （2）该同学因式分解的结果是否彻底？（填“彻底”或“不彻底”），若不彻底，则该因式分解的最终结果为．
3. （3）请你模仿上述方法，对多项式 $\text{[math]}$ 进行因式分解．
答案解析收藏纠错 + 选题
26. (2022七下·北仑期中) 我们知道，任意一个正整数c都可以进行这样的分解：c=a×b（a．b是正整数，且a≤b），在c的所有这些分解中，如果a，b两因数之差的绝对值最小，我们就称a×b是c的最优分解并规定：M（c）= $\text{[math]}$ ，例如9可以分解成1×9，3×3，因为9-1＞3-3，所以3×3是9的最优分解，所以M（9）= $\text{[math]}$ =1
1. （1）求M（8）；M（24）；M[（c+1）²]的值；
2. （2）如果一个两位正整数d（d=10x+y ， x ， y都是自然数，且1≤x≤y≤9），交换其个位上的数与十位上的数得到的新数加上原来的两位正整数所得的和为66，那么我们称这个数为“吉祥数”，求所有“吉祥数”中M（d）的最大值．
答案解析收藏纠错 + 选题