2023年苏科版数学八年级下册全方位训练卷9.5三角形的中位...

更新时间：2023-02-23 浏览次数：57 类型：同步测试

一、单选题（每题3分，共24分）

1. (2022八下·盐城期末) 如图，D、E、F是△ABC各边的中点，若△ABC的周长为12，则△DEF的周长为（）

A . 2 B . 4 C . 6 D . 8

答案解析收藏纠错 + 选题
2. (2022八下·江都期中) 如图，菱形ABCD的对角线AC，BD相交于点O， $\text{[math]}$ ， $\text{[math]}$ ，点E为BC的中点，则OE的长为（）

A . 2.5 B . 3 C . 5 D . 6

答案解析收藏纠错 + 选题
3. (2022八下·连云期中) 若顺次连接四边形各边中点所得的四边形是菱形，则原四边形（）

A . 一定是矩形 B . 一定是菱形 C . 对角线一定互相垂直 D . 对角线一定相等

答案解析收藏纠错 + 选题
4. (2023八下·江都期末) 如图，A、B两地被池塘隔开，小强通过下面的方法估测出A、B间的距离：先在AB外选一点C，然后步测出AC、BC的中点D、E，并且步测出DE长，由此推算出AB长.若步测DE的长为50m，则A、B间的距离是（）

A . 25m B . 50m C . 75m D . 100m

答案解析收藏纠错 + 选题
5. (2021九上·金台期末) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ 分别是 $\text{[math]}$ 的中点，要使四边形 $\text{[math]}$ 是矩形，则四边形 $\text{[math]}$ 只需要满足一个条件是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020八下·抚顺期末) 如图，在四边形ABCD中，∠A=90°，AB=3， $\text{[math]}$ ，点M、N分别为线段BC、AB上的动点，点E、F分别为DM、MN的中点，则EF长度的最大值为（）

A . 2 B . 3 C . 4 D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020八下·灌云月考) 如图所示，在四边形 $\text{[math]}$ 中，点 $\text{[math]}$ 是对角线 $\text{[math]}$ 的中点，点 $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 的中点， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（　　）

A . 15° B . 20° C . 25° D . 30°

答案解析收藏纠错 + 选题
8. (2022八上·莱州期末) 如图所示，吴伯伯家一块等边三角形的空地ABC，已知点E，F分别是边AB，AC的中点，量得EF=5米，他想把四边形BCFE用篱笆围成一圈放养小鸡，则需要篱笆的长是（）

A . 15米 B . 20米 C . 25米 D . 30米

答案解析收藏纠错 + 选题

二、填空题（每题3分，共24分）

9. (2022八下·邗江期末) 如图，点E在平行四边形ABCD的边AD上，且AE＝2ED，M、N分别是BE、CE的中点，连接MN，已知MN＝3，则AE的长是.

答案解析收藏纠错 + 选题
10. (2022八下·常熟期末)
如图， $\text{[math]}$ ， $\text{[math]}$ 分别为矩形 $\text{[math]}$ 的边 $\text{[math]}$ ， $\text{[math]}$ 的中点，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为.

答案解析收藏纠错 + 选题
11. (2021八下·梁溪期末) $\text{[math]}$ 中， $\text{[math]}$ 分别为 $\text{[math]}$ 的中点，若 $\text{[math]}$ 则 $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2021八下·丹徒期末) 如图，在△ABC中，∠ACB＝90°，AB＝10cm，BC＝8cm，点D在边AB上，AD＝AC，AE⊥CD，垂足为E，点F是BC的中点，则EF＝cm.

答案解析收藏纠错 + 选题
13. (2021八下·江都期末) 如图，A，B两点被池塘隔开，不能直接测量其距离.于是小明在岸边选一点C，连接CA，CB，分别延长到点M，N，使AM=AC，BN=BC，测得MN=20m，则A，B间的距离为m.

答案解析收藏纠错 + 选题
14. (2021八下·江阴期末) 如图，在平行四边形 $\text{[math]}$ 中，对角线 $\text{[math]}$ 、 $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边的中点， $\text{[math]}$ 、 $\text{[math]}$ 为 $\text{[math]}$ 上的点，连接 $\text{[math]}$ 和 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则图中阴影部分的面积为.

答案解析收藏纠错 + 选题
15. (2022八下·沈北期末) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 边上，点 $\text{[math]}$ 为 $\text{[math]}$ 边上的动点，点 $\text{[math]}$ 、 $\text{[math]}$ 分别为 $\text{[math]}$ ， $\text{[math]}$ 的中点，则 $\text{[math]}$ 的最小值是.

答案解析收藏纠错 + 选题
16. (2021八下·海州期末) 如图，已知点 $\text{[math]}$ 在正方形 $\text{[math]}$ 的边 $\text{[math]}$ 上，以 $\text{[math]}$ 为边向正方形 $\text{[math]}$ 外部作正方形 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 的中点，连接 $\text{[math]}$ .若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题

三、解答题（共10题，共72分）

17. (2020八下·秦淮期末) 如图，四边形ABCD是菱形，E、F、G、H分别是边AB、BC、CD、DA的中点，连接EF、FG、GH、HE.求证：四边形EFGH是矩形.

答案解析收藏纠错 + 选题
18. (2019八下·邳州期中) 如图，在平行四边形ABCD中，EF∥AB且交BC于点E，交AD于点F，连接AE、BF交于点M，连接CF、DE交于点N，连接MN.试探讨MN与AD的大小关系和位置关系，并加以证明.

答案解析收藏纠错 + 选题
19. (2019八下·苏州期中) 如图，在四边形ABCD中，E、F分别是AD、BC的中点，G、H分别是BD、AC的中点且AB=CD，则EF与GH有怎样的关系？请说明你的理由.

答案解析收藏纠错 + 选题
20. (2022八下·无为期末) 如图，在 $\text{[math]}$ 中，D，E，F分别是AB，BC，CA的中点， $\text{[math]}$ ， $\text{[math]}$ ，求四边形DECF的周长．

答案解析收藏纠错 + 选题
21. (2022八下·大丰期中) 如图，DE是△ABC的中位线，过点C作CF∥AB，交DE的延长线于点F．
1. （1）求证：BC＝DF；
2. （2）连接CD、AF，当△ABC满足什么条件时，四边形ADCF是矩形，请说明理由．
答案解析收藏纠错 + 选题
22. (2022八下·威县期末) 如图，在 $\text{[math]}$ 中，点D，点E分别是边AC，AB的中点，点F在线段DE上， $\text{[math]}$ 交BC于点G．
1. （1）证明：四边形EFGB是菱形；
2. （2）若 $\text{[math]}$ ，求DF的长度．
答案解析收藏纠错 + 选题
23. (2022八下·定远期末) 如图，在▱ABCD中，点E在边AD上，连接EB并延长至F，使BF＝BE；连接EC并延长至G，使CG＝CE，连接FG，点H为FG的中点，连接DH，AF．
1. （1）若∠BAE＝70°，∠DCE＝20°，求∠DEC的度数；
2. （2）求证：四边形AFHD为平行四边形．
答案解析收藏纠错 + 选题
24. (2021八下·兴化期末) 如图1，在四边形 $\text{[math]}$ 中， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的中点.
1. （1）求证：四边形 $\text{[math]}$ 是平行四边形；
2. （2）如图2，延长 $\text{[math]}$ 、 $\text{[math]}$ 相交于点 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，若 $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
25. (2021八下·姜堰期中) 如图，已知四边形ABCD是正方形.
1. （1）如图1，若E、F、G分别是AB、BC、CD边上的点，AF和EG交于点O.现在提供三个关系：①AF⊥EG；②AO＝FO；③AF＝EG.从三个关系中选择一个作为条件，一个作为结论，形成一个真命题，完成下列填空并证明：你选择的条件是，结论是.（只要填写序号）.
2. （2）如图2，点E、F分别在AD、AB上，BE⊥CF，垂足为点O，连接EF、EC，M、N分别是BF、CE的中点，MN分别交BE、CF于点G、H，求证：OG＝OH；
3. （3）如图3，AB＝3cm，E为CD边上一点，∠DAE=30°，O为AE的中点，过点O的直线分别交AD、BC于点M、N，若MN＝AE，请直接写出AM的长.
答案解析收藏纠错 + 选题
26. (2020八下·秦淮期末) 我们知道，平行四边形的对边平行且相等.利用这一性质，可以为证明线段之间的位置关系和数量关系提供帮助.
1. （1）重温定理，识别图形
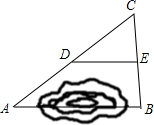
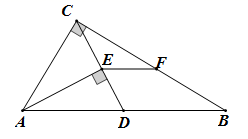
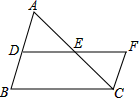
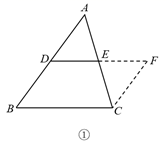
  如图①，我们在探究三角形中位线DE和第三边BC的关系时，所作的辅助线为“延长DE到点F，使EF＝DE，连接CF”，此时DE与DF在同一直线上且DE= $\text{[math]}$ DF，又可证图中的四边形为平行四边形，可得BC与DF的关系是，于是推导出了“DE $\text{[math]}$ BC，DE＝ $\text{[math]}$ BC”.
2. （2）寻找图形，完成证明
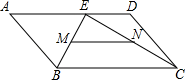
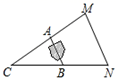
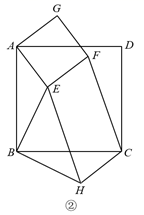
  如图②，四边形ABCD和四边形AEFG都是正方形，△BEH是等腰直角三角形，∠EBH＝90°，连接CF、CH.求证CF＝ $\text{[math]}$ BE.
3. （3）构造图形，解决问题
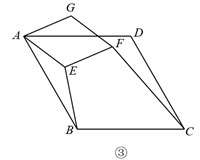
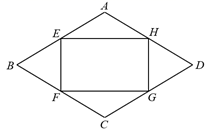
  如图③，四边形ABCD和四边形AEFG都是菱形，∠ABC＝∠AEF＝120°，连接BE、CF.直接写出CF与BE的数量关系.
答案解析收藏纠错 + 选题