① ;②
;③
;④
;⑤
.
其中正确的是( )

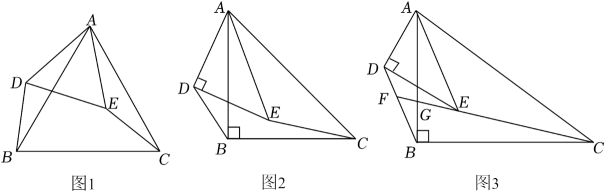
①求的值;
②延长CE交BD于点F,交AB于点G.求sin∠BFC的值.
一次数学综合实践活动课上,小慧发现并证明了关于三角形角平分线的一个结论.如图1,已知AD是△ABC的角平分线,可证=
.小慧的证明思路是:如图2,过点C作CE∥AB,交AD的延长线于点E,构造相似三角形来证明
=
.

①若AC=1,AB=2,求DE的长;
②若BC=m,∠AED= , 求DE的长(用含m,
的式子表示).
小明不完整的证明过程如下,请你帮他补充完整.
证明:如图,在BA上截取BH=BE,连接EH.
∵k=2, ∴AB=BC. ∵∠B=90°,BH=BE, ∴∠1=∠2=45°, ∴∠AHE=180°-∠1=135°. ∵CF平分∠DCG,∠DCG=90°, ∴∠3= ∴∠ECF=∠3+∠4=135°. ∴…… (只需在答题卡对应区域写出剩余证明过程) |