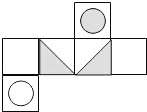
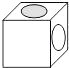
 B .
B . 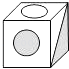 C .
C . 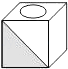 D .
D . 


日期 | 1.10 | 1.11 | 1.12 | 1.13 | 1.14 | 1.15 | 1.16 |
得分 | 62 | 49 | 55 | 45 | 55 | 48 | 55 |
则这组数据的众数为.


购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上(含91套) |
每套服装的价格 | 60元 | 50元 | 40元 |

根据以上信息, 回答下列问题:




特例探索:
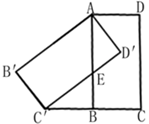
②如图2,当 ,
时,求a和b的值.
请你观察(1)中的计算结果,猜想三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.