 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C .  D .
D . 
①;②
③
④直线
可能与
有4个交点
⑤若点 , 点
是抛物线上的两点,若
, 则
.
其中正确的有( )








①求与t的函数关系式(不写t的取值范围);
②当甲赶到排头位置时,求的值;在甲从排头返回到排尾过程中,设甲与位置O的距离为
, 求
与t的函数关系式(不写t的取值范围)
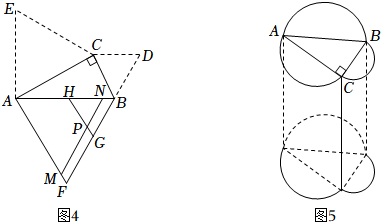
如图,中,
.
下图为该兴趣小组绘制的赛道截面图,以停止区CD所在水平线为x轴,过起跳点A与x轴垂直的直线为y轴,O为坐标原点,建立平面直角坐标系.着陆坡AC的坡角为30°, . 某运动员在A处起跳腾空后,飞行至着陆坡的B处着陆,
. 在空中飞行过程中,运动员到x轴的距离
与水平方向移动的距离
具备二次函数关系,其解析式为
.

①求x关于t的函数解析式;
②当t为何值时,运动员离着陆坡的竖直距离h最大,最大值是多少?
