浙江省湖州市南浔区2023年中考一模数学试题

更新时间：2024-07-13 浏览次数：200 类型：中考模拟

一、单选题

1. (2023·南浔模拟) 3的相反数是（）.

A . $\text{[math]}$ B . 3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·南浔模拟) 下列图案是历届冬奥会会徽，其中是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023·南浔模拟) 截止2023年2月，全国学习强国注册用户总数超过257000000人，数257000000用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九下·西安模拟) 在我县“我的中国梦”演讲比赛中，有7名同学参加了比赛，他们最终决赛的成绩各不相同．其中一名学生想要知道自己是否进入前3名，不仅要知道自己的分数，还得知道这7名学生成绩的（）

A . 众数 B . 方差 C . 平均数 D . 中位数

答案解析收藏纠错 + 选题
6. (2024八上·浙江期末) 通过如下尺规作图，能确定点D是BC边中点的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2023·南浔模拟) 若 $\text{[math]}$ ，则下列各式中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024七下·兰考期末) 我国古代数学著作《孙子算经》有“多人共车”问题：“今有三人共车，二车空；二人共车，九人步，问：人与车各几何？”其大意如下：有若干人要坐车，如果每3人坐一辆车，那么有2辆空车；如果每2人坐一辆车，那么有9人需要步行，问人与车各多少？设共有x人，y辆车，则可列方程组为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023·南浔模拟) 甲，乙两人同时从相距90千米的A地前往B地，甲乘汽车，乙骑电动车，甲到达B地停留半个小时后返回A地，如图是他们离A地的距离y（千米）与经过时间x（小时）之间的函数关系图象.当甲与乙相遇时距离A地（）

A . 16千米 B . 18千米 C . 72千米 D . 74千米

答案解析收藏纠错 + 选题
10. (2023·南浔模拟) 如图，点P是 $\text{[math]}$ 斜边AB上的动点，点D、E分别在AC、BC边上，连结PD、PE，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则当 $\text{[math]}$ 取得最小值时AP的长是（）

A . 18 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. 计算 $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2024·鄞州模拟) 为减少安全隐患，某学校将一批方角型书桌更换为圆角型书桌.已知此书桌桌角所在圆的半径为5cm，所对的圆心角为90°，则一个桌角的弧长为cm.

答案解析收藏纠错 + 选题
13. 从一盒写有“鲜肉1只，蛋黄2只”的端午粽子（所有粽子的形状大小都一样）礼盒中，随机取出2只粽子，恰好都是蛋黄粽子的概率是.

答案解析收藏纠错 + 选题
14. (2023·郫都模拟) 一根排水管的截面如图所示，已知排水管的半径OB＝5cm，水面宽AB＝8，则截面圆心O到水面的距离OC的长是.

答案解析收藏纠错 + 选题
15. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， D为 $\text{[math]}$ 边上一点，沿 $\text{[math]}$ 将三角形进行折叠，使点A落在点E处，记 $\text{[math]}$ 与 $\text{[math]}$ 边的交点为F，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为.

答案解析收藏纠错 + 选题
16. (2023·南浔模拟) 将一副三角板按如图方式放置在平面直角坐标系中，已知AB＝2，反比例函数 $\text{[math]}$ 的图象恰好经过顶点C，D， $\text{[math]}$ 轴，则k的值为.

答案解析收藏纠错 + 选题

三、解答题

17. (2023·南浔模拟) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
18. 如图，已知在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长和 $\text{[math]}$ 的值

答案解析收藏纠错 + 选题

19. (2023·南浔模拟) 小王和小凌在解答“解分式方程： $\text{[math]}$ ”的过程如下框，请你判断他们的解法是否正确？若错误，请写出你的解答过程.

小王的解法：

解，去分母得： $\text{[math]}$ ①

去括号得： $\text{[math]}$ ②

移项得： $\text{[math]}$ ③

合并同类项得： $\text{[math]}$ ④

系数化为1得： $\text{[math]}$ ⑤

$\text{[math]}$ 是原分式方程的解 ⑥

小凌的解法：

解，去分母得： $\text{[math]}$ ①

移项得： $\text{[math]}$ ②

合并同类项得： $\text{[math]}$ ③

系数化为1得： $\text{[math]}$ ④

$\text{[math]}$ 是原分式方程的解 ⑤

答案解析收藏纠错 + 选题

20. (2023·南浔模拟) 劳动教育是学校贯彻“五育并举”的重要举措，某校倡议学生在家帮助父母做一些力所能及的家务，小杨随机抽取该校部分学生进行问卷调查，问卷调查表如下所示，并根据调查结果绘制了两幅不完整的统计图.
平均每周做家务的时间调查表
设平均每周做家务的时间为x小时，则最符合你的选项是（）（单选）
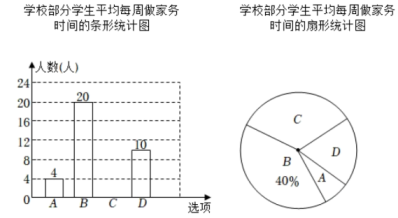
A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$
根据统计图中的信息，解答下列问题：
1. （1）求小杨共调查了多少人和扇形统计图中表示选项“D”的扇形的圆心角度数；
2. （2）将条形统计图补充完整；
3. （3）该校有1500名学生，根据抽样调查结果，请你估计该校平均每周做家务的时间不少于2小时的学生人数.
答案解析收藏纠错 + 选题
21. (2023·南浔模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， D为 $\text{[math]}$ 上的一点，以 $\text{[math]}$ 为直径的半圆与交 $\text{[math]}$ 于点F，且 $\text{[math]}$ 切 $\text{[math]}$ 于点E.
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
22. (2023·南浔模拟) 某校的甲，乙两位老师同住一小区，该小区与学校相距1800米．甲从小区步行去学校，出发10分钟后乙再出发，乙从小区先骑公共自行车，途经学校又骑行若干米到达还车点后，立即以45米/分钟的速度步行到学校，设甲步行的时间为x（分钟），图中线段 $\text{[math]}$ 和折线 $\text{[math]}$ 分别表示甲，乙离开小区的路程y米）与甲步行时间x（分钟）的函数关系的图象，根据图中所给信息，解答下列问题：
1. （1）写出点E横坐标的实际意义，并求出点E的纵坐标．
2. （2）求乙从还车点到学校所花的时间．
3. （3）两人何时相距300米？
答案解析收藏纠错 + 选题
23. (2023·南浔模拟) 单板滑雪大跳台是北京冬奥会比赛项目之一，滑雪大跳台在设计时融入了敦煌壁画中“飞天”的元素，故又名“雪飞天”.图1为“雪飞天”滑雪大跳台赛道的横截面示意图.运动员从D点起跳后到着陆坡 $\text{[math]}$ 着落时的飞行路线可以看作是抛物线的一部分，取水平线 $\text{[math]}$ 为x轴，铅垂线 $\text{[math]}$ 为y轴，建立平面直角坐标示如图2，从起跳到着落的过程中，运动员的铅垂高度y（单位：m）与水平距离x（单位：m）近似满足函数关系 $\text{[math]}$ .在着陆坡 $\text{[math]}$ 上设置点 $\text{[math]}$ 作为标准点，着陆点在K点或超过K点视为成绩达标.
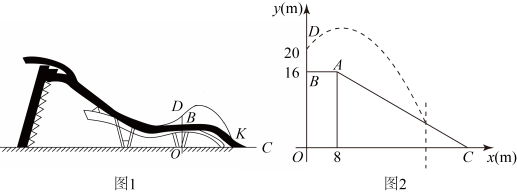
水平距离x（m）
0
2
6
10
14
18
铅垂高度y（m）
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
1. （1）在某运动员的一次试跳中，测得该运动员的水平距离x与铅垂高度y的几组数据如上表，根据上述数据，直接写出该运动员铅垂高度的最大值，并求出满足的函数关系式
2. （2）请问在此次试跳中，该运动员的成绩是否达标？
3. （3）此次试跳中，该运动员在空中从起跳到达最高点的高度或从最高点到下落的高度h（m）与时间t（s）均满足 $\text{[math]}$ （其中g为常数，表示重力加速度，取 $\text{[math]}$ ），运动员要完成“飞天”动作至少在空中要停留3秒钟，问该运动员从起跳到落地能完成动作吗？
答案解析收藏纠错 + 选题
24. (2023·南浔模拟) 如图，在矩形ABCD中，AE平分∠BAD交射线BC于点E，过点C作CF⊥AE交射线AE于点F，连结BD交AE于点G，连结DF交射线BC于点H.
1. （1）当AB＜AD时，
  ①求证：BE＝CD，
  ②猜想∠BDF的度数，并说明理由.
2. （2）若 $\text{[math]}$ 时，求tan∠CDF的值（用含k的代数式表示）.
答案解析收藏纠错 + 选题