吉林省长春市绿园区2023年中考一模数学试题

更新时间：2023-04-29 浏览次数：85 类型：中考模拟

一、单选题

1. (2023·绿园模拟) 不等式 $\text{[math]}$ 的解集在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024·阿克苏模拟) 据统计我国每年浪费的粮食约35000000吨，我们要勤俭节约，反对浪费，积极的加入“光盘行动”中来.用科学记数法表示35000000是（）.

A . 3.5×10⁶ B . 3.5×10⁷ C . 35×10⁶ D . 35×10⁷

答案解析收藏纠错 + 选题
3. (2023·凤岗模拟) 如图是由6个完全相同的小正方体组成的几何体，其俯视图为（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023·绿园模拟) 在数轴上表示数－1和2023的两个点分别为点A和点B，则点A和点B之间的距离为（）个单位．

A . 2022 B . 2023 C . 2024 D . 2025

答案解析收藏纠错 + 选题
5. (2023·绿园模拟) 如图，沿 $\text{[math]}$ 方向修山路，为了加快施工进度，要在小山的另一边同时施工，从 $\text{[math]}$ 上的一点 $\text{[math]}$ 取 $\text{[math]}$ ， $\text{[math]}$ 米， $\text{[math]}$ ，使 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 在一条直线上，那么开挖点 $\text{[math]}$ 与 $\text{[math]}$ 的距离是（）

A . $\text{[math]}$ 米 B . $\text{[math]}$ 米 C . $\text{[math]}$ 米 D . $\text{[math]}$ 米

答案解析收藏纠错 + 选题
6. (2023九上·南浔月考) 如图，点A，B，C，D在⊙O上，AC是⊙O的直径，若∠CAD=25°，则∠ABD的度数为（）

A . 25° B . 50° C . 65° D . 75°

答案解析收藏纠错 + 选题
7. (2023八上·阳谷月考) 观察下列尺规作图的痕迹：

其中，能够说明 $\text{[math]}$ 的是（）

A . ①② B . ②③ C . ①③ D . ③④

答案解析收藏纠错 + 选题
8. (2023·绿园模拟) 如图，四边形OABC是矩形，四边形ADEF是正方形，点A、D在x轴的负半轴上，点C在y轴的正半轴上，点F在AB上，点B、E在反比例函数 $\text{[math]}$ （k为常数，k ≠0）的图象上，正方形ADEF的面积为16，且BF=2AF，则k值为

A . －8 B . －12 C . －24 D . －36

答案解析收藏纠错 + 选题

二、填空题

9. (2023·吉林模拟) 分解因式： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
10. (2023·吉林模拟) 如果关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有两个相等的实数根，那么 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
11. (2024九下·武功模拟) 明代数学家吴敬所著的《九章自述比类大全》中有一首数学诗叫“宝塔装灯”，内容为“远望巍巍塔七层，红灯点点倍加增，共灯三百八十一，请问顶层几盏灯？”大致意思是有一座七层高塔，从底层开始，每层安装的灯的数目都是上一层的2倍，共有381盏灯，请你算出塔的顶层有盏灯．

答案解析收藏纠错 + 选题
12. (2023·绿园模拟) 如图，分别以等边三角形的每个顶点为圆心，以边长为半径，在另两个顶点间画一段圆弧，三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为2，则勒洛三角形的周长为.

答案解析收藏纠错 + 选题
13. (2024九下·广州模拟) 已知一个正多边形的内角和为 $\text{[math]}$ ，则这个正多边形的每个外角为度．

答案解析收藏纠错 + 选题
14. (2023·绿园模拟) 如图，P是抛物线y＝x²-x-4在第四象限的一点，过点P分别向x轴和y轴作垂线，垂足分别为A、B，则四边形OAPB周长的最大值为．

答案解析收藏纠错 + 选题

三、解答题

15. (2023七下·东阿期末) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2023·绿园模拟) 2022卡塔尔世界杯正在激烈进行中，吉祥物“拉伊卜”凭借可爱的造型受到网友喜爱.如图分别是2022年和2018年世界杯的吉祥物和会徽图案，军军制作了4张正面分别印有这四个图案的卡片（卡片的形状、大小、颜色和质地等都相同，这4张卡片分别用字母A，B，C，D表示），并将这4张卡片正面朝下洗匀.
1. （1）军军从中随机抽取1张卡片上的图案是吉祥物“拉伊卜”的概率是；
2. （2）军军从这4张卡片中任意抽取1张卡片，再从剩下的卡片中任意抽取1张卡片，请利用画树状图或列表法，求抽取的2张卡片上的图案都是吉祥物的概率.
答案解析收藏纠错 + 选题
17. (2023·绿园模拟) 为响应“绿色出行”的号召，小张上班由自驾车改为骑自行车．已知小张家距上班地点10千米，他骑自行车平均每小时行驶的路程比他自驾车平均每小时行驶的路程少45千米，他从家出发到上班地点，骑自行车所用的时间是自驾车所用的时间的4倍．小张骑自行车上班平均每小时行驶多少千米？

答案解析收藏纠错 + 选题
18. (2023·绿园模拟) 图①、图②均是由48个小正方形组成的 $\text{[math]}$ 的网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，顶点均在格点的三角形称为格点三角形，如图①， $\text{[math]}$ 即为格点三角形，只用无刻度的直尺，在给定的网格中，按下列要求作图，保留作图痕迹．
1. （1）在图①中作 $\text{[math]}$ ，使 $\text{[math]}$ 是格点三角形且与 $\text{[math]}$ 相似．
2. （2）在图②中作 $\text{[math]}$ ，使 $\text{[math]}$ 与 $\text{[math]}$ 相等，要求点F为格点且不与点C重合．
答案解析收藏纠错 + 选题
19. (2023·绿园模拟) 如图，已知四边形ABCD是平行四边形，点E，F分别是AB，BC上的点，AE=CF，并且∠AED=∠CFD．

求证：
1. （1） △AED≌△CFD；
2. （2）四边形ABCD是菱形．
答案解析收藏纠错 + 选题
20. (2023·绿园模拟) 2023年2月28日，国家统计局发布了《中华人民共和国2022年国民经济和社会发展统计公报》，如图是公报中发布的全国“2018—2022年快递业务量及其增长速度”统计图．
根据以上信息回答下列问题：
1. （1） 2022年，全国快递业务量是亿件，比2021年增长了%．
2. （2） 2018—2022年，全国快递业务量增长速度的中位数是%．
3. （3）根据统计图提供的信息，有下列说法，正确的画“√”，错误的画“×”．
  ①2019年的快递业务量比2018年增加了128.1亿件．（   ）
  ②2021年的快递业务量比2019年增加了4.6%．（   ）
  ③2018—2022年快递业务量逐年增加．（   ）
  ④图中2020—2022年增长速度的折线呈下降趋势，说明2020—2022年快递业务量逐年减少．（   ）
答案解析收藏纠错 + 选题
21. (2024·乌鲁木齐三模) 甲、乙两个工程队分别同时开挖两段河渠，所挖河渠的长度 $\text{[math]}$ 与挖掘时间 $\text{[math]}$ 之间的函数关系如图所示，请根据图象提供的信息解答下列问题：
1. （1）甲队在开挖后6小时内，每小时挖m．
2. （2）当 $\text{[math]}$ 时，求乙队y与x的之间的函数关系式．
3. （3）直接写出开挖后几小时，甲、乙两队挖的河渠的长度相差 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
22. (2023·绿园模拟) 综合与实践课上，老师让同学们以“正方形的折叠”为主题开展数学活动．

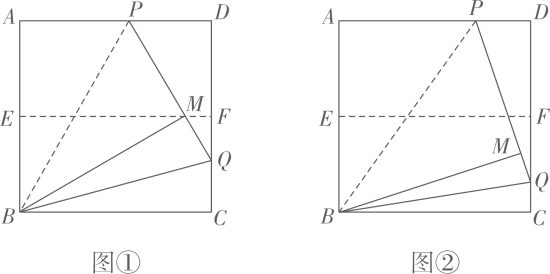
操作：

操作一：对折正方形纸片 $\text{[math]}$ ，使 $\text{[math]}$ 与 $\text{[math]}$ 重合，得到折痕 $\text{[math]}$ ，把纸片展平；

操作二：在 $\text{[math]}$ 上选一点P，沿 $\text{[math]}$ 折叠，使点A落在正方形内部点M处，把纸片展平，连接 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点Q，连接 $\text{[math]}$ ．
1. （1）探究：
  ①如图①，当点M在 $\text{[math]}$ 上时， $\text{[math]}$ ▲ $\text{[math]}$ ．
  ②改变点P在 $\text{[math]}$ 上的位置（点P不与点A、D重合），如图②，判断 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并说明理由．
2. （2）拓展：若正方形纸片 $\text{[math]}$ 的边长为8，当 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
23. (2023·绿园模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，动点P从点A出发，沿AB以每秒3个单位长度的速度向终点B匀速运动．同时，动点Q从点A出发，沿AC以每秒4个单位长度的速度向终点C匀速运动，连接PQ，将 $\text{[math]}$ 绕点P顺时针旋转90°得到 $\text{[math]}$ ，设点P的运动时间为t秒．
1. （1）用含t的代数式表示线段 $\text{[math]}$ 的长度为．
2. （2）当点N落在直线BC上时，求t的值．
3. （3）连接QN，线段QN的中点记为点E，连接PE，当线段PE与 $\text{[math]}$ 的某条边的长度相等时，求t的值．
4. （4）当 $\text{[math]}$ 与 $\text{[math]}$ 重叠部分为四边形时，是否存在一点O，使点O到这个四边形的各个顶点的距离都等于 $\text{[math]}$ ？若存在，直接写出t的值，若不存在，说明理由．
答案解析收藏纠错 + 选题
24. (2023·绿园模拟) 在平面直角坐标系中，过点 $\text{[math]}$ 且平行于x轴的直线与直线 $\text{[math]}$ 交于点P，点P关于直线 $\text{[math]}$ 的对称点为点Q，抛物线 $\text{[math]}$ 经过点P、Q．
1. （1）点P的坐标为；点Q的坐标为．
2. （2）求抛物线 $\text{[math]}$ 的表达式．
3. （3）若点A在抛物线 $\text{[math]}$ 上，且点A横坐标为2m．过点A向直线 $\text{[math]}$ 作垂线，设垂足为B，当点A与点B不重合时，以 $\text{[math]}$ 为边向下作矩形 $\text{[math]}$ ，使 $\text{[math]}$ ．
  ①当矩形 $\text{[math]}$ 的中心恰好落在抛物线 $\text{[math]}$ 上时，求m的值．
  ②当抛物线 $\text{[math]}$ 恰与 $\text{[math]}$ 有交点时，设该交点为E，若 $\text{[math]}$ ，直接写出m的值．
答案解析收藏纠错 + 选题