【浙江衢州】备战2023年中考数学真题变式题第21-22题

• 1. (2022·衢州) 【新知学习】在气象学上，“入夏”由两种平均气温与22℃比较来判断：

  衢州市2021年5月5日~5月14日的两种平均气温统计表 （单位：℃）
  

  注：“五天滑动平均气温”指某一天及其前后各两天的日平均气温的平均数，如：

  (℃)．

  已知2021年的从5月8日起首次连续五天大于或等于22℃，而对应着~ ， 其中第一个大于或等于22℃的是 ， 则5月7日即为我市2021年的“入夏日”．

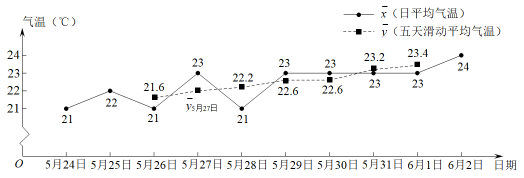
  【新知应用】已知我市2022年的“入夏日”为下图中的某一天，请根据信息解决问题：

  衢州市2022年5月24日~6月2日的两种平均气温折线统计图

  

  1. （1） 求2022年的.
  2. （2） 写出从哪天开始，图中的连续五天都大于或等于22℃．并判断今年的“入夏日”．
  3. （3） 某媒体报道：“夏天姗姗来迟，衢州2022年的春天比去年长．”你认为这样的说法正确吗？为什么？（我市2021年和2022年的入春时间分别是2月1日和2月27日）

  答案解析 收藏 纠错 + 选题

• 2. (2017·嘉兴)

  小明为了了解气温对用电量的影响，对去年自己家的每月用电量和当地气温进行了统计．当地去年每月的平均气温如图1，小明家去年月用电量如图2．
  

  根据统计表，回答问题：

  

  1. （1） 当地去年月平均气温的最高值、最低值各为多少？相应月份的用电量各是多少？

  2. （2） 请简单描述月用电量与气温之间的关系；

  3. （3） 假设去年小明家用电量是所在社区家庭年用电量的中位数，据此他能否预测今年该社区的年用电量？请简要说明理由．

  答案解析 收藏 纠错 + 选题
• 3.

  王大伯几年前承包了甲、乙两片荒山，各栽100棵杨梅树，成活98%．现已挂果，经济效益初步显现，为了分析收成情况，他分别从两山上随意各采摘了4棵树上的杨梅，每棵的产量如折线统计图所示．

  （1）分别计算甲、乙两山样本的平均数，并估算出甲、乙两山杨梅的产量总和；

  （2）试通过计算说明，哪个山上的杨梅产量较稳定？

  
  

  答案解析 收藏 纠错 + 选题
• 4. (2023九下·靖江期中) 某农业科技部门为了解甲、乙两种新品西瓜的品质（大小、甜度等），进行了抽样调查.在相同条件下，随机抽取了两种西瓜各7份样品，对西瓜的品质进行评分（百分制），并对数据进行收集、整理，下面给出两种西瓜得分的统计图表.

  甲、乙两种西瓜得分表

  序号	1	2	3	4	5	6	7
  甲种西瓜（分）	75	85	86	88	90	96	96
  乙种西瓜（分）	80	83	87	90	90	92	94

  

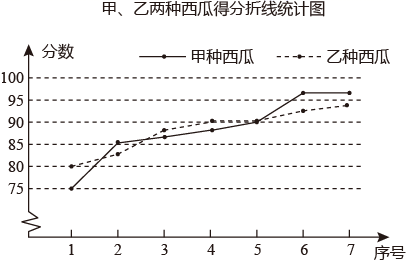
  甲、乙两种西瓜得分统计表

  	平均数	中位数	众数
  甲种西瓜	88	a	96
  乙种西瓜	88	90	b

  1. （1） ， ；
  2. （2） 从方差的角度看，种西瓜的得分较稳定（填“甲”或“乙”）；
  3. （3） 小明认为甲种西瓜的品质较好些，小军认为乙种西瓜的品质较好些.请结合统计图表中的信息分别写出他们的理由.

  答案解析 收藏 纠错 + 选题
• 5. (2021·桂林) 某班为了从甲、乙两名同学中选出一名同学代表班级参加学校的投篮比赛，对甲、乙两人进行了5次投篮试投比赛，试投每人每次投球10个.两人5次试投的成绩统计图如图所示.

  

  1. （1） 甲同学5次试投进球个数的众数是多少？
  2. （2） 求乙同学5次试投进球个数的平均数；
  3. （3） 不需计算，请根据折线统计图判断甲、乙两名同学谁的投篮成绩更加稳定？
  4. （4） 学校投篮比赛的规则是每人投球10个，记录投进球的个数.由往届投篮比赛的结果推测，投进8个球即可获奖，但要取得冠军需要投进10个球.请你根据以上信息，从甲、乙两名同学中推荐一名同学参加学校的投篮比赛，并说明推荐的理由.

  答案解析 收藏 纠错 + 选题

• 6. (2017·湖州)

  为积极创建全国文明城市，某市对某路口的行人交通违章情况进行了 天的调查，将所得数据绘制成如下统计图（图2不完整）：

  

  请根据所给信息，解答下列问题：

  1. （1） 第 天，这一路口的行人交通违章次数是多少次？这 天中，行人交通违章 次的有多少天？

  2. （2） 请把图2中的频数直方图补充完整；

  3. （3） 通过宣传教育后，行人的交通违章次数明显减少．经对这一路口的再次调查发现，平均每天的行人交通违章次数比第一次调查时减少了 次，求通过宣传教育后，这一路口平均每天还出现多少次行人的交通违章？

  答案解析 收藏 纠错 + 选题
• 7. (2021·徐州) 某市近年参加初中学业水平考试的人数（以下简称“中考人数”）的情况如图所示.

  

  根据图中信息，解决下列问题：

  1. （1） 这11年间，该市中考人数的中位数是万人；
  2. （2） 与上年相比，该市中考人数增加最多的年份是年；
  3. （3） 下列选项中，与该市2022年中考人数最有可能接近的是（   ）

     A . 12.8万人 ； B . 14.0万人； C . 15.3万人
  4. （4） 2019年上半年，该市七、八、九三个年级的学生总数约为（   ）

     A . 23.1万人； B . 28.1万人； C . 34.4万人
  5. （5） 该市2019年上半年七、八、九三个年级的数学教师共有4000人，若保持数学教师与学生的人数之比不变，根据（3）（4）的结论，该市2020年上半年七、八、九三个年级的数学教师较上年同期增加多少人（结果取整数）？

  答案解析 收藏 纠错 + 选题
• 8. (2021九上·新乐期末) 近5年，我省家电业的发展发生了新变化.以甲、乙、丙3种家电为例，将这3种家电2016～2020年的产量（单位：万台）绘制成如图所示的折线统计图，图中只标注了甲种家电产量的数据.

  

  观察统计图回答下列问题：

  1. （1） 这5年甲种家电产量的中位数为 万台；
  2. （2） 若将这5年家电产量按年份绘制成5个扇形统计图，每个统计图只反映该年这3种家电产量占比，其中有一个扇形统计图的某种家电产量占比对应的圆心角大于180°，这个扇形统计图对应的年份是 年；
  3. （3） 小明认为：某种家电产量的方差越小，说明该家电发展趋势越好.你同意他的观点吗？请结合图中乙、丙两种家电产量变化情况说明理由.

  答案解析 收藏 纠错 + 选题
• 9. (2021·贺州) 如图，某大学农学院的学生为了解试验田杂交水稻秧苗的长势，从中随机抽取样本对苗高进行了测量，根据统计结果（数据四舍五入取整），绘制统计图.

  

  1. （1） 本次抽取的样本水稻秧苗为株；
  2. （2） 求出样本中苗高为 的秧苗的株数，并完成折线统计图；
  3. （3） 根据统计数据，若苗高大于或等于 视为优良秧苗，请你估算该试验田90000株水稻秧苗中达到优良等级的株数.

  答案解析 收藏 纠错 + 选题
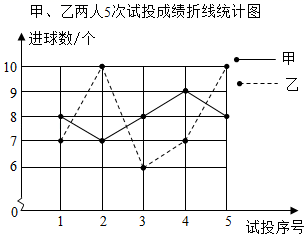
• 10. (2024·恩施模拟) 九（1）班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛，在相同的条件下，分别对两名男生进行了八次一分钟跳绳测试.现将测试结果绘制成如下不完整的统计图表，请根据统计图表中的信息解答下列问题：

  	平均数	中位数	众数	方差
  甲	175			93.75
  乙	175	175	180，175，170

  

  1. （1） 求 、 的值；
  2. （2） 若九（1）班选一位成绩稳定的选手参赛，你认为应选谁，请说明理由；
  3. （3） 根据以上的数据分析，请你运用所学统计知识，任选两个角度评价甲乙两名男生一分钟跳绳成绩谁优.

  答案解析 收藏 纠错 + 选题

• 11. (2022·宁夏) 宁夏某枸杞育种改良试验基地对新培育的甲、乙两个品种各试种一亩，从两块试验地中各随机抽取10棵，对其产量（千克/棵）进行整理分析．下面给出了部分信息：

  甲品种：2.0，3.2，3.1，3.2，3.1，2.5，3.2，3.6，3.8，3.9

  乙品种：如图所示
  

  	平均数	中位数	众数	方差
  甲品种	3.16		3.2	0.29
  乙品种	3.16	3.3		0.15

  
  根据以上信息，完成下列问题：

   

  1. （1） 填空：，；
  2. （2） 若乙品种种植棵，估计其产量不低于千克的棵数；
  3. （3） 请从某一个方面简要说明哪个品种更好．

  答案解析 收藏 纠错 + 选题

• 12. (2022·衢州) 金师傅近期准备换车，看中了价格相同的两款国产车．

  

  1. （1） 用含a的代数式表示新能源车的每千米行驶费用．
  2. （2） 若燃油车的每千米行驶费用比新能源车多0.54元．

     ①分别求出这两款车的每千米行驶费用．

     ②若燃油车和新能源车每年的其它费用分别为4800元和7500元．问：每年行驶里程为多少千米时，买新能源车的年费用更低？（年费用=年行驶费用+年其它费用）

  答案解析 收藏 纠错 + 选题

• 13. (2023·怀化模拟) 某班在庆祝中国共产主义青年团成立100周年活动中，给学生发放笔记本和钢笔作为纪念品．已知每本笔记本比每支钢笔多2元，用240元购买的笔记本数量与用200元购买的钢笔数量相同．

  1. （1） 笔记本和钢笔的单价各多少元？
  2. （2） 若给全班50名学生每人发放一本笔记本或一支钢笔作为本次活动的纪念品，要使购买纪念品的总费用不超过540元，最多可以购买多少本笔记本？

  答案解析 收藏 纠错 + 选题
• 14. (2022九上·博白月考) 某校购进一批篮球和排球，篮球的单价比排球的单价多30元．已知330元购进的篮球数量和240元购进的排球数量相等．

  1. （1） 篮球和排球的单价各是多少元？
  2. （2） 现要购买篮球和排球共20个，总费用不超过1800元．篮球最多购买多少个？

  答案解析 收藏 纠错 + 选题
• 15. (2022·安顺) 阅读材料：被誉为“世界杂交水稻之父”的“共和国勋章”获得者袁隆平，成功研发出杂交水稻，杂交水稻的亩产量是普通水稻的亩产量的2倍．现有两块试验田，块种植杂交水稻，块种植普通水稻，块试验田比块试验田少4亩．

  1. （1） 块试验田收获水稻9600千克、块试验田收获水稻7200千克，求普通水稻和杂交水稻的亩产量各是多少千克？
  2. （2） 为了增加产量，明年计划将种植普通水稻的块试验田的一部分改种杂交水稻，使总产量不低于17700千克，那么至少把多少亩块试验田改种杂交水稻？

  答案解析 收藏 纠错 + 选题
• 16. (2022·丹东) 为推动家乡学校篮球运动的发展，某公司计划出资12000元购买一批篮球赠送给家乡的学校．实际购买时，每个篮球的价格比原价降低了20元，结果该公司出资10000元就购买了和原计划一样多的篮球，每个篮球的原价是多少元？

  答案解析 收藏 纠错 + 选题

• 17. (2022·益阳) 在某市组织的农机推广活动中，甲、乙两人分别操控A、B两种型号的收割机参加水稻收割比赛．已知乙每小时收割的亩数比甲少40%，两人各收割6亩水稻，乙则比甲多用0.4小时完成任务；甲、乙在收割过程中对应收稻谷有一定的遗落或破损，损失率分别为3%，2%．

  1. （1） 甲、乙两人操控A、B型号收割机每小时各能收割多少亩水稻？
  2. （2） 某水稻种植大户有与比赛中规格相同的100亩待收水稻，邀请甲、乙两人操控原收割机一同前去完成收割任务，要求平均损失率不超过2.4%，则最多安排甲收割多少小时？

  答案解析 收藏 纠错 + 选题
• 18. (2022九上·岳麓开学考) 某超市采购了两批同样的冰墩墩挂件，第一批花了6600元，第二批花了8000元，第一批每个挂件的进价是第二批的1.1倍，且第二批比第一批多购进50个．

  1. （1） 求第二批每个挂件的进价；
  2. （2） 两批挂件售完后，该超市以第二批每个挂件的进价又采购一批同样的挂件，经市场调查发现，当售价为每个60元时，每周能卖出40个，若每降价1元，每周多卖10个，由于货源紧缺，每周最多能卖90个，求每个挂件售价定为多少元时，每周可获得最大利润，最大利润是多少？

  答案解析 收藏 纠错 + 选题
• 19. (2023·汨罗一模) 某健身器材店计划购买一批篮球和排球，已知每个篮球进价是每个排球进价的1.5倍，若用3600元购进篮球的数量比用3200元购进排球的数量少10个．

  1. （1） 篮球、排球的进价分别为每个多少元?
  2. （2） 该健身器材店决定用不多于28000元购进篮球和排球共300个进行销售，最多可以购买多少个篮球?

  答案解析 收藏 纠错 + 选题

• 20. (2021·江西) 甲，乙两人去市场采购相同价格的同一种商品，甲用2400元购买的商品数量比乙用3000元购买的商品数量少10件．

  1. （1） 求这种商品的单价；
  2. （2） 甲，乙两人第二次再去采购该商品时，单价比上次少了20元/件，甲购买商品的总价与上次相同，乙购买商品的数量与上次相同，则甲两次购买这种商品的平均单价是元/件，乙两次购买这种商品的平均单价是元/件．
  3. （3） 生活中，无论油价如何变化，有人总按相同金额加油，有人总按相同油量加油，结合（2）的计算结果，建议按相同加油更合算（填“金额”或“油量”）．

  答案解析 收藏 纠错 + 选题