浙江省2023年中考数学真题分类汇编05 二次函数

更新时间：2023-07-10 浏览次数：75 类型：二轮复习

一、选择题

1. 已知点 $\text{[math]}$ 在同一个函数图象上，则这个函数图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024九上·上海市月考) 抛物线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点，若 $\text{[math]}$ ，则直线 $\text{[math]}$ 一定经过（）．

A . 第一、二象限 B . 第二、三象限 C . 第三、四象限 D . 第一、四象限

答案解析收藏纠错 + 选题
3. (2024九下·临渭模拟) 设二次函数 $\text{[math]}$ 是实数 $\text{[math]}$ ，则（）

A . 当 $\text{[math]}$ 时，函数 $\text{[math]}$ 的最小值为 $\text{[math]}$ B . 当 $\text{[math]}$ 时，函数 $\text{[math]}$ 的最小值为 $\text{[math]}$ C . 当 $\text{[math]}$ 时，函数 $\text{[math]}$ 的最小值为 $\text{[math]}$ D . 当 $\text{[math]}$ 时，函数 $\text{[math]}$ 的最小值为 $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九下·济宁模拟) 已知二次函数 $\text{[math]}$ ，下列说法正确的是（）

A . 点 $\text{[math]}$ 在该函数的图象上 B . 当 $\text{[math]}$ 且 $\text{[math]}$ 时， $\text{[math]}$ C . 该函数的图象与x轴一定有交点 D . 当 $\text{[math]}$ 时，该函数图象的对称轴一定在直线 $\text{[math]}$ 的左侧

答案解析收藏纠错 + 选题
5. (2023九上·上虞月考) 一个球从地面竖直向上弹起时的速度为10米/秒，经过t(秒)时球距离地面的高度h(米)适用公式h=10t-5t² ，那么球弹起后又回到地面所花的时间t(秒)是（）

A . 5 B . 10 C . 1 D . 2

答案解析收藏纠错 + 选题

二、填空题

6. (2023·绍兴) 在平面直角坐标系 $\text{[math]}$ 中，一个图形上的点都在一边平行于 $\text{[math]}$ 轴的矩形内部（包括边界），这些矩形中面积最小的矩形称为该图形的关联矩形.例如：如图，函数 $\text{[math]}$ $\text{[math]}$ 的图象（抛物线中的实线部分），它的关联矩形为矩形 $\text{[math]}$ .若二次函数 $\text{[math]}$ 图象的关联矩形恰好也是矩形 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题

三、解答题

7. (2023·杭州) 设二次函数 $\text{[math]}$ ，（ $\text{[math]}$ ， $\text{[math]}$ 是实数）．已知函数值 $\text{[math]}$ 和自变量 $\text{[math]}$ 的部分对应取值如下表所示：

$\text{[math]}$	…	$\text{[math]}$	0	1	2	3	…
$\text{[math]}$	…	$\text{[math]}$	1	$\text{[math]}$	1	$\text{[math]}$	…

（1）若 $\text{[math]}$ ，求二次函数的表达式；
（2）写出一个符合条件的 $\text{[math]}$ 的取值范围，使得 $\text{[math]}$ 随 $\text{[math]}$ 的增大而减小．
（3）若在m、n、p这三个实数中，只有一个是正数，求 $\text{[math]}$ 的取值范围．

答案解析收藏纠错 + 选题

8. (2023九上·怀远期中) 如图，已知二次函数 $\text{[math]}$ 图象经过点 $\text{[math]}$ 和 $\text{[math]}$ ．
1. （1）求该二次函数的表达式及图象的顶点坐标．
2. （2）当 $\text{[math]}$ 时，请根据图象直接写出x的取值范围．
答案解析收藏纠错 + 选题
9. (2023九上·滨江月考) 已知二次函数 $\text{[math]}$ .
1. （1）当 $\text{[math]}$ 时，
  ①求该函数图象的顶点坐标.
  ②当 $\text{[math]}$ 时，求 $\text{[math]}$ 的取值范围.
2. （2）当 $\text{[math]}$ 时， $\text{[math]}$ 的最大值为2；当 $\text{[math]}$ 时， $\text{[math]}$ 的最大值为3，求二次函数的表达式.
答案解析收藏纠错 + 选题
10. (2023·舟山) 在二次函数 $\text{[math]}$ 中，
1. （1）若它的图象过点 $\text{[math]}$ ，则t的值为多少？
2. （2）当 $\text{[math]}$ 时，y的最小值为 $\text{[math]}$ ，求出t的值：
3. （3）如果 $\text{[math]}$ 都在这个二次函数的图象上，且 $\text{[math]}$ ，求m的取值范围。
答案解析收藏纠错 + 选题
11. 已知点(-m，0)和(3m，0)在二次函数y=ax²+bx+3(a，b是常数，a≠0)的图象上。
1. （1）当m=-1时，求a和b的值：
2. （2）若二次函数的图象经过点A(n，3)且点A不在坐标轴上，当-2<m<-1时，求n的取值范围：
3. （3）求证：b²+4a=0．
答案解析收藏纠错 + 选题
12. (2024·长沙模拟) 一次足球训练中，小明从球门正前方8m的 $\text{[math]}$ 处射门，球射向球门的路线呈抛物线.当球飞行的水平距离为6m时，球达到最高点，此时球离地面3m.已知球门高OB为2.44m，现以 $\text{[math]}$ 为原点建立如图所示直角坐标系.
1. （1）求抛物线的函数表达式，并通过计算判断球能否射进球门（忽略其他因素）。
2. （2）对本次训练进行分析，若射门路线的形状、最大高度均保持不变，则当时他应该带球向正后方移动多少米射门，才能让足球经过点 $\text{[math]}$ 正上方2.25m处?
答案解析收藏纠错 + 选题

13. (2023·台州) 【问题背景】

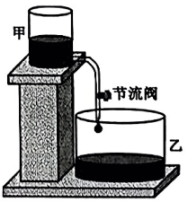
“刻漏”是我国古代的一种利用水流计时的工具．综合实践小组准备用甲、乙两个透明的竖直放置的容器和一根带节流阀（控制水的流速大小）的软管制作简易计时装置．

【实验操作】

综合实践小组设计了如下的实验：先在甲容器里加满水，此时水面高度为30cm，开始放水后每隔10min观察一次甲容器中的水面高度，获得的数据如下表：

流水时间t/min	0	10	20	30	40
水面高度h/cm（观察值）	30	29	28.1	27	25.8

任务1 分别计算表中每隔10min水面高度观察值的变化量．

【建立模型】

小组讨论发现：“ $\text{[math]}$ ， $\text{[math]}$ ”是初始状态下的准确数据，水面高度值的变化不均匀，但可以用一次函数近似地刻画水面高度h与流水时间t的关系．

任务2 利用 $\text{[math]}$ 时， $\text{[math]}$ ； $\text{[math]}$ 时， $\text{[math]}$ 这两组数据求水面高度h与流水时间t的函数解析式．

【反思优化】

经检验，发现有两组表中观察值不满足任务2中求出的函数解析式，存在偏差．小组决定优化函数解析式，减少偏差．通过查阅资料后知道：t为表中数据时，根据解析式求出所对应的函数值，计算这些函数值与对应h的观察值之差的平方和，记为w；w越小，偏差越小．

任务3 ⑴计算任务2得到的函数解析式的w值．

⑵请确定经过 $\text{[math]}$ 的一次函数解析式，使得w的值最小．

【设计刻度】

得到优化的函数解析式后，综合实践小组决定在甲容器外壁设计刻度，通过刻度直接读取时间．

任务4 请你简要写出时间刻度的设计方案．

答案解析收藏纠错 + 选题

14. (2023·金华) 如图，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴， $\text{[math]}$ 轴分别交于点A，B，抛物线的顶点 $\text{[math]}$ 在直线AB上，与 $\text{[math]}$ 轴的交点为C，D，其中点 $\text{[math]}$ 的坐标为 $\text{[math]}$ .直线BC与直线PD相交于点 $\text{[math]}$ .
1. （1）如图2，若抛物线经过原点 $\text{[math]}$ .
  ①求该抛物线的函数表达式；②求 $\text{[math]}$ 的值.
2. （2）连结 $\text{[math]}$ 与 $\text{[math]}$ 能否相等？若能，求符合条件的点 $\text{[math]}$ 的横坐标；若不能，试说明理由.
答案解析收藏纠错 + 选题