
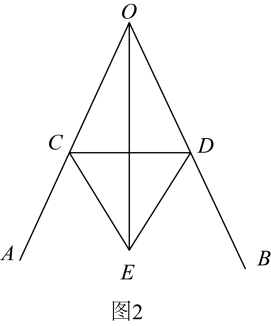
若和
都是等腰直角三角形,且
, 如图②:若
和
都是等腰三角形,且
, 如图③:其他条件不变,判断
和
之间的数量关系,写出你的猜想,并利用图②或图③进行证明.


请写出平分
的依据:;

小明根据以上信息研究发现:不一定必须是等边三角形,只需
即可.他查阅资料:我国古代已经用角尺平分任意角.做法如下:如图3,在
的边
,
上分别取
, 移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线
是
的平分线,请说明此做法的理由;

小明将研究应用于实践.如图4,校园的两条小路和
, 汇聚形成了一个岔路口A,现在学校要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等.试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置.(保留作图痕迹,不写作法)
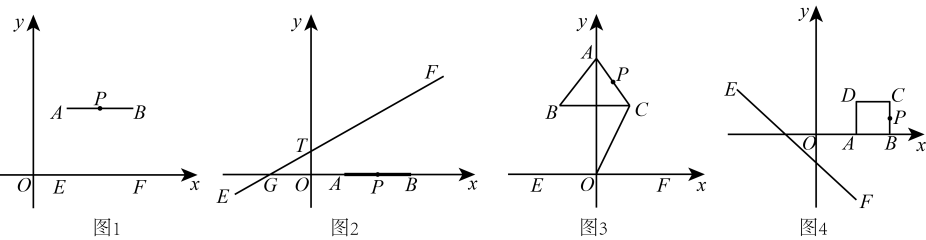
例如:如图1,已知点 ,
,
在线段
上,则点
是直线
:
轴的“伴随点”.
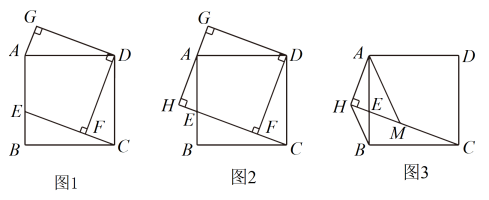
数学活动课上,老师出示了一个问题:如图1,在矩形ABCD中,E是边上一点,
于点F,
,
,
. 试猜想四边形
的形状,并说明理由;
小睿受此问题启发,逆向思考并提出新的问题:如图2,在正方形中,E是边
上一点,
于点F,
于点H,
交
于点G,可以用等式表示线段
,
,
的数量关系,请你思考并解答这个问题;
小博深入研究小睿提出的这个问题,发现并提出新的探究点:如图3,在正方形中,E是边
上一点,
于点H,点M在
上,且
, 连接
,
, 可以用等式表示线段
,
的数量关系,请你思考并解答这个问题.