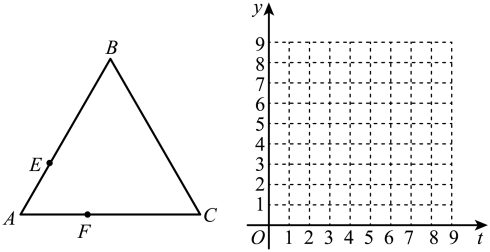
用直尺和圆规,作的垂直平分线交
于点E,交
于点F,垂足为点O.(只保留作图痕迹)
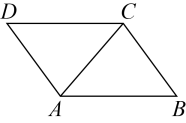
已知:如图,四边形是平行四边形,
是对角线,
垂直平分
, 垂足为点O.
求证: .
证明:∵四边形是平行四边形,
∴ .
∴ ▲ .
∵垂直平分
,
∴ ▲ .
又 ▲ .
∴ .
∴ .
小虹再进一步研究发现,过平行四边形对角线中点的直线与平行四边形一组对边相交形成的线段均有此特征.请你依照题意完成下面命题:
过平行四边形对角线中点的直线 ▲ .