2023年浙教版数学九年级上册3.3 垂径定理同步测试（培...

更新时间：2023-08-01 浏览次数：78 类型：同步测试

一、选择题

1. (2022九上·丰城开学考) 如图，AB 为⊙O 的直径，点 D 是弧 AC 的中点，过点 D 作 DE⊥AB 于点 E，延长 DE 交⊙O 于点 F，若 AC＝12，AE＝3，则⊙O 的直径长为（）

A . 7.5 B . 15 C . 16 D . 18

答案解析收藏纠错 + 选题
2. (2023九上·诸暨月考) $\text{[math]}$ 是以半径为 $\text{[math]}$ 的圆的圆周上的两点， $\text{[math]}$ 为 $\text{[math]}$ 的中点，以线段 $\text{[math]}$ 为邻边作菱形 $\text{[math]}$ ，顶点 $\text{[math]}$ 恰好为该圆直径的三等分点，则该菱形的边长为（）．

A . $\text{[math]}$ 或 $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022九上·嘉兴期中) 如图，C是以AB为直径的半圆O上一点，连接AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG．DE，FG， $\text{[math]}$ ， $\text{[math]}$ 的中点分别是M，N，P，Q．若MP+NQ＝14，AC+BC＝18，则AB的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 13 D . 16

答案解析收藏纠错 + 选题
4. (2022九上·金东月考) 如图，在⊙O中，弦AB∥CD，OP⊥CD，OM＝MN，AB＝18，CD＝12，则⊙O的半径为（）

A . 4 B . 4 $\text{[math]}$ C . 4 $\text{[math]}$ D . 4 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022九上·定海月考) 如图，在平面直角坐标系中，点A，C，N的坐标分别为（-2，0），（2，0），（4，3），以点C为圆心，2为半径画⊙C，点P在⊙C上运动，连接AP，交⊙C于点Q，点M为线段QP的中点，连接MN，则线段MN的最小值为（）

A . $\text{[math]}$ B . 3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021九上·泗水期中) 如图，在等腰△ABC中，AB＝AC＝4 $\text{[math]}$ ， BC＝16，按下列步骤作图：①以点A为圆心，适当的长度为半径作弧，分别交AB，AC于点E，F，再分别以点E，F为圆心，大于 $\text{[math]}$ EF的长为半径作弧相交于点H，作射线AH；②分别以点A，B为圆心，大于 $\text{[math]}$ AB的长为半径作弧相交于点M，N，作直线MN，交射线AH于点O；③以点O为圆心，线段OA长为半径作圆．则⊙O的半径为（）

A . 4 $\text{[math]}$ B . 10 C . 5 D . 4

答案解析收藏纠错 + 选题
7. (2023九上·姑苏月考) 如图，在等边 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，动点 $\text{[math]}$ 分别在 $\text{[math]}$ 上，且 $\text{[math]}$ ，作 $\text{[math]}$ 的外接圆 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ .当动点 $\text{[math]}$ 从点 $\text{[math]}$ 向点 $\text{[math]}$ 运动时，线段 $\text{[math]}$ 长度的变化情况为（）

A . 一直不变 B . 一直变大 C . 先变小再变大 D . 先变大再变小

答案解析收藏纠错 + 选题
8. (2022九上·温州月考) 如图，已知点C是线段AB的中点，CD⊥AB且CD＝ $\text{[math]}$ AB＝a，延长CB至E，使得BE＝b，以CD，CE为边作矩形CEFD，连接并延长DB，交FE的延长线于点G，连接AG，《几何原本》中利用该图解释了代数式（2a+b）²+b²＝2[（a+b）²+a²]的几何意义，以AG为直径作圆，交AF于点H，若a＝9，b＝6，则HG的长为（）

A . 5 $\text{[math]}$ B . 18 C . 3 $\text{[math]}$ D . 17

答案解析收藏纠错 + 选题
9. (2022九上·桐庐期中) 如图，AB为⊙O的直径，点C为⊙O上一点，连接CO，作AD $\text{[math]}$ OC，若CO＝ $\text{[math]}$ ，AC＝2，则AD＝（　　）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2020九下·广陵月考) 如图，AB为⊙O的直径，C为⊙O上一点，其中AB＝4，∠AOC＝120°，P为⊙O上的动点，连AP，取AP中点Q，连CQ，则线段CQ的最大值为（）

A . 3 B . 1+ $\text{[math]}$ C . 1+3 $\text{[math]}$ D . 1+ $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2022九上·哈尔滨月考) 如图， $\text{[math]}$ 的直径 $\text{[math]}$ ， CD是 $\text{[math]}$ 的弦， $\text{[math]}$ 垂足为P，连接AC、AD， $\text{[math]}$ 是等边三角形，则CD的长为．

答案解析收藏纠错 + 选题
12. (2022九上·舟山月考) 一根排水管的截面如图所示，已知排水管的半径OB＝10，水面宽AB＝12，如果再注入一些水，当水面AB的宽变为16时，则水面AB上升的高度为。

答案解析收藏纠错 + 选题
13. (2021九上·大石桥期末) 在△ABC中，∠BAC=60°，∠ABC=45°，AB=2，D是线段BC上的一个动点，以AD为直径画⊙O 分别交AB、AC于E、F，连接EF，则线段EF长度的最小值是．

答案解析收藏纠错 + 选题
14. (2020九上·嘉兴期中) 如图，C、D是以AB为直径的圆O上的两个动点（点C、D不与A、B重合），在运动过程中弦CD始终保持不变，M是弦CD的中点，过点C作CP⊥AB于点P．若CD=3，AB=5，PM最大值是．

答案解析收藏纠错 + 选题
15. (2019九上·温州月考) 如图，在△ABC中，AC=BC=5，AB=6，点D为AC上一点，作DE∥AB交BC于点E，点C关于DE的对称点为点O，以OA为半径作⊙O恰好经过点C，并交直线DE于点M，N，则MN的值为。

答案解析收藏纠错 + 选题

三、解答题

16. (2022九上·柯城月考) 根据以下素材，探索完成任务.

如何确定隧道的限高？
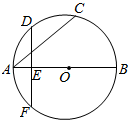
素材1	从小清家到附近山区的一条双行线公路上有一个隧道，在隧道口有一个限高标志（如图1），表示禁止装载高度（车顶最高处到地面）超过 $\text{[math]}$ 的车辆通行.那么这个限高 $\text{[math]}$ 是如何确定的呢？
素材2	小清通过实地调查和查阅相关资料，获得以下信息： ①隧道的横截面成轴对称，由一个矩形和一个弓形构成. ②隧道内的总宽度为 $\text{[math]}$ ，双行车道宽度为 $\text{[math]}$ ，隧道圆拱内壁最高处距路面 $\text{[math]}$ ，矩形的高为 $\text{[math]}$ ，车道两侧的人行道宽 $\text{[math]}$ . ③为了保证安全，交通部门要求行驶车辆的顶部（设为平顶）与隧道圆拱内壁在竖直方向上的高度差相差最少 $\text{[math]}$ .
问题解决
任务1	计算半径	求图1中弓形所在圆的半径.
任务2	确定限高	如图2，在安全的条件下， $\text{[math]}$ 的限高是如何确定的？请通过计算说明理由.（参考数据： $\text{[math]}$ ，结果保留一位小数）
任务3	尝试设计	如果要使高度不超过 $\text{[math]}$ ，宽为 $\text{[math]}$ 的货车能顺利通过这个隧道，且不改变隧道内的总宽度（ $\text{[math]}$ ）和矩形的高（ $\text{[math]}$ ），如何设计隧道的弓形部分（求弓形所在圆的半径至少为多少米？）（参考数据： $\text{[math]}$ ，结果保留一位小数）

答案解析收藏纠错 + 选题

17. (2022九上·龙港期中) 根据以下素材，探索完成任务.

如何设计高架桥的限高及车道宽方案？
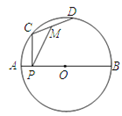
素材1	图1高架桥是一段圆弧拱形结构，图2是它的示意图.经测量，拱形跨度24m，拱顶离地面6m.
素材2	如图3，某道路规划部门计划将左侧公路分为非机动车道、机动车道一、机动车道二及绿化带四部分，原计划设计非机动车道宽3m，每条机动车道宽均3.5m.为了保证车辆的行驶安全，高架下方需要设置限高标志以警示车辆驾驶员.（限高即图中FC的高度）
素材3	如图4，由于城市道路绿化需求，道路规划部门确定新方案为在非机动车道和机动车道一之间增加一条宽为1m的绿化带，中间绿化带宽度不变，每条机动车道道宽均不小于3.25m且相等，非机动车道最高高度不小于2.5m.
	问题解决
任务1	确定桥拱所在圆弧的半径.	在图2中补好图形，标注字母、数据等信息，求出桥拱所在圆弧的半径长.
任务2	探究原计划该高架桥下方机动车道一的限高要求.	在图3中画出图形，标注字母、数据等信息，计算确定机动车道一的限高高度.
任务3	拟定新方案下非机动车道和机动车车道宽度.	给出一对符合新方案要求的非机动车道和机动车道的道宽值. （参考数值： $\text{[math]}$ ＝9.63， $\text{[math]}$ ＝11.61）

答案解析收藏纠错 + 选题

四、综合题

18. (2022九上·盐城期末) 【概念提出】圆心到弦的距离叫做该弦的弦心距．
【数学理解】如图①，在 $\text{[math]}$ 中，AB是弦， $\text{[math]}$ ，垂足为P，则OP的长是弦AB的弦心距．
1. （1）若 $\text{[math]}$ 的半径为5，OP的长为3，则AB的长为．
2. （2）若 $\text{[math]}$ 的半径确定，下列关于AB的长随着OP的长的变化而变化的结论：
  ①AB的长随着OP的长的增大而增大；②AB的长随着OP的长的增大而减小；③AB的长与OP的长无关．
  其中所有正确结论的序号是．
3. （3）【问题解决】若弦心距等于该弦长的一半，则这条弦所对的圆心角的度数为°．
4. （4）已知如图②给定的线段EF和 $\text{[math]}$ ，点Q是 $\text{[math]}$ 内一定点．过点Q作弦AB，满足 $\text{[math]}$ ，请问这样的弦可以作条．
答案解析收藏纠错 + 选题
19. (2021九上·三台期中) 如图，在半径为2的扇形OAB中， $\text{[math]}$ ，点C是 $\text{[math]}$ 上的一个动点（不与点A，B重合）， $\text{[math]}$ ， $\text{[math]}$ ，垂足分别为D，E．
1. （1）当 $\text{[math]}$ 时，求线段OD的长；
2. （2）在 $\text{[math]}$ 中，是否存在长度保持不变的边？如果存在，请指出并求其长度；如果不存在，请说明理由．
3. （3）在 $\text{[math]}$ 中，是否存在度数保持不变的角？如果存在，请指出并求其度数；如果不存在，请说明理由．
答案解析收藏纠错 + 选题