2023年浙教版数学七年级上册3.2 实数同步测试（培优版...

更新时间：2023-08-07 浏览次数：67 类型：同步测试

一、选择题（每题3分，共30分）

1. (2019七下·柳州期末) 下列四个式子：
① $\text{[math]}$ ；② $\text{[math]}$ ＜8；③ $\text{[math]}$ ＜1；④ $\text{[math]}$ ＞0.5．

其中大小关系正确的式子的个数是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
2. (2023·朝阳模拟) 实数a ， b ， c在数轴上的对应点的位置如图所示．下列式子正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022七下·潮安期末) 若m＝5n（m、n是正整数），且 $\text{[math]}$ ，则与实数 $\text{[math]}$ 的最大值最接近的数是（）

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
4. (2024七下·江陵期中) 根据表中的信息判断，下列语句正确的是（）
n
256
259.21
262.44
265.69
268.96
272.25
275.56
$\text{[math]}$
16
16.1
16.2
16.3
16.4
16.5
16.6

A . $\text{[math]}$ B . $\text{[math]}$ C . 只有3个正整数n满足 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021七上·腾冲期末) 如图，A、B两点在数轴上表示的数分别为a、b，以下结论：①a﹣b＞0；②a+b＜0；③（b﹣1）（a+1）＞0；④ $\text{[math]}$ ．其中结论正确的是（）

A . ①② B . ③④ C . ①③ D . ①②④

答案解析收藏纠错 + 选题
6. (2023七下·下城期中) 设681×2019﹣681×2018=a ， 2015×2016﹣2013×2018=b ， $\text{[math]}$ ，则a ， b ， c的大小关系是（）

A . b＜c＜a B . a＜c＜b C . b＜a＜c D . c＜b＜a

答案解析收藏纠错 + 选题
7. (2020七上·镇海期中) 数轴上A，B，C三点所代表的数分别是a、b、2，且 $\text{[math]}$ .下列四个选项中，有（）个能表示A，B，C三点在数轴上的位置关系.
① ② ③ ④

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
8. (2019七上·吴兴期中) 实数a，b，c，d在数轴上的对应点的位置如图所示，则正确的结论是（）

A . a>–4 B . bd>0 C . |a|>|d| D . b+c>0

答案解析收藏纠错 + 选题
9. (2019七下·天台期末) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 表示取三个数中最小的那个数﹒例如：当 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ = $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ =3﹒当 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ = $\text{[math]}$ 时，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2019七下·潜江月考) 对于实数x，我们规定[x]表示不大于x的最大整数，如[4]=4，[ $\text{[math]}$ ]=1，[﹣2.5]=﹣3.现对82进行如下操作：82 $\text{[math]}$ [ $\text{[math]}$ ]=9 $\text{[math]}$ [ $\text{[math]}$ ]=3 $\text{[math]}$ [ $\text{[math]}$ ]=1，这样对82只需进行3次操作后变为1，类似地，对121只需进行多少次操作后变为1（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题（每空4分，共20分）

11. (2023七下·闽清期末) 如图，把半径为1的圆从数轴上表示-1的点A开始沿数轴向右滚动一周，圆上的点A到达点 $\text{[math]}$ ，则点 $\text{[math]}$ 表示的数为．

答案解析收藏纠错 + 选题
12. 如图，以数轴的单位长度线段为边作一个正方形，以表示数2的点为圆心，正方形对角线长为半径画半圆，交数轴于点A和点B，则点A表示的数是；点B表示的数是．

答案解析收藏纠错 + 选题
13. (2020八上·萍乡期末) 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的大小关系用“＜”号排列为．

答案解析收藏纠错 + 选题
14. (2023七下·仙桃期末) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．若n为整数且 $\text{[math]}$ ，则n的值为．

答案解析收藏纠错 + 选题
15. (2024八下·惠阳月考) 阅读下列材料：因为 $\text{[math]}$ ，即 $\text{[math]}$ ，所以 $\text{[math]}$ 的整数部分为2，小数部分为 $\text{[math]}$ ，若规定实数m的整数部分记为 $\text{[math]}$ ，小数部分记为 $\text{[math]}$ ，可得： $\text{[math]}$ ， $\text{[math]}$ ．按照此规定计算 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题

三、解答题（共8题，共70分）

16. 课堂上老师讲解了比较 $\text{[math]}$ 和 $\text{[math]}$ 的方法，观察发现11-10＝15-14＝1，于是比较这两个数的倒数：
$\text{[math]}$

$\text{[math]}$

因为 $\text{[math]}$ ，所以 $\text{[math]}$ ，则有 $\text{[math]}$ ，

请你设计一种方法比较 $\text{[math]}$ 与 $\text{[math]}$ 的大小，

答案解析收藏纠错 + 选题
17. (2023七下·固始期末) 下面是小李同学探索 $\text{[math]}$ 的近似数的过程：
∵面积为107的正方形边长是 $\text{[math]}$ ，且 $\text{[math]}$ ，
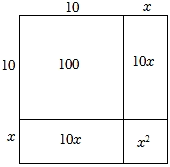
∴设 $\text{[math]}$ ，其中0＜x＜1，画出如图示意图，
∵图中S_正方形＝10²+2×10•x+x² ， S_正方形＝107
∴10²+2×10•x+x²＝107
当x²较小时，省略x² ，得20x+100≈107，得到x≈0.35，即 $\text{[math]}$ ．
1. （1） $\text{[math]}$ 的整数部分是；
2. （2）仿照上述方法，探究 $\text{[math]}$ 的近似值．（画出示意图，标明数据，并写出求解过程）
答案解析收藏纠错 + 选题
18. (2023七下·海淀月考) 阅读下面求 $\text{[math]}$ 近似值的方法，回答问题：
①任取正数 $\text{[math]}$ ；

②令 $\text{[math]}$ 则 $\text{[math]}$ ；

③ $\text{[math]}$ ，则 $\text{[math]}$ ；

……以此类推 $\text{[math]}$ 次，得到 $\text{[math]}$

其中 $\text{[math]}$ 称为 $\text{[math]}$ 的 $\text{[math]}$ 阶过剩近似值， $\text{[math]}$ 称为 $\text{[math]}$ 的 $\text{[math]}$ 阶不足近似值.仿照上述方法，求6的近似值.

①取正数 $\text{[math]}$ .

②于是 a₂= ；则 $\text{[math]}$ $\text{[math]}$

③ $\text{[math]}$ 的3阶过剩近似值 $\text{[math]}$ 是，3阶不足近似值是

答案解析收藏纠错 + 选题
19. 阅读下面材料：随着人们认识的不断深入，毕达哥拉斯学派逐渐承认 $\text{[math]}$ 不是有理数，并给出了证明．假设是 $\text{[math]}$ 有理数，那么存在两个互质的正整数p，q，使得 $\text{[math]}$ = $\text{[math]}$ ，于是p= $\text{[math]}$ q，两边平方得p²=2q² ．因为2q²是偶数，所以p²是偶数，而只有偶数的平方才是偶数，所以p也是偶数．因此可设p=2s，代入上式，得4s²=2q² ，即q²=2s² ，所以q也是偶数，这样，p和q都是偶数，不互质，这与假设p，q互质矛盾，这个矛盾说明， $\text{[math]}$ 不能写成分数的形式，即 $\text{[math]}$ 不是有理数．
请你有类似的方法，证明 $\text{[math]}$ 不是有理数．

答案解析收藏纠错 + 选题
20. (2020七下·碑林期中) 操作探究：已知在纸面上有一数轴（如图所示）
1. （1）折叠纸面，使表示的点1与﹣1重合，则﹣2表示的点与表示的点重合；
2. （2）折叠纸面，使﹣1表示的点与3表示的点重合，回答以下问题：
  ①5表示的点与数表示的点重合；
  ② $\text{[math]}$ 表示的点与数表示的点重合；
  ③若数轴上A、B两点之间距离为9（A在B的左侧），且A、B两点经折叠后重合，此时点A表示的数是、点B表示的数是
3. （3）已知在数轴上点A表示的数是a，点A移动4个单位，此时点A表示的数和a是互为相反数，求a的值.
答案解析收藏纠错 + 选题
21. (2022七上·海曙期中) 对于任何实数 $\text{[math]}$ ，可用 $\text{[math]}$ 表示不超过 $\text{[math]}$ 的最大整数，如 $\text{[math]}$ .
1. （1）则 $\text{[math]}$ ； $\text{[math]}$ ；
2. （2）现对119进行如下操作： $\text{[math]}$ ，这样对119只需进行3次操作后变为1.
  $\text{[math]}$ 对15进行1次操作后变为 ▲ ，对200进行3次操作后变为 ▲ ；
  
  $\text{[math]}$ 对实数 $\text{[math]}$ 恰进行2次操作后变成1，则 $\text{[math]}$ 最小可以取到 ▲ ；
  
  $\text{[math]}$ 若正整数 $\text{[math]}$ 进，3次操作后变为1，求 $\text{[math]}$ 的最大值.
答案解析收藏纠错 + 选题
22. (2020七上·杭州月考) 数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础.小白在草稿纸上画了一条数轴进行操作探究：
1. （1）操作一：折叠纸面，若使表示的点1与﹣1表示的点重合，则﹣2表示的点与表示的点重合；
2. （2）操作二：折叠纸面，若使1表示的点与﹣3表示的点重合，回答以下问题：
  ① $\text{[math]}$ 表示的点与数表示的点重合；
  
  ②若数轴上A、B两点之间距离为8（A在B的左侧），且A、B两点经折叠后重合，则A、B两点表示的数分别是；
3. （3）操作三：在数轴上剪下9个单位长度（从﹣1到8）的一条线段，并把这条线段沿某点折叠，然后在重叠部分某处剪一刀得到三条线段（如图）. 若这三条线段的长度之比为1：1：2，则折痕处对应的点所表示的数可能是.
答案解析收藏纠错 + 选题
23. (2020八下·临汾月考) 如图，在数轴上有两个长方形ABCD和EFGH，这两个长方形的宽都是2 $\text{[math]}$ 个单位长度，长方形ABCD的长AD是4 $\text{[math]}$ 个单位长度，长方形EFGH的长EH是8 $\text{[math]}$ 个单位长度，点E在数轴上表示的数是5 $\text{[math]}$ ，且E、D两点之间的距离为12 $\text{[math]}$ 。
1. （1）点H在数轴上表示的数是点，点A在数轴上表示的数是。
2. （2）若线段AD的中点为M，线段EH上有一点N，EN= $\text{[math]}$ EH，M以每秒4个单位长度的速度向右匀速运动，N以每秒3个单位长度的速度向左运动，设运动的时间为x秒，问当x为多少时，原点O恰为线段MN的三等分点？
3. （3）若线段AD的中点为M，线段EH上有一点N，EN= $\text{[math]}$ EH，长方形ABCD以每秒4个单位长度的速度向右匀速运动，长方形EFGH保持不动，设运动时间为t秒，是否存在一个t的值，使以M、N、F三点为顶点的三角形是直角三角形？若存在，求t的值；不存在，请说明理由。
答案解析收藏纠错 + 选题