 B .
B .  C .
C .  D .
D . 


⑴△ABC与△A1B1C1关于原点O对称,写出△A1B1C1各顶点的坐标,画出△A1B1C1;
⑵以O为旋转中心将△ABC顺时针旋转90°得△A2B2C2 , 画出△A2B2C2并写出△A2B2C2各顶点的坐标.
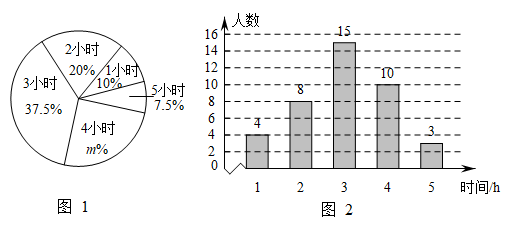
请根据图中提供的信息,解答下面的问题:
|
销售量 |
|
32.5 |
35 |
35.5 |
38 |
|
|
售价 |
|
27.5 |
25 |
24.5 |
22 |
|
