广西贵港市港南区2023-2024学年九年级上学期期中数学试...

更新时间：2024-03-27 浏览次数：20 类型：期中考试

一、选择题（本大题共12小题，每小题3分，共36分）

1. (2024九上·沂水期末) $\text{[math]}$ 的值等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . 2

答案解析收藏纠错 + 选题
2. (2024八下·宁明期末) 若一元二次方程mx²+2x+1＝0有实数解，则m的取值范围是（）

A . m≥-1 B . m≤1 C . m≥-1且m≠0 D . m≤1且m≠0

答案解析收藏纠错 + 选题
3. (2024九上·青县期末) 用电器的输出功率P与通过的电流I、用电器的电阻R之间的关系是P=I²R，下面说法正确的是（）

A . P为定值，I与R成反比例 B . P为定值，I²与R成反比例 C . P为定值，I与R成正比例 D . P为定值，I²与R成正比例

答案解析收藏纠错 + 选题
4. (2023九上·港南期中) 已知a ， b是一元二次方程x²-3x-2＝0的两根，则 $\text{[math]}$ 的值是（　　）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . -3

答案解析收藏纠错 + 选题
5. (2023九上·港南期中) 公元前3世纪，古希腊科学家阿基米德发现了杠杆平衡，后来人们把它归纳为“杠杆原理”，即：阻力×阻力臂＝动力×动力臂．小伟欲用撬棍撬动一块石头，已知阻力和阻力臂分别是1200N和0.5m ，则动力F（单位：N）关于动力臂l（单位：m）的函数解析式正确的是（　　）

A . F＝ $\text{[math]}$ B . F＝ $\text{[math]}$ C . F＝ $\text{[math]}$ D . F＝ $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023九上·港南期中) 正比例函数y=kx的图象经过点（3，2），则它与x轴所夹锐角的正弦值是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九上·南山期中) 近年来，由于新能源汽车的崛起，燃油汽车的销量出现了不同程度的下滑，经销商纷纷开展降价促销活动．某款燃油汽车今年3月份售价为23万元，5月份售价为16万元．设该款汽车这两月售价的月均下降率是x ，则所列方程正确的是（　　）

A . 16（1+x）²＝23 B . 23（1-x）²＝16 C . 23-23（1-x）²＝16 D . 23（1-2x）＝16

答案解析收藏纠错 + 选题
8. (2023九上·港南期中) 对于实数a ， b定义运算“※”为a※b＝b²-ab ，例如3※2＝2²-3×2＝-2．若关于x的方程3※x＝-m没有实数根，则m的值可以是（　　）

A . 3 B . 2 C . 1 D . 0

答案解析收藏纠错 + 选题
9. (2023九上·港南期中) 如图，在外力的作用下，一个滑块沿坡度为i＝1：3的斜坡向上移动了10米．此时滑块上升的高度是（　　）（单位：米）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 10

答案解析收藏纠错 + 选题
10. (2023九上·南京月考) 小明用地理中所学的等高线的知识在某地进行野外考察，他根据当地地形画出了“等高线示意图”，如图所示（注：若某地在等高线上，则其海拔就是其所在等高线的数值；若不在等高线上，则其海拔在相邻两条等高线的数值范围内），若A ， B ， C三点均在相应的等高线上，且三点在同一直线上，则 $\text{[math]}$ 的值为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
11. (2023九上·港南期中) 如图，一辆自行车竖直摆放在水平地面上，右边是它的部分示意图，测得AB＝60cm ， ∠B＝50°，则点A到BC的距离为（　　）

A . 60sin50°cm B . 60cos50°cm C . $\text{[math]}$ D . 60tan50°cm

答案解析收藏纠错 + 选题
12. (2023九上·港南期中) 阅读材料：余弦定理是描述三角形中三边长度与一个角余弦值关系的数学定理，运用它可以解决一类已知三角形两边及夹角求第三边或者已知三边求角的问题．余弦定理是这样描述的：在△ABC中，∠A、∠B、∠C所对的边分别为a、b、c ，则三角形中任意一边的平方等于另外两边的平方和减去这两边及这两边的夹角的余弦值的乘积的2倍．用公式可描述为：a²＝b²+c²-2bccosA；b²＝a²+c²-2accosB；c²＝a²+b²-2abcosC ．现已知在△ABC中，AB＝2，BC＝4，∠A＝60°，则AC的长为（　　）

A . 2 $\text{[math]}$ B . $\text{[math]}$ +1 C . $\text{[math]}$ -1 D . 3 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题2分，共12分）

13. (2023九上·港南期中) 已知线段a＝9，b＝4，则线段a和b的比例中项为．

答案解析收藏纠错 + 选题
14. (2023九上·港南期中) 若反比例函数的图象经过点（1，m² ），（2，n），则n的取值范围为．

答案解析收藏纠错 + 选题
15. (2023九上·港南期中) 已知方程x²-5x-2＝0的两根分别为x₁ ， x₂ ，则 $\text{[math]}$ ＝．

答案解析收藏纠错 + 选题
16. (2024九下·望奎月考) △AOB三个顶点的坐标分别为A（5，0），O（0，0），B（3，6），以原点O为位似中心，相似比为 $\text{[math]}$ ，将△AOB缩小，则点B的对应点B^'的坐标是．

答案解析收藏纠错 + 选题
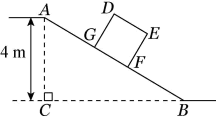
17. (2023九上·港南期中) 某仓储中心有一斜坡AB，其坡比i＝1：2，顶部A处的高AC为4米，B、C在同一水平面上.则斜坡AB的水平宽度BC为米.

答案解析收藏纠错 + 选题
18. (2024七下·思明期末) 生物工作者为了估计一片山林中雀鸟的数量，设计了如下方案：先捕捉50只雀鸟，给它们做上标记后放回山林；一段时间后，再从山林中随机捕捉80只，其中有标记的雀鸟有2只，请你帮助工作人员估计这片山林中雀鸟的数量为只．

答案解析收藏纠错 + 选题

三、解答题（本大题共8小题，满分72分.解答应写出文字说明、证明过程或演算步骤.）

19. (2023九上·港南期中) 计算：3tan30°+tan45°-2sin60°．

答案解析收藏纠错 + 选题
20. (2023九上·港南期中) 解方程： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2023九上·禹城月考) 已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示：
1. （1）求电流I关于电阻R的函数解析式；
2. （2）如果以此蓄电池为电源的用电器的限制电流I不能超过10A ，请直接写出该用电器可变电阻R应控制在什么范围？
答案解析收藏纠错 + 选题
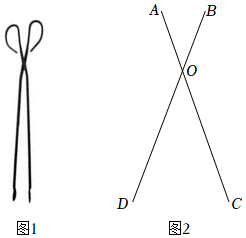
22. (2023九上·港南期中) 火钳是铁制夹取柴火的工具，有保洁员拿它拾捡地面垃圾使用，图1是火钳实物图，图2是其示意图．已知火钳打开最大时，两钳臂OC ， OD的夹角∠COD＝40°，若OC＝OD＝40cm ，求两钳臂端点C ， D的距离．（结果精确到1cm ，参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）

答案解析收藏纠错 + 选题
23. (2023九上·港南期中) 某商场以每件20元的价格购进一种商品，规定这种商品每件售价不低于进价，又不高于38元，经市场调查发现：该商品每天的销售量y（件）与每件售价x（元）之间符合一次函数关系，如图．
1. （1）求y与x之间的函数关系式；
2. （2）该商场销售这种商品要想每天获得600元的利润，每件商品的售价应定为多少元？
答案解析收藏纠错 + 选题
24. (2023九上·港南期中) “黄金三角形”是几何历史上的瑰宝，它有两种类型，其中一种是顶角为36°的等腰三角形，如图，在△ABC中，∠A＝36°，AB＝AC ．
1. （1）实践与操作：利用尺规作∠B的平分线，交边AC于点D（要求：尺规作图并保留作图痕迹，不写作法，标明字母）；
2. （2）猜想与证明：请你利用所学知识，证明点D是边AC的黄金分割点．
答案解析收藏纠错 + 选题
25. (2023九上·港南期中) 如图1是一个简易手机支架，由水平底板 $\text{[math]}$ 、侧支撑杆 $\text{[math]}$ 和手机托盘长 $\text{[math]}$ 组成，侧面示意图如图2所示.已知手机托盘长 $\text{[math]}$ ，侧支撑杆 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，其中点A为手机托盘最高点，支撑点B是 $\text{[math]}$ 的中点，手机托盘 $\text{[math]}$ 可绕点B转动，侧支撑杆 $\text{[math]}$ 可绕点D转动.
1. （1）如图2，求手机托盘最高点A离水平底板 $\text{[math]}$ 的高度h（精确到 $\text{[math]}$ ）.
2. （2）如图3，当手机托盘 $\text{[math]}$ 绕点B逆时针旋转 $\text{[math]}$ 后，再将 $\text{[math]}$ 绕点D顺时针旋转 $\text{[math]}$ ，使点C落在水平底板 $\text{[math]}$ 上，求 $\text{[math]}$ （精确到0.1 $\text{[math]}$ ）.（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
答案解析收藏纠错 + 选题
26. (2023九上·港南期中) 学校“华罗庚数学”社团对函数y＝2|x-2|-1的图象和性质进行了探究，请把以下探究过程补充完整．
1. （1）自变量x的取值范围是全体实数，x与y的几组值列表如下：
  x
  …
  -1
  0
  1
  2
  3
  4
  5
  …
  y
  …
  5
  3
  1
  1
  3
  5
  …
2. （2）请在平面直角坐标系中，把表中的数对（x ， y）进行描点，并画出函数图象；
3. （3）观察函数图象，写出一条函数图象的性质：；
4. （4）进一步探究函数图象发现：
  ①函数图象与x轴有个交点，对应的方程2|x-2|-1＝0有个实数根；
  ②若关于x的方程2|x-2|-1＝a有两个实数根，则a的取值范围是．
答案解析收藏纠错 + 选题