北师大版数学七年级上册期末冲刺满分攻略13 整式的认识及其运...

更新时间：2024-01-01 浏览次数：55 类型：复习试卷

一、选择题

1. (2023七上·宝安期中) 已知a ， b ， c在数轴上对应的点如图所示，则代数式 $\text{[math]}$ 化简后的结果为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2b D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023七上·江城期中) 如果a和-4b互为相反数，那么多项式2(-b-2a+10)+3(a+2b-3)的值是（）

A . 11 B . 29 C . 0 D . 9

答案解析收藏纠错 + 选题
3. (2023七上·中山期中) 两艘船从同一港口出发，甲船顺水而下，乙船逆水而上，已知两船在静水中的速度都是45km/h，水流速度是akm/h，1h后两船相距（）km.

A . 90 B . 4a C . 2a D . 180

答案解析收藏纠错 + 选题
4. 把多项式x³-xy²+x²y+x⁴-3按x的降幂排列是( )

A . x⁴+x³+x²y-3-xy² B . -xy²+x²y+x⁴+x³-3 C . -3-xy²+x²y+x³+x⁴ D . x⁴+x³+x²y-xy²-3

答案解析收藏纠错 + 选题
5. (2022七上·龙岗期末) 若单项式 $\text{[math]}$ 与 $\text{[math]}$ 是同类项，则 $\text{[math]}$ 的值是（）

A . -6 B . -4 C . 9 D . 4

答案解析收藏纠错 + 选题
6. (2023七上·广州期中) 下列运算结果不正确的有（）
①2a+b=2ab；②4a²-a²=3；③-x²-x²=-2x²；④5mn-5n=m

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
7.
下图是一个数值转换机，若输入的x为–7，则输出的结果是（）

A . 12 B . -14 C . 27 D . 21

答案解析收藏纠错 + 选题
8.
如图1，将一个边长为a的正方形纸片剪去两个矩形，得到一个“S”的图案，如图2所示，再将剪下的两个小矩形拼成一个新的矩形，如图3所示，则新矩形的周长可表示为（　　）

A . 2a﹣3b B . 2a﹣4b C . 4a﹣8b D . 4a﹣10b

答案解析收藏纠错 + 选题
9. (2023七上·福田期中) 下列说法中，不正确的是（）

A . 若a和b都是负数，且|a|＞|b|，则a＜b B . -2xyz³的系数是-2，次数是5 C . 若a和b都是正数，且|a|＞|b|，则a＞b D . πd+2πR是二次二项式

答案解析收藏纠错 + 选题
10. (2023七上·深圳期中) 代数式 $\text{[math]}$ ， 2x+y ， $\text{[math]}$ a²b ， $\text{[math]}$ ， 0.5， $\text{[math]}$ 中整式的个数为（　　）

A . 3个 B . 4个 C . 5个 D . 6个

答案解析收藏纠错 + 选题

二、填空题

11. (2023七上·福田期中) 若多项式x^|^m^-3|-8x²+（m-7）x是关于x的四次三项式，则m的值为．

答案解析收藏纠错 + 选题
12. 长为3m+2n，宽为5m﹣n的长方形的面积为

答案解析收藏纠错 + 选题
13. (2023七上·广州期中) 化简-x²+x-2-（-x²+1）=．

答案解析收藏纠错 + 选题
14. 定义一种新运算：a※b= $\text{[math]}$ ，则当x=3时，2※x﹣4※x的结果为

答案解析收藏纠错 + 选题
15. (2020七上·江门月考) 已知a ， b ， c在数轴上的位置如图所示，则 $\text{[math]}$ =

答案解析收藏纠错 + 选题
16. (2022七上·南山期中) 如图，将边长为4的正方形和半径为2的圆叠放在一起，两个空白部分的面积分别为m，n（m＞n），则m-n的值为（结果保留π）．

答案解析收藏纠错 + 选题

三、解答题

17. (2023七上·惠城期中) 化简：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2023七上·吉安期中) 已知代数式 $\text{[math]}$ ，代数式 $\text{[math]}$ ，代数式 $\text{[math]}$ .
1. （1）化简代数式C；
2. （2）若代数式C的值与y的取值无关，求x的值.
答案解析收藏纠错 + 选题
19. (2024七上·交城期中) 如图，长为 $\text{[math]}$ ，宽为 $\text{[math]}$ 的长方形被分割成7个部分，除两个阴影图形M，N外，其余的5个部分为形状和大小完全相同的小长方形，其中小长方形的宽为3.
1. （1）求小长方形的长（用含 $\text{[math]}$ 的代数式表示）；
2. （2）希望小组的同学们发现阴影图形M和阴影图形N的周长之和与 $\text{[math]}$ 的值无关，希望小组的判断是否正确，请说明理由.
答案解析收藏纠错 + 选题
20. (2023七上·中山期中) 如图，已知数轴上两点A、B.点C为数轴上的动点，其表示的数为x.
1. （1）若点C到点A、B的距离相等，则点C表示的数x的值为；
2. （2）式子|x-3|+|x+1|的最小值是；
3. （3）点D也是数轴上的一个动点，已知点C的运动速度为每秒2个单位长度，动点C、D同时分别从点A、B出发开始运动.
  ①若点C、D相向而行，在表示数 $\text{[math]}$ 的点相遇，求点D的运动速度；
  ②若点D的运动速度是每秒4个单位长度，C、D两点同时向左匀速运动，则当C、D两点之间的距离为2时，两点运动了多长时间?
4. （4）若动点C从点A出发，第一次向左运动1个单位长度，第二次向右运动2个单位长度，第三次向左运动3个单位长度，…，按此规律不断在数轴上做往复运动，当点C运动了n次时，直接用含n的代数式表示出点C所表示的有理数.
答案解析收藏纠错 + 选题
21. (2023七上·威远期中) 将连续的奇数1，3，5，7，9…排成如图所示的数阵，用十字框按如图所示的方式任意框五个数.（十字框只能平移）
1. （1）若框住的5个数中，正中间的一个数为17，则这5个数的和为.
2. （2）设正中间的数为a ，用式子表示十字框内五个数的和.
3. （3）十字框能否框住这样的5个数，它们的和等于2035？若能，求出正中间的数a；若不能，请说明理由.
答案解析收藏纠错 + 选题
22. (2023七上·西安期末) 某公司生产一种电子产品和配件，已知该电子产品的售价为200元/台，配件的售价为20元/个，在促销活动期间，有如下两种优惠方案（顾客只能选择其中一种优惠方案）：
①买一台电子产品送一个配件；
②电子产品每台降价10元出售，配件每个打9折.
在促销活动期间，某学校计划到该公司购买 $\text{[math]}$ 台电子产品， $\text{[math]}$ 个配件 $\text{[math]}$ .
1. （1）分别求该校选择优惠方案①，②购买该电子产品和配件所需的总费用；（用含x、y的代数式来表示）
2. （2）若该校计划购买该电子产品10台，配件20个，请通过计算判断，选择哪种优惠方案更省钱？
答案解析收藏纠错 + 选题
23. (2023七上·黄埔期中)
1. （1）阅读材料：我们知道，4x+2x-x=（4+2-1）x=5x ，类似地，我们把（a+b）看成一个整体，则4(a+b)+2(a+b)-(a+b)=(4+2-1)(a+b)=5(a+b).“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛。
  尝试应用：
  ①把(a+b)²看成一个整体，合并-3(a+b)²-6(a+b)²+8(a+b)²的结果 ▲ .
  ②拓广探索：已知a-2b=5，2b-c=-7，c-d=12，求4(a-c)+4(2b-d)-4(2b-c)的值.
2. （2）某人用400元购买了8套电子产品，准备以一定价格出售，如果每套电子产品以56元的价格作为标准卖出，超出的记为正数，不足的记为负数，记录如下（单位：元）：
  -3，+7，-8，+9，-2，0，-1，-6，
  当他卖完这8套电子产品后是盈利还是亏损？
答案解析收藏纠错 + 选题
24. (2023七上·济南期中) 阅读材料，回答问题．
材料一：因为2³=2×2×2，2²=2×2，所以2³×2²=(2×2×2)×(2×2)=25.
材料二：求3¹+3²+3³+3⁴+3⁵+3⁶的值.
解：设S=3¹+3²+3³+3⁴+3⁵+3⁶①
则3S=3²+3³+3⁴+3⁵+3⁶+3⁷②
用②－①得，3S－S=(3²+3³+3⁴+3⁵+3⁶+3⁷)－(3¹+3²+3³+3⁴+3⁵+3⁶)=3⁷－3
所以2S=3⁷－3，即S= $\text{[math]}$
所以3¹+3²+3³+3⁴+3⁵+3⁶= $\text{[math]}$
这种方法我们称为"错位相减法".
1. （1）填空：5×5⁸=5^（^）， a²·a⁵=a^（^）.
2. （2） "棋盘摆米"是一个著名的数学故事：阿基米德与国王下棋，国王输了，国王问阿基米德要什么奖赏．阿基米德对国王说："我只要在棋盘上第一格放一粒米，第二格放二粒，第三格放四粒，第四格放八粒…按这个方法放满整个棋盘就行"国王以为要不了多少粮食，就随口答应了．
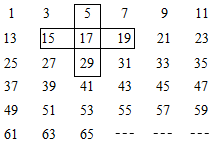
  ①国际象棋共有64个格子，则在第64格中应放 ▲ 粒米．（用幂表示）
  ②设国王输给阿基米德的总米粒数为S，求S.
答案解析收藏纠错 + 选题