【培优卷】3.4圆周角和圆心角的关系—2023-2024学年...

更新时间：2024-01-14 浏览次数：45 类型：同步测试

一、选择题

1. (2023九上·滨江月考) 如图，四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点E，若 $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·十堰) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的外接圆，弦 $\text{[math]}$ 交 $\text{[math]}$ 于点E， $\text{[math]}$ ， $\text{[math]}$ ，过点O作 $\text{[math]}$ 于点F，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点G，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . 7 C . 8 D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九下·武汉月考) 如图，AB为⊙O的直径，BC是弦，将 $\text{[math]}$ 绕着A点顺时针旋转得到 $\text{[math]}$ ，点D恰好落在⊙O上，AB交 $\text{[math]}$ 于E点，若OE＝EB，AB＝4，则BC的长是（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·玉环模拟) 如图，四边形 $\text{[math]}$ 为正方形，其中分别以 $\text{[math]}$ 为直径在正方形内部做半圆，正方形的对角线交于O点，点E是以 $\text{[math]}$ 为直径的半圆上的一个动点，则下列结论错误的是（）

A . 若正方形的边长为10，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为 $\text{[math]}$ B . 连接 $\text{[math]}$ ，则 $\text{[math]}$ C . 连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则正方形的边长为 $\text{[math]}$ D . 若M，N分别为 $\text{[math]}$ 的中点，存在点E，使得 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022·易县模拟) 如图，MN是⊙O的直径，MN＝4，∠AMN＝30°，点B为弧AN的中点，点P是直径MN上的一个动点，则PA+PB的最小值为（）

A . 4 B . 4 $\text{[math]}$ C . 2 $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
6. (2022九下·淮北月考) 等腰△ABC中，AB＝AC，以腰AB为直径的圆O，与底边BC交于P，若圆O与腰AC的交点Q关于直线AP的对称点落在线段OA上（不与端点重合），则下列说法正确的是（）

A . ∠BAC＞60° B . 30°＜∠ABC＜60° C . BP＞ $\text{[math]}$ AB D . $\text{[math]}$ AC＜PQ＜ $\text{[math]}$ AC

答案解析收藏纠错 + 选题
7. (2023·博乐模拟) 如图， $\text{[math]}$ 内接于半径为 $\text{[math]}$ 的半圆 $\text{[math]}$ 中， $\text{[math]}$ 为直径，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，连结 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的中点，可得（    ）

① $\text{[math]}$     ② $\text{[math]}$     ③ $\text{[math]}$     ④ $\text{[math]}$

A . ①②③ B . ①②④ C . ①③④ D . ②③④

答案解析收藏纠错 + 选题
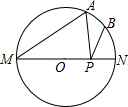
8. (2022九下·惠山期中) 我们定义：两边平方和等于第三边平方的2倍的三角形叫做奇异三角形，根据定义：①等边三角形一定是奇异三角形；②在Rt△ABC中，∠C＝90°，AB＝c，AC＝b，BC＝a，且b＞a，若Rt△ABC是奇异三角形，则a：b：c＝1： $\text{[math]}$ ：2；③如图，AB是⊙O的直径，C是⊙O上一点（不与点A、B重合），D是半圆 $\text{[math]}$ 的中点，C、D在直径AB的两侧，若在⊙O内存在点E，使AE＝AD，CB＝CE．则△ACE是奇异三角形；④在③的条件下，当△ACE是直角三角形时，∠AOC＝120°，其中，说法正确的有（）

A . ①② B . ①③ C . ②④ D . ③④

答案解析收藏纠错 + 选题

二、填空题

9. (2023·慈溪模拟) 如图，在平面直角坐标系xOy中，点B在x轴正半轴上，点D在y轴正半轴上，⊙C经过A，B，D，O四点，∠OAB＝120°，OB＝4 $\text{[math]}$ ，则点D的坐标是．

答案解析收藏纠错 + 选题
10. (2023·红花岗模拟) 已知 $\text{[math]}$ 内接于 $\text{[math]}$ ，它的内心为点 $\text{[math]}$ ，连接 $\text{[math]}$ 交弦 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则线段 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
11. (2022·凤县模拟) 如图，正方形ABCD的边长是4，F点是BC边的中点，点H是CD边上的一个动点，以CH为直径作 $\text{[math]}$ ，连接HF交 $\text{[math]}$ 于E点，连接DE，则线段DE的最小值为.

答案解析收藏纠错 + 选题
12. (2022·乐清模拟) 如图， $\text{[math]}$ 内接于⊙O， $\text{[math]}$ ， $\text{[math]}$ 外角 $\text{[math]}$ 的平分线交⊙O于点D，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为.

答案解析收藏纠错 + 选题

三、综合题

13. 如图， $\text{[math]}$ 都是 $\text{[math]}$ 的半径， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的半径．
答案解析收藏纠错 + 选题
14. (2023·安徽) 已知四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ，对角线 $\text{[math]}$ 是 $\text{[math]}$ 的直径．
1. （1）如图1，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，求证； $\text{[math]}$ 平分 $\text{[math]}$ ；
2. （2）如图2， $\text{[math]}$ 为 $\text{[math]}$ 内一点，满足 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，求弦 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
15. (2023·湛江模拟) 在学习《圆》这一单元时，我们学习了圆周角定理的推论：圆内接四边形的对角互补；事实上，它的逆命题：对角互补的四边形的四个顶点共圆，也是一个真命题．在图形旋转的综合题中经常会出现对角互补的四边形，那么，我们就可以借助“对角互补的四边形的四个顶点共圆”，然后借助圆的相关知识来解决问题，例如：已知： $\text{[math]}$ 是等边三角形，点D是 $\text{[math]}$ 内一点，连接 $\text{[math]}$ ，将线段 $\text{[math]}$ 绕C逆时针旋转 $\text{[math]}$ 得到线段 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，并延长 $\text{[math]}$ 交 $\text{[math]}$ 于点F．当点D在如图所示的位置时：
1. （1）观察填空：与 $\text{[math]}$ 全等的三角形是；
2. （2）利用（1）中的结论，求 $\text{[math]}$ 的度数
3. （3）判断线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系，并说明理由．
答案解析收藏纠错 + 选题