一、单选题:(本大题共8小题,每小题5分,共40 分.在每小题四个选项中 ,只有一项是符合题目要求的)
-
-
A . 若向量 ,
,  共线,则向量
共线,则向量 ,
,  所在的直线平行
B . 若向量
所在的直线平行
B . 若向量 ,
,  所在的直线为异面直线,则向量
所在的直线为异面直线,则向量 ,
,  一定不共面
C . 若存在不全为0的实数
一定不共面
C . 若存在不全为0的实数 使得
使得 , 则
, 则 ,
,  ,
,  共面
D . 对于空间的任意一个向量
共面
D . 对于空间的任意一个向量 , 总存在实数
, 总存在实数 使得
使得
-
-
4.
(2023高二上·闽清月考)
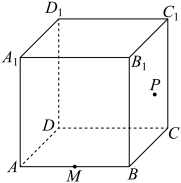
如图,已知正方体

的棱长为1,点
M为棱

的中点,点
P在正方形

的边界及其内部运动.给出以下四个结论:
①存在点P满足 ;
;
②存在点P满足 ;
;
③满足 的点P的轨迹长度为
的点P的轨迹长度为 ;
;
④满足 的点P的轨迹长度为
的点P的轨迹长度为 .
.
其中正确的结论的个数为( )
A . 1
B . 2
C . 3
D . 4
-
-
6.
(2023高二上·闽清月考)
数学美的表现形式不同于自然美或艺术美那样直观,它蕴藏于特有的抽象概念,公式符号,推理论证,思维方法等之中,揭示了规律性,是一种科学的真实美. 平面直角坐标系中, 曲线
C:

就是一条形状优美的曲线,对于此曲线,给出如下结论:
①曲线C围成的图形的面积是 
②曲线C围成的图形有2条对称轴;
③曲线C上的任意两点间的距离不超过2;
④若P(m , n)是曲线C上任意一点,则  的最小值是
的最小值是 
其中正确结论的个数为( )
A . 1
B . 2
C . 3
D . 4
-
7.
(2023高二上·闽清月考)
已知椭圆的方程为

分别为椭圆的左、右焦点,

为椭圆上在第一象限的一点,

为

的内心,直线

与

轴交于点

, 若

, 则该椭圆的离心率为( )
-
二、多选题(本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中 ,有多项是符合题目要求的。正确选项全对得5分,正确选项不全得2分,有错误选项得0分)
三、填空题:本大题共4小题,每小题5分,共20分。
四、解答题:本大题共6小题,共70 分.解答应写出文字说明,证明过程或演算步骤。
-
-
-
(2)
求异面直线

与

所成角的余弦值.
-
-
(1)
在线段

上是否存在点
N , 使得

恒成立,若存在,求出点
N的位置,若不存在,说明理由;
-
(2)
当点
M落在线段

靠近

点

上时,求二面角

的余弦值.
-
-
(1)
求圆

的方程;
-
(2)
已知斜率为

的直线

经过第三象限,且与圆

交于点

, 求

的面积的取值范围.
-
20.
(2023高二上·闽清月考)
在平面直角坐标系

中,已知两点

, 动点

满足

, 设点

的轨迹为

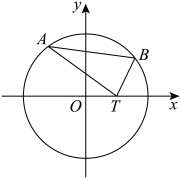
.如图,动直线

与曲线

交于不同的两点

(

均在

轴上方),且

.
-
(1)
求曲线

的方程;
-
(2)
当

为曲线

与

轴正半轴的交点时,求直线

的方程;
-
(3)
是否存在一个定点,使得直线

始终经过此定点?若存在,求出定点的坐标;若不存在,请说明理由.
-
-
-
(2)
求
O到直线

的距离的范围.
-
-
-
(2)
设双曲线左右顶点分别为

, 在直线

上取一点

, 直线

交双曲线右支于点

, 直线

交双曲线左支于点

, 直线

和直线

的交点为

, 求证:点

在定直线上.
;
;
的点P的轨迹长度为
;
的点P的轨迹长度为
.

的最小值是