【培优卷】2024年浙教版数学八年级下册3.3 方差和标准差

更新时间：2024-03-02 浏览次数：20 类型：同步测试

一、选择题

1. (2023八上·文登期中) 一组数据的方差计算公式为： $\text{[math]}$ ，下列关于这组数据的说法错误的是（）

A . 平均数是7 B . 中位数是6.5 C . 众数是6 D . 方差是1

答案解析收藏纠错 + 选题
2. 已知一组数据的方差为 $\text{[math]}$ ，数据为：－1，0，3，5，x，那么x等于（）

A . －2或5.5 B . 2或－5.5 C . 4或11 D . －4或－11

答案解析收藏纠错 + 选题
3. (2024八上·罗湖期末) 在“经典诵读”比赛活动中，某校10名学生参赛成绩如图所示，对于这10名学生的参赛成绩，下列说法正确的是（）

A . 众数是90分 B . 中位数是95分 C . 平均数是95分 D . 方差是15

答案解析收藏纠错 + 选题
4. (2024九下·昆明模拟) 已知一组数据， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的平均数是2，方差是3．则另一组数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，的平均数和方差分别是（）

A . 43 B . 427 C . 63 D . 627

答案解析收藏纠错 + 选题
5. (2023·唐山模拟) 若一组数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的平均数为4，方差为3，那么数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的平均数和方差分别是（）

A . 4， 3 B . 6 $\text{[math]}$ 3 C . 3 $\text{[math]}$ 4 D . 6 5

答案解析收藏纠错 + 选题
6. (2023八上·利津期末) 若样本x₁+1，x₂+1，…，x_n+1的平均数为10，方差为2，则对于样本x₁+2，x₂+2，…，x_n+2，下列结论正确的是（）

A . 平均数为10，方差为2 B . 平均数为11，方差为3 C . 平均数为11，方差为2 D . 平均数为12，方差为4

答案解析收藏纠错 + 选题
7. (2024·从江模拟) 一枚质地均匀的正方体骰子（六个面分别标有数字1，2，3，4，5，6），投掷5次，分别记录每次骰子向上的一面出现的数字．根据下面的统计结果，能判断记录的这5个数字中一定没有出现数字6的是（）

A . 中位数是3，众数是2 B . 平均数是3，中位数是2 C . 平均数是3，方差是2 D . 平均数是3，众数是2

答案解析收藏纠错 + 选题

二、填空题

8. 为迎接体育测试，小强每天坚持引体向上锻炼，他记录了某一周每天做引体向上的个数，如下表：

其中有三天的个数被墨汁覆盖了，但小强已经计算出这组数据唯一的众数是13，平均数是12，那么这组数据的方差是。

答案解析收藏纠错 + 选题
9. (2023九上·合肥开学考) 有一组数据：5，2， $\text{[math]}$ ， 5，2，6，它们的中位数是4.5，则这组数据的方差是.

答案解析收藏纠错 + 选题
10. 教练对跳远运动员小刚的训练效果进行了测试，6次跳远的成绩(单位：m)如下：7.6，7.8，7.7，7.8，8.0，7.9.这6次成绩的平均数是7.8m，方差是 $\text{[math]}$ m².若小刚再跳两次，成绩分别是7.7，7.9，则小刚这8次跳远成绩的方差将(填“变大”“变小”或“不变”).

答案解析收藏纠错 + 选题
11. (2021八下·鄞州期中) 如果一组按从小到大排序的数据a，b，c的平均数是b，方差是S² ，那么数据a+99，b+100，c+101的方差将 S²（填“大于”“小于”或“等于”）.

答案解析收藏纠错 + 选题

三、解答题

12. (2022七下·大庆期末) 省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，成绩如下表（单位：环）：甲：9；7；10；10；9；9；乙：10；8；9；8；10；9
1. （1）分别计算甲、乙六次测试成绩的平均数和方差；
2. （2）你认为推荐谁参加全国比赛更合适，说明理由．
答案解析收藏纠错 + 选题
13. (2023八下·朔州期末) 学校举办纪念“五四运动”104周年暨“青春心向党，建功新时代”演讲比赛．同学们用青春的声音和故事，激扬五四精神，彰显青春风采，展现拼搏风貌，深情地演绎了对党和祖国的热爱之情．

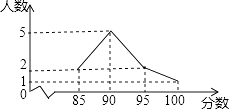
初赛阶段两个年级各10名选手的成绩统计如下：
七年级：98　96　86　85　84　94　77　69　59　94
八年级：99　96　73　82　96　79　65　96　55　96
他们的数据分析过程如下：
1. （1）整理、描述数据：根据上面得到的两组数据，分别绘制频数分布直方图如图：
  
  请补全八年级频数分布直方图；
2. （2）数据分析：两组数据的平均数、中位数、方差如表所示：
  年级
  平均数
  中位数
  方差
  七年级
  ①
  85.5
  144.36
  八年级
  83.7
  ②
  251.21
  根据以上数据求出表格中①，②两处的数据；
3. （3）推断结论：根据以上信息，判断哪个年级比赛成绩整体较好？说明理由（至少从两个不同角度说明判断的合理性）．
答案解析收藏纠错 + 选题

14.

（1）已知三组数据，通过计算完成填表：

数据	平均数	方差
1，2，3，4，5
11，12，13，14，15
3，6，9，12，15

（2）【分析数据】请你比较三组数据的大小及统计量的结果，写出其中一些规律性的结论。
（3）【解决问题】请你用发现的结论来解决以下的问题。

已知数据x₁ ， x₂ ， x₃ ， …，x_n的平均数为a，方差为b，则
（1）数据x₁+3，x₂+3，x₃+3，…，x_n+3的平均数为，方差为。
（2）数据x₁-3，x₂-3，x₃-3，…，x_n-3的平均数为，方差为。
（3）数据3x₁ ， 3x₂ ， 3x₃ ， …，3x_n的平均数为方差为。
（4）数据2x₁-3，2x₂-3，2x₃-3，…，2x_n-3的平均数为，方差为。

答案解析收藏纠错 + 选题

15. (2022·红塔模拟) 2021年12月，中共玉溪市红塔区委办公室、玉溪市红塔区人民政府办公室印发《玉溪市红塔区进一步减轻义务教育阶段学生作业负担和校外培训负担的实施方案》，文件明确要求，建立作业统筹管理机制，科学合理布置作业，严控作业总量和时长，切实减轻学生过重课业负担，初中学生每天书面作业平均完成时间不超过90分钟，周末、寒暑假、法定节假日也控制书面作业时间，某校为了解在“双减”政策下九年级学生每天书面作业完成时间（单位：分钟）的落实情况，在九年级学生中随机抽取部分学生进行了一次问卷调查，并将调查结果统计如下表：
每天书面完成时间t/分钟
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
人数
2
10
15
17
6
1. （1）直接写出本次调查的样本容量，中位数所在的范围及平均数（计算平均数时，可用各组的组中值代表各组的实际数据）；
2. （2）直接写出抽取的学生每天书面作业完成时间超过90分钟的人数，估计该校九年级学生每天书面作业平均完成时间是否符“双减”政策的要求，并说明理由．
答案解析收藏纠错 + 选题

16. (2019八下·铜陵期末) 某中学开展“唱红歌”比赛活动，九年级（1）、（2）班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩如图所示．

（1）根据图示填写下表；

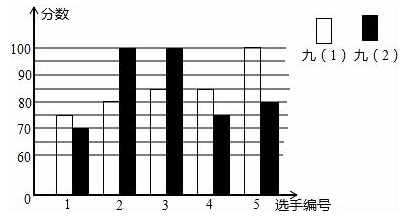
班级	平均数（分）	中位数（分）	众数（分）
九（1）		85
九（2）	85		100

（2）结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好；
（3）计算两班复赛成绩的方差．

答案解析收藏纠错 + 选题

17. (2020·福州模拟) 图1是某市2009年4月5日至14日每天最低气温的折线统计图．
1. （1）图2是该市2007年4月5日至14日每天最低气温的频数分布直方图，根据图1提供的信息，补全图2中频数分布直方图；
2. （2）在这10天中，最低气温的众数是，中位数是，方差是．
3. （3）请用扇形图表示出这十天里温度的分布情况．
答案解析收藏纠错 + 选题