广东省清远市2023-2024学年高二上学期期末教学质量检测...

更新时间：2024-11-07 浏览次数：6 类型：期末考试

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. (2024高二上·清远期末) 已知倾斜角为 $\text{[math]}$ 的直线 $\text{[math]}$ 与直线 $\text{[math]}$ 垂直，则 $\text{[math]}$ （）

A . 2 B . -2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高二上·清远期末) 椭圆 $\text{[math]}$ 上一点 $\text{[math]}$ 与它的一个焦点的距离等于4，则点 $\text{[math]}$ 与另一个焦点的距离等于（）

A . 2 B . 6 C . 8 D . 16

答案解析收藏纠错 + 选题
3. (2024高二上·清远期末) 已知等差数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 3 B . -3 C . 2 D . -2

答案解析收藏纠错 + 选题
4. (2024高二上·清远期末) 如图，在四棱锥 $\text{[math]}$ 中，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，设 $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高二上·清远期末) 2020年1月，教育部发布《关于在部分高校开展基础学科招生改革试点工作的意见》（简称“强基计划”），明确从2020年起强基计划取代原有的高校自主招生方式.某高校笔试环节要求考生参加三个科目考核，考生通过三个科目的笔试考核才能进入面试环节.考生甲通过三个科目的笔试考核的概率分别为 $\text{[math]}$ ，且每个科目考核相互独立，则甲顺利进入面试环节的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024高二上·清远期末) 已知空间向量 $\text{[math]}$ ，则下列说法正确的是（）

A . $\text{[math]}$ 是等腰直角三角形 B . $\text{[math]}$ ，则 $\text{[math]}$ 四点共面 C . 四边形 $\text{[math]}$ 是矩形 D . 若 $\text{[math]}$ 与 $\text{[math]}$ 分别是异面直线 $\text{[math]}$ 与 $\text{[math]}$ 的方向向量，则 $\text{[math]}$ 与 $\text{[math]}$ 所成角的余弦值为 $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024高二上·清远期末) 如图，在一个7行8列的数表中，第 $\text{[math]}$ 行第 $\text{[math]}$ 列的元素为 $\text{[math]}$ ，其中 $\text{[math]}$ ，则该数表中所有无重复的元素之和为（）
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高二上·清远期末) 如图，已知抛物线 $\text{[math]}$ 的焦点为 $\text{[math]}$ 为抛物线上两点，且有 $\text{[math]}$ ，直线 $\text{[math]}$ 与准线分别交于 $\text{[math]}$ 两点，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.

9. (2024高二上·清远期末) 已知数列 $\text{[math]}$ 满足 $\text{[math]}$ ，则下列结论成立的有（）

A . 数列 $\text{[math]}$ 为等差数列 B . 数列 $\text{[math]}$ 为递增数列 C . $\text{[math]}$ D . 数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024高二上·清远期末) 已知圆心为 $\text{[math]}$ 的圆经过 $\text{[math]}$ ，则（）

A . 圆 $\text{[math]}$ 的方程为 $\text{[math]}$ B . 圆 $\text{[math]}$ 上一点 $\text{[math]}$ 到点 $\text{[math]}$ 的距离为 $\text{[math]}$ ，则 $\text{[math]}$ C . 圆心为 $\text{[math]}$ ，半径为 $\text{[math]}$ 的圆与圆 $\text{[math]}$ 有公共点，则 $\text{[math]}$ D . 过点 $\text{[math]}$ 的直线 $\text{[math]}$ 被圆 $\text{[math]}$ 截得的弦长为6，则直线 $\text{[math]}$ 的方程为 $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024高二上·清远期末) 如图，在正方体 $\text{[math]}$ 中，点 $\text{[math]}$ 为线段 $\text{[math]}$ 上的动点，则下列结论正确的是（）

A . 当 $\text{[math]}$ 时， $\text{[math]}$ 的值最小 B . 当 $\text{[math]}$ 时， $\text{[math]}$ C . 若平面 $\text{[math]}$ 上的动点 $\text{[math]}$ 满足 $\text{[math]}$ ，则点 $\text{[math]}$ 的轨迹是椭圆 D . 直线 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角的正弦值是 $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2024高二上·清远期末) 已知双曲线 $\text{[math]}$ 的左､右焦点分别为 $\text{[math]}$ ，过点 $\text{[math]}$ 的直线与双曲线 $\text{[math]}$ 的右支交于 $\text{[math]}$ 两点， $\text{[math]}$ 与 $\text{[math]}$ 轴相交于点 $\text{[math]}$ 的内切圆与边 $\text{[math]}$ 相切于点 $\text{[math]}$ .若 $\text{[math]}$ ，则下列说法正确的有（）

A . 双曲线 $\text{[math]}$ 的渐近线方程为 $\text{[math]}$ B . 若直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 有且仅有1个公共点，则 $\text{[math]}$ C . $\text{[math]}$ 的最小值为12 D . $\text{[math]}$ 的内切圆的圆心在定直线上

答案解析收藏纠错 + 选题

三、填空题：本题共4小题，每小题5分，共20分.把答案填在答题卡的相应位置.

13. (2024高二上·清远期末) 魔方，又叫鲁比克方块，是由匈牙利布达佩斯建筑学院厄尔诺•鲁比克教授于1974年发明的机械益智玩具，与华容道､独立钻石棋同被称为智力游戏界的三大不可思议.三阶魔方（如图所示）可以看作是将一个表面涂有颜色的正方体的棱三等分，然后沿等分线把正方体切开形成27个小正方体.现将三阶魔方中1面有色的小正方体称为中心方块，2面有色的小正方体称为边缘方块，3面有色的小正方体称为边角方块，若从这27个小正方体中任取1个，则抽到的是中心方块或边角方块的概率为.

答案解析收藏纠错 + 选题
14. (2024高二上·清远期末) 设点 $\text{[math]}$ 到直线 $\text{[math]}$ 的距离为 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值是.

答案解析收藏纠错 + 选题
15. (2024高二上·清远期末) 如图，四面体 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ 的中点，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
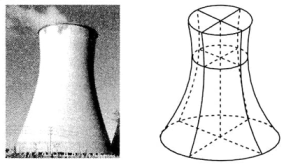
16. (2024高二上·清远期末) 如图，发电厂的冷却塔外形是由双曲线的一部分绕其虚轴所在直线旋转所得到的曲面，该冷却塔总高度为180米，水平方向上塔身最窄处的半径为30米，最高处塔口半径为 $\text{[math]}$ 米，塔底部塔口半径为 $\text{[math]}$ 米，则该双曲线的离心率为.

答案解析收藏纠错 + 选题

四、解答题：本题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤.

17. (2024高二上·清远期末) 已知数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的通项公式.
2. （2）是否存在正整数 $\text{[math]}$ 使 $\text{[math]}$ 成等比？若存在，求 $\text{[math]}$ 的值；若不存在，请说明理由.
答案解析收藏纠错 + 选题
18. (2024高二上·清远期末) 已知圆 $\text{[math]}$ 经过点 $\text{[math]}$ ，且与 $\text{[math]}$ 轴相切.
1. （1）求圆 $\text{[math]}$ 的方程；
2. （2）过点 $\text{[math]}$ 且与直线 $\text{[math]}$ 平行的光线经 $\text{[math]}$ 轴反射后与圆 $\text{[math]}$ 相交于 $\text{[math]}$ ，求 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
19. (2024高二上·清远期末) 如图，在四棱锥 $\text{[math]}$ 中，四边形 $\text{[math]}$ 是矩形， $\text{[math]}$ 为 $\text{[math]}$ 上一点，且 $\text{[math]}$ 平面 $\text{[math]}$ 到 $\text{[math]}$ 的距离为 $\text{[math]}$ .
1. （1）证明： $\text{[math]}$ .
2. （2）已知点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，且 $\text{[math]}$ ，求平面 $\text{[math]}$ 与平面 $\text{[math]}$ 夹角的余弦值.
答案解析收藏纠错 + 选题
20. (2024高二上·清远期末) 人类的四种血型与基因类型的对应为 $\text{[math]}$ 型的基因类型为 $\text{[math]}$ 型的基因类型为 $\text{[math]}$ 或 $\text{[math]}$ 型的基因类型为 $\text{[math]}$ 或 $\text{[math]}$ 型的基因类型为 $\text{[math]}$ .其中 $\text{[math]}$ 和 $\text{[math]}$ 是显性基因， $\text{[math]}$ 是隐性基因，且各基因类型是等可能的.
1. （1）若甲的父亲血型是 $\text{[math]}$ 型，母亲的血型基因类型为 $\text{[math]}$ ，求甲血型是 $\text{[math]}$ 型的概率；
2. （2）若乙的血型基因类型为 $\text{[math]}$ ，其母亲血型是 $\text{[math]}$ 型，求其父亲血型是 $\text{[math]}$ 型的概率.
答案解析收藏纠错 + 选题
21. (2024高二上·清远期末) 已知数列 $\text{[math]}$ 满足 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的通项公式；
2. （2）已知数列 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
22. (2024高二上·清远期末) 已知椭圆 $\text{[math]}$ 过 $\text{[math]}$ 两点，直线 $\text{[math]}$ 过点 $\text{[math]}$ ，且交椭圆 $\text{[math]}$ 于 $\text{[math]}$ 两点，交 $\text{[math]}$ 轴于点 $\text{[math]}$ .记 $\text{[math]}$ 的面积为 $\text{[math]}$ .
1. （1）求椭圆 $\text{[math]}$ 的标准方程.
2. （2）证明： $\text{[math]}$ 为定值.
3. （3）求 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

广东省清远市2023-2024学年高二上学期期末教学质量检测...

副标题：

*注意事项：

广东省清远市2023-2024学年高二上学期期末教学质量检测...

试题分析

总体分析

题量分析

难度分析

知识点分析

$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$