重庆市潼南区六校2023-2024学年九年级上学期数学第二次...

更新时间：2024-04-21 浏览次数：15 类型：月考试卷

一、单选题：（本大题10个小题，每小题4分，共40分）

1. (2024九下·福州开学考) -5的相反数是（）

A . 5 B . -5 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023九上·潼南月考) 如图是一个由5个相同正方体组成的立体图形，从前面看得到的图形是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023九上·潼南月考) 如图，直线 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则∠CAF的度数为（）

A . 35° B . 45° C . 55° D . 65°

答案解析收藏纠错 + 选题
4. (2023九上·潼南月考) 已知m是一元二次方程 $\text{[math]}$ 的一个根，则 $\text{[math]}$ 的值是（）

A . -2023 B . 2023 C . 2022 D . 2024

答案解析收藏纠错 + 选题
5. (2024九上·南昌月考) 抛物线 $\text{[math]}$ 的对称轴是（）

A . 直线 $\text{[math]}$ B . 直线 $\text{[math]}$ C . 直线 $\text{[math]}$ D . 直线 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024·万州模拟) 如图，每个图形都由同样大小的“△”按照一定的规律组成，其中第1个图形有5个“△”，第2个图形有10个“△”，第3个图形有15个“△”，…，则第8个图形中“△”的个数为（）

A . 40 B . 42 C . 44 D . 46

答案解析收藏纠错 + 选题
7. (2023九上·潼南月考) 估计 $\text{[math]}$ 的值应在（）

A . 3和4之间 B . 4和5之间 C . 5和6之间 D . 6和7之间

答案解析收藏纠错 + 选题
8. (2023九上·潼南月考) 如图，AB是O的直径，C为O上一点，连接AC、BC ， $\text{[math]}$ 于点E ， CD是O的切线，且 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则CD的长为（）

A . $\text{[math]}$ B . 5 C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题
9. (2023九上·潼南月考) 如图，在矩形ABCD中，以点A为圆心AD为半径顺时针旋转线段AD交AC于E ，以点C为圆心CB为半径顺时针旋转线段CB交AC于F ，连接DE、BF ，若 $\text{[math]}$ ，则∠ABF一定为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023九上·潼南月考) 学习添括号法则后，小明所在的学习小组为了加强对法则的理解，编了一个小游戏，游戏规则如下：把多项式 $\text{[math]}$ 看做a ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 五项的和，这五项可以依序循环站位，例如：当a站在第2位时， $\text{[math]}$ 站在第一位，变为多项式 $\text{[math]}$ ．在任意相邻两个或三个字母左右添括号，再在符号不变的情况下，交换括号前后两字母的位置，则称此操作为“交换操作”，例如：在b ， m两相邻字母之间先添括号得到 $\text{[math]}$ ，再交换a ， n的位置得到 $\text{[math]}$ ，下列说法：
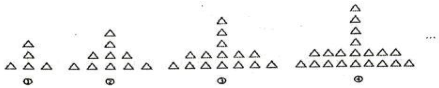
①存在一种“交换操作”后的式子与原多项式一样；
②若每次操作只在相邻两个字母变换，则这样的变换共有5种不同的结果；
③存在两个变换后多项式的差只含两个字母。
其中正确的个数是（）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题

二、填空题：（本大题8个小题，每小题4分，共32分）

11. (2023九上·潼南月考) 计算： $\text{[math]}$ 。

答案解析收藏纠错 + 选题
12. (2023九上·潼南月考) 有四张完全一样正面分别写有数字“-2”“3”“5”“7”的卡片，将其背面朝上并洗匀，从中随机抽取一张，记下卡片正面上的数字后放回，洗匀后再从中随机抽取一张，则抽取的两张卡片上的数字至少有一个是负数的概率是。

答案解析收藏纠错 + 选题
13. (2023九上·潼南月考) 一个八边形的一个外角的度数是40°，则这个八边形的与这个角不相邻的7个内角的度数和为。

答案解析收藏纠错 + 选题
14. (2023九上·潼南月考) 如图，在矩形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，作AE平分∠BAD ，若连接BF ，则BF的长度为。

答案解析收藏纠错 + 选题
15. (2023九上·潼南月考) “渝太太”“吖嘀吖嘀”等零售公司这几年在潼南迎来了蓬勃发展，其商品以价格亲民，品质较好，品种多样吸引了大量的顾客，今年4月份，潼南区江北一零售公司实现月纯利润为5万元，到6月份就突破到月纯利润为7.2万元，若该公司由4月份到6月份纯利润的月平均增长率为x ，根据题意，列出方程为。

答案解析收藏纠错 + 选题
16. (2023九上·潼南月考) 在矩形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，以A为圆心，AD为半径画弧交线段BC于E ，连接AE ，则阴影部分的面积为

答案解析收藏纠错 + 选题
17. (2023九上·潼南月考) 若关于x的不等式组 $\text{[math]}$ 有且仅有四个整数解，关于y的分式方程 $\text{[math]}$ 有整数解，则符合条件的所有整数a的和是．

答案解析收藏纠错 + 选题
18. (2023九上·潼南月考) 对于任意一个三位自然数M ，若十位数字等于百位数字与个位数字的和减2，我们称这个三位数为“减2数”．例如：640，123．最大的“减2数”是，三位数 $\text{[math]}$ 是“减2数”，记 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ 能被10整除，则满足条件的M的最大值是。

答案解析收藏纠错 + 选题

三、解答题：（本大题共8个小题，19小题8分，20-26每小题10分）

19. (2023九上·潼南月考) 计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2023九上·潼南月考) 如图， $\text{[math]}$ ， CB平分∠ABD ．
1. （1）用尺规作图完成以下基本作图：作DE平分∠BDC ，分别交AB ， BC于点E ， O ．连接CE；（保留作图痕迹，不写作法和结论．）
2. （2）根据（1）中作图，证明四边形BDCE是菱形，请你补全证明过程．证明：∵ $\text{[math]}$ ，
  ∴ $\text{[math]}$ ．
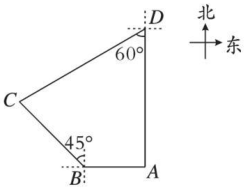
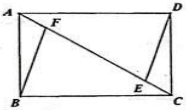
  又∵CB平分∠ABD ，
  ∴①     ▲  ，
  ∴ $\text{[math]}$ ，
  ∴②     ▲  ，
  同理： $\text{[math]}$
  ∴③     ▲  ，
  又∵ $\text{[math]}$ 即 $\text{[math]}$ ，
  ∴四边形BDCE是平行四边形．
  ∴四边形BDCE是菱形．（④             ）．
答案解析收藏纠错 + 选题
21. (2023九上·潼南月考) 某校为了加强学生对防校园欺凌的认识，组织七、八年级全体学生进行了“防校园欺凌知识”竞赛，为了解竞赛成绩，现从该校七、八年级中各随机抽取10名学生的竞赛成绩（满分100分，90分及90分以上为优秀）进行整理、描述和分析（成绩得分用x表示，共分成四组：A． $\text{[math]}$ ， B． $\text{[math]}$ ， C． $\text{[math]}$ ， D． $\text{[math]}$ ，下面给出了部分信息：
七年级抽取的10名学生的竞赛成绩是：97，82，97，86，97，96，99，100，89，82
八年级抽取的10名学生的竞赛成绩在C组中的数据是：93，94，91
七、八年级抽取的学生竞赛成绩统计表：
年级
平均数
中位数
众数
七年级
92.5
96.5
c
八年级
92.5
b
100
八年级抽取的学生竞赛成绩扇形统计图：
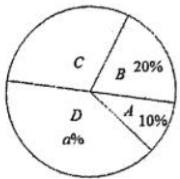
根据以上信息，解答下列问题：
1. （1）图表中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）根据以上数据，你认为该校七、八年级中哪个年级学生掌握防校园欺凌知识较好？请说明理由（一条理由即可）；
3. （3）该校七年级有520人，八年级有460人参加了此次“防校园欺凌知识”竞赛，估计参加竞赛活动成绩优秀的学生人数是多少？
答案解析收藏纠错 + 选题
22. (2023九上·潼南月考) 潼南的第一所大学---重庆电力高等专科学校第一批学生顺利入驻后，学校两旁自动形成的夜市生意也因此火爆起来，据调查，一饭店推出的两种炒饭受到了消费者的喜爱，其中“蛋炒饭”售价为15元/份，“肉丝炒饭”售价为20元/份，十月份平均每天可以卖出200份，总营业额3600元。
1. （1）求平均每天分别卖出多少份“蛋炒饭”和多少份“肉丝炒饭”？
2. （2） 11月，饭店老板为回馈消费者，对两款炒饭价格进行了下调，“蛋炒饭”的售价比十月份的价格少3元，“肉丝炒饭”的售价比国庆期间的价格降低了10%，由此，11月的第一周里，“蛋炒饭”的销量比10月平均每天增加了3m份，“肉丝炒饭”的销量比国庆期间增加了5m%，最终这两款炒饭的总营业额比10月份平均每天的总营业额减少m%，请求出m的值．
答案解析收藏纠错 + 选题
23. (2023九上·潼南月考) 如图1，△ABC是直角三角形， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点P从点B出发，以每秒1个单位长度的速度沿着 $\text{[math]}$ 方向运动到A点停止，设 $\text{[math]}$ ，点P的运动时间为x秒。
1. （1）直接写出y与x之间的函数表达式，并写出对应x的取值范围。
2. （2）在平面直角坐标系中画出y的图像，并写出y的一条性质
3. （3）结合作出的图像直接写出它与函数 $\text{[math]}$ 相交时x的值．（保留一位小数，误差不超过0.2）
答案解析收藏纠错 + 选题
24. (2023九上·潼南月考) 如图，四边形ABCD是江北云海南湾小区外公园人工湖旁的林荫小道。晚饭后，小东陪爸爸妈妈散步，从A点出发，走了200米后到达B点，再走 $\text{[math]}$ 米后到达C点，再走一段路走到了D点，小东发现：B点在A点正西方向，C点在B点西北方向，在D点南偏西60°方向，D点恰好在点A的正北方。
1. （1）求AD的长度。
2. （2）小东和小芳决定从B点同时出发来一场比赛，小东速度快，以5米每秒的平均速度沿 $\text{[math]}$ 的路线跑，小芳以4米每秒的平均速度沿 $\text{[math]}$ 的路线跑，谁先到达终点D？（参考数据： $\text{[math]}$ ； $\text{[math]}$ ）
答案解析收藏纠错 + 选题
25. (2023九上·潼南月考) 如图，抛物线 $\text{[math]}$ 与x轴交于A、B两点，点A在点B的左边，与y轴交于点C ，点A、B的坐标为 $\text{[math]}$ ， $\text{[math]}$
图1 图2
1. （1）如图1，求抛物线的解析式；
2. （2）如图1，点D在直线BC上方的抛物线上运动（不含端点B、C），连接DC、DB ，当△BCD面积最大时，求出面积最大值和点D的坐标；
3. （3）如图2，将（1）中的抛物线向右平移，当它恰好经过原点时，设原抛物线与平移后的抛物线交于点E ，连接BE ．点M为原抛物线对称轴上一点，以B、E、M为顶点的三角形是直角三角形时，写出所有符合条件的点M的坐标，并写出求解点M的坐标的其中一种情况．
答案解析收藏纠错 + 选题
26. (2023九上·潼南月考) 如图，在Rt△ABC中， $\text{[math]}$ ， $\text{[math]}$ ，点E是CA延长线上一点，连接BE ，点D是AB边，上一动点，且 $\text{[math]}$ ，过点D作 $\text{[math]}$ ，垂足为点F ．
图1 图2图3
1. （1）如图1，若 $\text{[math]}$ ， $\text{[math]}$ ，求CF的长；
2. （2）如图2，连接AF ，求证： $\text{[math]}$ ；
3. （3）如图3，过点A作 $\text{[math]}$ ，连接BM并延长交AC于点N ，若 $\text{[math]}$ ，当BM最小时，直接写出△ACM的面积．
答案解析收藏纠错 + 选题