江西省南昌市西湖区立德朝阳中学2023-2024学年九年级上...

更新时间：2024-12-23 浏览次数：6 类型：期中考试

一、单项选择题。（本大题共6小题，每小题3分，共18分）在每小题列出的四个备选项中只有一项是最符合题目要求的，请将其代码填涂在答题卡相应位置.错选、多选或未选均不得分。

1. (2023九上·西湖期中) 在如图所示标志中，既是轴对称图形，又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023九上·西湖期中) 不透明的袋子中只有4个黑球和2个白球，这些球除颜色外无其他差别，随机从袋子中一次摸出3个球，下列事件是不可能事件的是（　　）

A . 3个球都是黑球 B . 3个球都是白球 C . 3个球中有黑球 D . 3个球中有白球

答案解析收藏纠错 + 选题
3. (2023九上·西湖期中) 如图，∠DCE是⊙O内接四边形ABCD的一个外角，若∠DCE＝82°，那么∠BOD的度数为（　　）

A . 160° B . 162° C . 164° D . 170°

答案解析收藏纠错 + 选题
4. (2024九下·张北开学考) 小明将图案绕某点连续旋转若干次，每次旋转相同角度 $\text{[math]}$ ，设计出一个外轮廓为正六边形的图案（如图），则 $\text{[math]}$ 可以为（）

A . 30° B . 60° C . 90° D . 120°

答案解析收藏纠错 + 选题
5. (2023九上·西湖期中) 如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝1，将△ABC绕点C顺时针旋转60°得到△A'B'C，其中点A'与点A是对应点，点B'与点B是对应点．若点B'恰好落在AB边上，则点A到直线A'C的距离等于（　　）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023九上·西湖期中) 斐波那契数列指的是这样一列数：1，1，2，3，5，8，…（从第3个数起，每个数是前面两数的和）．如图，用以这些数为边长的正方形拼成长方形，在以这些数为边长的正方形中作出圆心角为90°的圆弧，则接下来一段圆弧对应的扇形面积是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题。（本大题共6小题，每小题3分，共18分）

7. (2023九上·西湖期中) 若点P（m ， 1）关于原点的对称点Q（﹣2，n），那么m+n＝．

答案解析收藏纠错 + 选题
8. (2023九上·西湖期中) 将含有30°角的直角三角板OAB如图所示放置在平面直角坐标系中，OB在x轴上，若 $\text{[math]}$ ，将三角板绕原点O顺时针旋转90°，则点A的对应点A^'的坐标为．

答案解析收藏纠错 + 选题
9. (2023九上·西湖期中) 若一个扇形的半径是18cm，且它的弧长是 $\text{[math]}$ ，则此扇形的圆心角等于．

答案解析收藏纠错 + 选题
10. (2023九上·西湖期中) 如图，把Rt△ABC绕点A逆时针旋转44°，得到Rt△AB'C'，点C'恰好落在边AB上，连接BB'，则∠BB'C'＝度．

答案解析收藏纠错 + 选题
11. (2023九上·西湖期中) 如图，正方形ABCD内接于⊙O，⊙I是△ABC的内切圆，则⊙O的半径与⊙I的半径的比值是．

答案解析收藏纠错 + 选题
12. (2023九上·西湖期中) 如图，已知△ABC为等腰直角三角形，∠BAC＝90°，AC＝2，以点C为圆心，1为半径作圆，点P为⊙C上一动点，连接AP，并绕点A顺时针旋转90°得到AP^' ，连接CP^' ，则CP^'的取值范围是．

答案解析收藏纠错 + 选题

三、解答题。（本大题共5小题，每小题6分，共30分）

13. (2023九上·西湖期中)
1. （1）一个口袋中有3个黑球和若干个白球，在不允许将球倒出来的前提下，小明为估计其中的白球数，采用了如下的方法：从口袋中随机摸出一个球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色，…，不断重复上述过程，小明共摸了100次，其中20次摸到黑球根据上述数据，估计口袋中的白球大约有多少个？
2. （2）如图，P是正方形ABCD内一点，△ABP绕着点B旋转后能到达△CBE的位置．若BP＝3cm，求线段PE的长．
答案解析收藏纠错 + 选题
14. (2023九上·西湖期中) HUAWEIMate60Pro于8月29日上市，该系列完成了核心技术领域从0到1的跃迁，让无数国人为之自豪并被赞誉为“争气机”．手机背面有一条圆弧，象征着以山河之美致敬奔腾不息的力量．圆弧对应的弦AB长80mm，弓形高CD长14mm求半径OA的长．

答案解析收藏纠错 + 选题
15. (2023九上·西湖期中) 创新作图
如图是由小正方形构成的7×7网格，每个小正方形的顶点叫做格点．⊙O经过A、B、C三个格点，连接AB，AC，BC，仅用无刻度直尺在给定网格中按要求画图．（不写作法）
1. （1）在圆上找点D，使得∠BAD＝90°；
2. （2）在劣弧BC上找点D，使得∠CBD＝45°．
答案解析收藏纠错 + 选题
16. (2023九上·西湖期中) 家庭成员尤其是父母对待日常生活和工作的态度和处事方法都会对孩子有潜移默化的影响，父母在教育孩子认识问题和解决问题方面对孩子采取怎样的指导、帮助、要求，都会形成孩子对待问题的方式．为此，某校举行了一次“智慧家长”系列讲座活动，活动过程中，甲、乙、丙、丁四位家长踊跃发言，积极互动．活动后校方准备从这四位家长中随机抽选一位作为家长代表做总结发言，并从剩下的三位家长中随机抽选一位做进一步访谈调查．
1. （1）选择家长乙作为家长代表做总结发言的概率为；
2. （2）请用列表法或画树状图的方法求家长甲作为家长代表做总结发言，且家长丁被抽选做进一步访谈调查的概率．
答案解析收藏纠错 + 选题
17. (2023九上·西湖期中) 如图1中的某种冰激凌的外包装可以视为圆锥（如图2），制作这种外包装需要用如图3所示的等腰三角形材料，其中AB＝AC ， AD⊥BC将扇形EAF围成圆锥时，AE、AF恰好重合，已知这种加工材料的顶角∠BAC＝90°．
1. （1）求图2中圆锥底面圆直径ED与母线AD长的比值；
2. （2）若圆锥底面圆的直径ED为5cm ，求加工材料剩余部分（图3中阴影部分）的面积．（结果保留π）
答案解析收藏纠错 + 选题

四、解答题。（本大题共3小题，每小题8分，共24分）

18. (2023九上·西湖期中) 某超市设计的“春节大酬宾”促销活动如下：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”“20元”“20元”和“40元”的字样，规定：在本超市同一日内，顾客每消费满200元，就可以在箱子里先后摸出两个球（第一次摸出后不放回）．超市根据两个小球所标金额的和直接进行减价优惠，李叔叔刚好消费200元．
1. （1）从箱子里任意摸出一个球，摸到球上标有“50元”字样的球是事件；摸到球上标有“0元”字样的球是事件；（均填“不可能”“必然”或“随机”）
2. （2）求出李叔叔所获得的优惠金额大于50元的概率．（列表或画树状图求解）
答案解析收藏纠错 + 选题
19. (2023九上·西湖期中) 如图1，重庆特色的九宫格火锅分九格：四角格、十字格、中心格（中心格一般为正方形）．隔板的设计有以下两种：①横纵隔板两两垂直交于隔板的三等分点如图2所示；②横纵隔板两两垂直交于圆锅边缘（圆）八等分点如图3所示．已知圆锅直径为40cm．
1. （1）求图2的中心格面S₁；
2. （2）求两种设计的中心格面积S₁与S₂差．
答案解析收藏纠错 + 选题
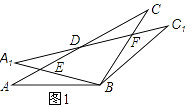
20. (2023九上·西湖期中) 在△ABC中，AB=BC=2，∠ABC=120°，将△ABC绕点B顺时针旋转角α（0°＜α＜90°）得△A₁BC₁ ， A₁B交AC于点E，A₁C₁分别交AC、BC于D、F两点．
1. （1）如图1，观察并猜想，在旋转过程中，线段BE与BF有怎样的数量关系？并证明你的结论；
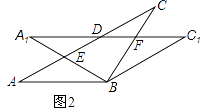
2. （2）如图2，当α=30°时，试判断四边形BC₁DA的形状，并说明理由．
答案解析收藏纠错 + 选题

五、解答题。（本大题共2小题，每小题9分，共18分）

21. (2023九上·西湖期中) 如图，在平面直角坐标系中，AB∥OC，A（0， $\text{[math]}$ ）、C（﹣4，0），且 AB＝2．以BC为直径作⊙O₁交OC于点D，过点D作直线DE交线段OA于点E，且∠EDO＝30°
1. （1）求证：DE是⊙O₁的切线；
2. （2）若线段BC上存在一点P，使以点P为圆心，PC为半径的⊙P与y轴相切，求点P的坐标．
答案解析收藏纠错 + 选题
22. (2023九上·西湖期中) 如图，在△ABC中，∠BAC＝90°，AB＝AC，D为BC的中点，点E为平面内一点，连接DE，将DE绕点D顺时针旋转90°，点E的对应点为F，连接EF，AE，CF．
1. （1）如图1，当点E在边AC上时，请直接写出线段AE，CF之间的数量关系，位置关系；
2. （2）如图2，当点E在△ABC内部时，判断（1）中结论是否依然成立，并说明理由；
3. （3） AE＝5，DE＝3，若A，E，F三点共线，请直接写出线段BE的值．
答案解析收藏纠错 + 选题

六、解答题。（本大题共12分）

23. (2023九上·西湖期中)
1. （1）【教材呈现】以下是人教版八年级下册数学教材第50页的部分内容．如图，直线l₁∥l₂ ， △ABC与△DBC的面积相等吗？为什么？
2. （2）【基础巩固】如图1，正方形ABCD内接于⊙O，直径MN∥AD，求阴影面积与圆面积的比值；
3. （3）【尝试应用】如图2，在半径为5的⊙O中，BD＝CD，∠ACO＝2∠BDO，AB＝4，求S_△_ABC；
4. （4）【拓展提高】如图3，AB是⊙O的直径，点P是OB上一点，过点P作弦CD⊥AB于点P，点F是⊙O上的点，且满足CF＝CB，连接BF交CD于点E，若BF＝8EP， $\text{[math]}$ ，求⊙O的半径．
答案解析收藏纠错 + 选题