浙江省舟山市定海区金衢山五校联考2023-2024学年九年级...

更新时间：2024-04-03 浏览次数：31 类型：开学考试

一、选择题（本题有10小题，每题3分，共30分．请选出各题中唯一的正确选项，不选、多选、错选，均不得分）

1. (2024九上·鄞州月考) 二次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ，则a的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
2. (2024九下·定海开学考) 一个不透明的盒子内装有1个红球，1个黄球，1个蓝球，它们除颜色外其余均相同．现从中随机摸出一球，记下颜色后放回搅匀，如此继续．小州摸球两次，则出现相同颜色的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九下·定海开学考) 如图，正六边形 $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ 的半径为6，则这个正六边形的边心距 $\text{[math]}$ 和弧 $\text{[math]}$ 的长分别为（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九下·定海开学考) “圆”是中国文化的一个重要精神元素，在中式建筑中有着广泛的应用，例如古典园林中的门洞如图1，其数学模型为如图2所示．园林中的一个圆弧形门洞的地面跨径 $\text{[math]}$ 米，D为圆上一点， $\text{[math]}$ 于点C，且 $\text{[math]}$ 米，则门洞的半径为（）

A . $\text{[math]}$ 米 B . $\text{[math]}$ 米 C . $\text{[math]}$ 米 D . $\text{[math]}$ 米

答案解析收藏纠错 + 选题
5. (2024九下·定海开学考) 如图， $\text{[math]}$ 中， $\text{[math]}$ 于点 $\text{[math]}$ ，点 $\text{[math]}$ 为线段 $\text{[math]}$ ， $\text{[math]}$ 上两点，满足 $\text{[math]}$ ，则 $\text{[math]}$ 的比值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九上·市中区期中) 若 $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九下·定海开学考) 如图，在矩形ABCD中，点 $\text{[math]}$ 是边BC的三等分点 $\text{[math]}$ ，点 $\text{[math]}$ 是边CD的中点，线段AG，AH与对角线BD分别交于点E，F．设矩形ABCD的面积为 $\text{[math]}$ ，则以下4个结论中：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ．正确的结论有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
8. (2024九下·定海开学考) 如图， $\text{[math]}$ 的直角顶点在坐标原点 $\text{[math]}$ 上，点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024九下·定海开学考) 如图， $\text{[math]}$ 的内接正六边形 $\text{[math]}$ ，以 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径作弧 $\text{[math]}$ ，以 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径作弧 $\text{[math]}$ ，已知 $\text{[math]}$ 的半径为2，则边 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 围成的阴影部分面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024九下·定海开学考) 如图，在平面直角坐标系 $\text{[math]}$ 中，点A坐标为 $\text{[math]}$ ，点B坐标为 $\text{[math]}$ ， $\text{[math]}$ 的半径为4（O为坐标原点），点C是 $\text{[math]}$ 上一动点，过点B作直线 $\text{[math]}$ 的垂线 $\text{[math]}$ ， P为垂足，点C在 $\text{[math]}$ 上运动一周，则点P运动的路径长等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本题有6小题，每题4分，共24分）

11. (2024九下·定海开学考) 已知 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
12. 某种麦粒在相同条件下进行发芽试验，结果如下表所示：
试验的麦粒数 $\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
发芽的麦粒数 $\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
发芽的频率 $\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
则任取一粒麦粒，估计它能发芽的概率约为．（结果精确到 $\text{[math]}$ ）

答案解析收藏纠错 + 选题
13. (2024九下·定海开学考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，分别以各边为直径作半圆，图中阴影部分在数学史上称为“希波克拉底月牙”，若 $\text{[math]}$ ， $\text{[math]}$ ，则图中阴影部分的面积为．

答案解析收藏纠错 + 选题
14. (2024九下·定海开学考) 燕尾夹是我们平时学习、工作中经常用到的工具之一，一种燕尾夹如图 $\text{[math]}$ 所示，图 $\text{[math]}$ 是在打开状态时的示意图，图 $\text{[math]}$ 是在闭合状态时的示意图（数据如图，单位： $\text{[math]}$ ），则从打开到闭合， $\text{[math]}$ 之间的距离增加了 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2024九下·定海开学考) 如图， $\text{[math]}$ 为 $\text{[math]}$ 的直径， $\text{[math]}$ 为半圆上一点且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别为 $\text{[math]}$ ， $\text{[math]}$ 的中点，弦 $\text{[math]}$ 分别交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2024九下·定海开学考) 如图所示， $\text{[math]}$ ，半径为2的圆O内切于 $\text{[math]}$ .P为圆O上一动点，过点P作 $\text{[math]}$ 、 $\text{[math]}$ 分别垂直于 $\text{[math]}$ 的两边，垂足为M、N，则 $\text{[math]}$ 的取值范围为 .

答案解析收藏纠错 + 选题

三、解答题（本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）

17. (2023九上·振兴联盟期末) 计算：
1. （1） $\text{[math]}$ ；
2. （2）已知线段 $\text{[math]}$ ， $\text{[math]}$ ，线段c是线段 $\text{[math]}$ ， $\text{[math]}$ 的比例中项，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
18. (2024九下·定海开学考) $\text{[math]}$ 在平面直角坐标系中的位置如图所示：
1. （1）画出 $\text{[math]}$ 关于原点对称的 $\text{[math]}$ ；
2. （2）将 $\text{[math]}$ 绕点C顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，画出旋转后的 $\text{[math]}$ ．并求出 $\text{[math]}$ 、 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
19. (2024九下·定海开学考) $\text{[math]}$ 年杭州亚运会球类比赛中，有 $\text{[math]}$ 排球， $\text{[math]}$ 篮球， $\text{[math]}$ 足球， $\text{[math]}$ 羽毛球， $\text{[math]}$ 乒乓球五种比赛很受我校同学们喜爱．小海同学随机对我校同学在亚运会期间最想观看的一种球类比赛做了一次随机调査统计，并根据这个统计结果制作了如下两幅不完整的统计图：
1. （1）请补全条形统计图；
2. （2）若我校学生约有 $\text{[math]}$ 人，试估计想观看 $\text{[math]}$ 种比赛的学生约有人．
3. （3）小海同学在 $\text{[math]}$ 月 $\text{[math]}$ 号到杭州观看亚运会比赛，发现当天有比赛的是 $\text{[math]}$ 四种比赛，若从中任选两种比赛观看，求选到 $\text{[math]}$ 两种比赛的概率．（要求画树状图或列表求概率）
答案解析收藏纠错 + 选题
20. (2024九上·红塔期末) 如图，在 $\text{[math]}$ 中，弦 $\text{[math]}$ 和半径 $\text{[math]}$ 相交于点 $\text{[math]}$ 与 $\text{[math]}$ 互相平分，连接 $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是菱形；
2. （2）若扇形 $\text{[math]}$ （图中阴影部分）的面积为 $\text{[math]}$ ，求 $\text{[math]}$ 与 $\text{[math]}$ 间的距离．
答案解析收藏纠错 + 选题
21. (2024九下·定海开学考) 如图1，一个移动喷灌架喷射出的水流可以近似地看成抛物线．图2是喷灌架为一坡地草坪喷水的平面示意图，喷水头的高度(喷水头距喷灌架底部的距离)是1米，当喷射出的水流与喷灌架的水平距离为10米时，达到最大高度6米，现将喷灌架置于坡地底部点O处，草坡上距离O的水平距离为15 米处有一棵高度为1.2米的小树AB，AB垂直水平地面且A点到水平地面的距离为3米．
1. （1）计算说明小树是否会对水流浇灌到树后面的草坪造成影响?
2. （2）求水流的高度与斜坡铅垂高度差的最大值．
答案解析收藏纠错 + 选题

22. (2024九下·定海开学考) 仁皇阁是一个著名景点，某校九年级研学期间参观了仁皇阁，数学兴趣小组对仁皇阁高度产生了浓厚的兴趣，他们想运用所学知识估算出仁皇阁的高度。

课题	估算仁皇阁高度
测量工具	测量角度的仪器，皮尺，刻度尺等
组别	测量方案示意图	测量方案说明
组1		如图1 ，先在仁皇阁底部广场的C处用仪器测得阁楼顶端A的仰角为27° ，然后从C处向阁楼底部前进10m到达D处，此时在D处测得阁楼顶端A的仰角为30° ．
组2		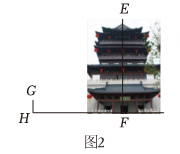如图2 ，身高1.5m的组员站在仁皇阁正门边上合影．打印出照片后量得此组员图上高度GH为0.5cm，量得仁皇阁图上高度EF为12.9cm.

（1）任务一请分别计算两组中测量得到的阁楼高度；（结果保留小数点后一位．参考数据 $\text{[math]}$ ）
（2）任务二后续经过查证后发现小组2数据更为精确，请你帮小组1分析可能产生误差的原因．（写出一条即可）

答案解析收藏纠错 + 选题

23. (2024九下·定海开学考) 【问题背景】综合实践活动课上，老师给每个小组准备了一张边长为 $\text{[math]}$ 的正方形硬纸板，要求用该硬纸板制作一个无盖的纸盒．怎样制作能使无盖纸盒的容积最大呢？
【建立模型】如图1，小海所在小组从四个角各剪去一个边长为 $\text{[math]}$ 的小正方形，再折成如图2所示的无盖纸盒，记它的容积为 $\text{[math]}$ ．
1. （1）任务1 请你写出 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式．
2. （2）【探究模型】为了直观反映无盖纸盒的容积 $\text{[math]}$ 随 $\text{[math]}$ 的变化规律，小海类比函数的学习进行了如下探究．
  任务2 ①列表：请你补充表格中的数据．
  $\text{[math]}$
  0
  2.5
  5
  7.5
  10
  12.5
  15
  $\text{[math]}$
  0
  1562.5
  
  1687.5
  
  312.5
  0
  ②描点：把上表中各组对应值作为点的坐标，在平面直角坐标系中描出相应的点．
  ③连线：用光滑的曲线按自变量从小到大的顺次连结各点．
3. （3）【解决问题】画完函数的图象后，小海所在的小组发现，在一定范围内 $\text{[math]}$ 随 $\text{[math]}$ 的增大而增大，在一定范围内 $\text{[math]}$ 随 $\text{[math]}$ 的增大而减小．
  任务3 利用函数图象回答：当 $\text{[math]}$ 为何值时，小海所在小组设计的无盖纸盒的容积最大？最大值为多少？
答案解析收藏纠错 + 选题
24. (2024九下·定海开学考) 在菱形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是射线 $\text{[math]}$ 上一动点，以 $\text{[math]}$ 为一边向右侧作等腰 $\text{[math]}$ ，使 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 的位置随着点 $\text{[math]}$ 的位置变化而变化．
1. （1）如图 $\text{[math]}$ ，若 $\text{[math]}$ ，当点 $\text{[math]}$ 在菱形 $\text{[math]}$ 内时，连接 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是， $\text{[math]}$ 与 $\text{[math]}$ 的位置关系是；
2. （2）若 $\text{[math]}$ ，当点 $\text{[math]}$ 在线段 $\text{[math]}$ 的延长线上时，
  ①如图 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 有何数量关系， $\text{[math]}$ 与 $\text{[math]}$ 有何位置关系？请说明理由；
  ②如图 $\text{[math]}$ ，连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，求线段 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙江省舟山市定海区金衢山五校联考2023-2024学年九年级...

副标题：

*注意事项：

浙江省舟山市定海区金衢山五校联考2023-2024学年九年级...

试题分析

总体分析

题量分析

难度分析

知识点分析

试验的麦粒数 $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
发芽的麦粒数 $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
发芽的频率 $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

$\text{[math]}$	0	2.5	5	7.5	10	12.5	15
$\text{[math]}$	0	1562.5		1687.5		312.5	0