四川省成都市武侯区成都西川中学2023-2024学年九年级上...

更新时间：2024-04-26 浏览次数：20 类型：期末考试

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡上）

1. (2024九上·武侯期末) 方程 $\text{[math]}$ 的二次项系数、一次项系数和常数项分别是（）

A . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九上·武侯期末) 如图所示的几何体的左视图是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024九上·岳阳月考) 已知 $\text{[math]}$ ，则下列式子一定正确的是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九上·武侯期末) 如图，在平面直角坐标系中， $\text{[math]}$ 与 $\text{[math]}$ 关于原点O位似，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 为（　　）

A . 2 B . 4 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九上·武侯期末) 关于反比例函数 $\text{[math]}$ 的图象性质，下列说法正确的是（）

A . 图象经过点 $\text{[math]}$ B . 图象位于第二、四象限 C . 当 $\text{[math]}$ 时，y随x的增大而增大 D . 当 $\text{[math]}$ 时， $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九上·武侯期末) 如图，点E是线段BC的中点， $\text{[math]}$ ，下列结论中，说法错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九上·武侯期末) 如图，某小区居民休闲娱乐中心是一块长方形（长60米，宽40米）场地，被3条宽度相同的绿化带分为总面积为1750平方米的活动场所，如果设绿化带的宽度为x米，由题意可列方程为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. 如图，在正方形ABCD中，点E在边AB上，以DE为边作矩形DEFG ，使FG经过点C ，若AD＝2，则矩形DEFG的面积是（）

A . 2 B . 4 C . 2 $\text{[math]}$ D . 4 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上）

9. (2024九上·武侯期末) 如图，平行四边形 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 延长线上一点， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
10. (2024九上·武侯期末) 已知 $\text{[math]}$ ， $\text{[math]}$ 都在反比例函数 $\text{[math]}$ 的图象上，且 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 大小关系是．

答案解析收藏纠错 + 选题
11. (2024九上·武侯期末) 如图，在一个改良版的飞镖盘 $\text{[math]}$ 中， $\text{[math]}$ 是线段 $\text{[math]}$ 上的两个黄金分割点，连接 $\text{[math]}$ ．现向 $\text{[math]}$ 区域内随机投掷一枚飞镖，投中阴影部分的概率是．

答案解析收藏纠错 + 选题
12. (2024九上·乌鲁木齐月考) 已知方程 $\text{[math]}$ 的根为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
13. (2024九上·武侯期末) 如图，矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，以点B为圆心，适当长为半径画弧，分别交 $\text{[math]}$ ， $\text{[math]}$ 于点E ， F ，再分别以点E ， F为圆心，大于 $\text{[math]}$ 长为半径画弧交于点P作射线 $\text{[math]}$ ，过点C作 $\text{[math]}$ 的垂线分别交 $\text{[math]}$ ， $\text{[math]}$ 于点M ， N ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题

三、解答题（本大题共5个小题，共48分，答案写在答题卡上）

14. (2024九上·武侯期末)
1. （1）解方程 $\text{[math]}$ ；
2. （2）解方程 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
15. (2024九上·武侯期末) 小明想利用太阳光测量楼高．他带着皮尺来到一栋楼下，发现对面墙上有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：
如示意图，小明边移动边观察，发现站到点 $\text{[math]}$ 处时，可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠，且高度恰好相同．此时，测得小明落在墙上的影子高度 $\text{[math]}$ m， $\text{[math]}$ m， $\text{[math]}$ m（点 $\text{[math]}$ 在同一直线上）．
已知小明的身高 $\text{[math]}$ 是1.7m，请你帮小明求出楼高 $\text{[math]}$ （结果精确到0.1m）．

答案解析收藏纠错 + 选题
16. (2024九上·武侯期末) 有4张相同的卡片上分别写有数字0、1、 $\text{[math]}$ 、3，将卡片的背面朝上，洗匀后从中任意抽取1张，将卡片上的数字记录下来；再从余下的3张卡片中任意抽取1张，同样将卡片上的数字记录下来．
1. （1）第一次抽取的卡片上数字是非负数的概率
2. （2）小敏设计了如下游戏规则：当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时，甲获胜；否则，乙获胜，小敏设计的游戏规则公平吗？为什么？（请用树状图或列表等方法说明理由）
答案解析收藏纠错 + 选题
17. (2024九上·武侯期末) 如图，在 $\text{[math]}$ 中，E为边 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ， $\text{[math]}$ ，交于点F ，且 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 和 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
18. (2024九上·武侯期末) 如图，反比例函数 $\text{[math]}$ 与一次函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ，点 $\text{[math]}$ ，一次函数 $\text{[math]}$ 与y轴交于点C．
1. （1）求反比例函数和一次函数解析式；
2. （2）连接 $\text{[math]}$ ，求 $\text{[math]}$ 的面积；
3. （3）如图2，点E是反比例函数图象上A点右侧一点，连接 $\text{[math]}$ ，把线段 $\text{[math]}$ 绕点A顺时针旋转 $\text{[math]}$ ，点E的对应点F恰好也落在这个反比例函数的图象上，求点E的坐标．
答案解析收藏纠错 + 选题

四、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上）

19. (2024九上·武侯期末) 若 $\text{[math]}$ ， $\text{[math]}$ 是一元二次方程 $\text{[math]}$ 的两个实数根，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
20. (2024九上·武侯期末) 定义：如果三角形的一个内角是另一个内角的2倍，那么称这个三角形为倍角三角形．若在一个倍角三角形 $\text{[math]}$ 中， $\text{[math]}$ ，则其最小的内角度数为．

答案解析收藏纠错 + 选题
21. (2024九上·武侯期末) 如图，将 $\text{[math]}$ 沿 $\text{[math]}$ 边上的中线 $\text{[math]}$ 平移到 $\text{[math]}$ 的位置，已知 $\text{[math]}$ 的面积为 $\text{[math]}$ ，阴影部分三角形的面积为 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
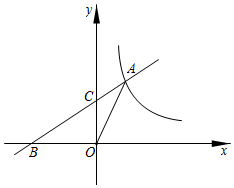
22. (2024九上·武侯期末) 如图，点A在反比例函数y＝ $\text{[math]}$ （x＞0）的图象上，点B在x轴负半轴上，直线AB交y轴于点C，若 $\text{[math]}$ ＝ $\text{[math]}$ ，△AOB的面积为6，则k的值为.

答案解析收藏纠错 + 选题
23. (2024九上·武侯期末) 如图，直角坐标系中，正方形 $\text{[math]}$ 的顶点A与原点O重合，点B在x轴的正半轴上，点D在y轴的正半轴上，在边 $\text{[math]}$ 的上侧作等腰三角形 $\text{[math]}$ ，使 $\text{[math]}$ ，连接AE ，过点D作 $\text{[math]}$ 的垂线，垂足为G ，交 $\text{[math]}$ 的延长线于点F ，连接 $\text{[math]}$ ．若点D的坐标为 $\text{[math]}$ ， $\text{[math]}$ 的长度为2，则点E的坐标为．

答案解析收藏纠错 + 选题

五、解答题（本大题共3个小题，共30分，答案写在答题卡上）

24. (2024九上·武侯期末) 某超市经销一种商品，每千克成本为30元，经试销发现，该种商品的每天销售量y（千克）与销售单价x（元/千克）满足一次函数关系，其每天销售单价，销售量的四组对应值如表所示：
销售单价x（元/千克）
40
45
55
60
销售量y（千克）
80
70
50
40
1. （1）求y（千克）与x（元/千克）之间的函数表达式；
2. （2）若商店按销售单价不低于成本价，且不高于60元的价格销售，要使销售该商品每天获得的利润为800元，则每天的销售单价应为每千克多少元？
答案解析收藏纠错 + 选题
25. (2024九上·武侯期末) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点E是 $\text{[math]}$ 边上一点，连接 $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠得到 $\text{[math]}$ ，边 $\text{[math]}$ ， $\text{[math]}$ 分别交 $\text{[math]}$ 于点M ， N ．
1. （1）求证： $\text{[math]}$ ；
2. （2）当 $\text{[math]}$ 时．
  ①求BE的长；
  ②若点P是 $\text{[math]}$ 边上的动点，连接 $\text{[math]}$ ，过点A作 $\text{[math]}$ 的垂线交线段 $\text{[math]}$ 于点Q ，试探究 $\text{[math]}$ 的值是否发生变化，若变化，请说明理由；若不变，请求出 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
26. (2024九上·武侯期末) 如图，在平面直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 分别交 $\text{[math]}$ 轴、 $\text{[math]}$ 轴于点 $\text{[math]}$ ， B ， $\text{[math]}$ ，过点 $\text{[math]}$ 的直线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ 是线段 $\text{[math]}$ 上一点（不与 $\text{[math]}$ 重合）．
1. （1）求直线 $\text{[math]}$ 的解析式及点 $\text{[math]}$ 的坐标；
2. （2）点 $\text{[math]}$ 是平面内一点，若以 $\text{[math]}$ 为顶点的四边形是菱形，直接写出点 $\text{[math]}$ 的坐标；
3. （3）作 $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ 于 $\text{[math]}$ ，连接 $\text{[math]}$ ．
  ①若 $\text{[math]}$ 与 $\text{[math]}$ 相似，求点 $\text{[math]}$ 的坐标；
  ②取 $\text{[math]}$ 的中点 $\text{[math]}$ ，直接写出 $\text{[math]}$ 周长的最小值．
答案解析收藏纠错 + 选题