备考2024年中考数学探究性训练专题24 图形的平移

更新时间：2024-03-31 浏览次数：29 类型：二轮复习

一、理论探究题

1. (2023·吉林)
1. （1）【操作发现】如图①，剪两张对边平行的纸条，随意交叉叠放在一起，使重合的部分构成一个四边形 $\text{[math]}$ ．转动其中一张纸条，发现四边形 $\text{[math]}$ 总是平行四边形其中判定的依据是．
2. （2）【探究提升】取两张短边长度相等的平行四边形纸条 $\text{[math]}$ 和 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ），其中 $\text{[math]}$ ， $\text{[math]}$ ，将它们按图②放置， $\text{[math]}$ 落在边 $\text{[math]}$ 上， $\text{[math]}$ 与边 $\text{[math]}$ 分别交于点M，N．求证： $\text{[math]}$ 是菱形．
3. （3）【结论应用】保持图②中的平行四边形纸条 $\text{[math]}$ 不动，将平行四边形纸条 $\text{[math]}$ 沿 $\text{[math]}$ 或 $\text{[math]}$ 平移，且 $\text{[math]}$ 始终在边 $\text{[math]}$ 上．当 $\text{[math]}$ 时，延长 $\text{[math]}$ 交于点P，得到图③．若四边形 $\text{[math]}$ 的周长为40， $\text{[math]}$ （ $\text{[math]}$ 为锐角），则四边形 $\text{[math]}$ 的面积为．
答案解析收藏纠错 + 选题
2. (2022·临沭模拟) 综合与实践
【问题背景】

如图1，矩形 $\text{[math]}$ 中， $\text{[math]}$ .点E为边 $\text{[math]}$ 上一点，沿直线 $\text{[math]}$ 将矩形折叠，使点C落在 $\text{[math]}$ 边的点 $\text{[math]}$ 处.
1. （1）【问题解决】
  填空： $\text{[math]}$ 的长为.
2. （2）如图2，将 $\text{[math]}$ 沿线段 $\text{[math]}$ 向右平移，使点 $\text{[math]}$ 与点B重合，得到 $\text{[math]}$ 与 $\text{[math]}$ 交于点F， $\text{[math]}$ 与 $\text{[math]}$ 交于点G.求 $\text{[math]}$ 的长；
3. （3）【拓展探究】
  在图2中，连接 $\text{[math]}$ ，则四边形 $\text{[math]}$ 是平行四边形吗？若是，请予以证明；若不是，请说明理由.
答案解析收藏纠错 + 选题
3. (2024八上·长春净月高新技术产业开发期末)
1. （1）【问题背景】教材阅读材料告诉我们，全等三角形的三个基本事实是进行演绎推理的重要依据．它们是从静态的角度探索发现的判定方法，其本质与动态的全等三角形定义是一致的，即在这些条件下，两个三角形一定可以通过图形的基本变换（轴对称、平移与旋转）而相互重合．
  利用动态的全等三角形定义，上图中的两个三角形可以看作通过轴对称变换得到的全等的是，可以看作通过平移变换得到的全等的是，可以看作通过旋转变换得到的全等的是．（填序号即可）
2. （2）【问题呈现】在 $\text{[math]}$ 中， $\text{[math]}$ 为边 $\text{[math]}$ 上一点（不与 $\text{[math]}$ 重合），连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 延长线于点 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 中点，连接 $\text{[math]}$ ．
  
  求证： $\text{[math]}$ ；
3. （3）若将（1）中两个全等三角形看作动态变化的两个三角形，那么其中一个三角形可以看作是由另一个三角形通过图形的基本变换而相互重合（填：“轴对称”、“平移”或“旋转”），简述变换的主要过程（包含变换的基本要素）；
4. （4）直接写出 $\text{[math]}$ 和 $\text{[math]}$ 之间的数量关系．
答案解析收藏纠错 + 选题
4. (2023八下·通川期末) 在一次数学研究性学习中，小兵将两个全等的直角三角形纸片ABC和DEF拼在一起，使点A与点F重合，点C与点D重合（如图1），其中∠ACB＝∠DFE＝90°，BC＝EF＝3cm，AC＝DF＝4cm，并进行如下研究活动．

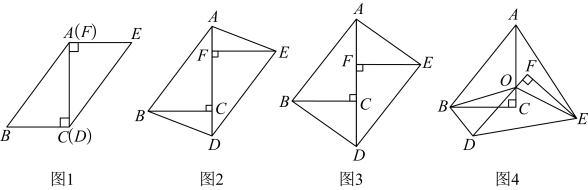
活动一：将图1中的纸片DEF沿AC方向平移，连结AE，BD（如图2），当点F与点C重合时停止平移．
1. （1）【思考】图2中的四边形ABDE是平行四边形吗？请说明理由．
2. （2）【发现】当纸片DEF平移到某一位置时，小兵发现四边形ABDE为矩形（如图3）．求AF的长．
3. （3）活动二：在图3中，取AD的中点O，再将纸片DEF绕点O顺时针方向旋转α度（0≤α≤90），连结OB，OE（如图4）．
  【探究】当EF平分∠AEO时，探究OF与BD的数量关系，并说明理由．
答案解析收藏纠错 + 选题
5. (2022八下·晋中期末) 综合与探究：如图，在平面直角坐标系 $\text{[math]}$ 中，四边形 $\text{[math]}$ 是平行四边形， $\text{[math]}$ ， $\text{[math]}$ 两点的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ．将 $\text{[math]}$ 先向右平移4个单位后，再向下平移 $\text{[math]}$ 个单位，得到 $\text{[math]}$ ．
1. （1）请你直接写出点 $\text{[math]}$ ， $\text{[math]}$ 的坐标；
2. （2）平行四边形 $\text{[math]}$ 与 $\text{[math]}$ 的重叠部分的形状是，重叠部分的面积是；
3. （3）在平面内是否存在一点 $\text{[math]}$ ，使得以 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的四边形为平行四边形？若存在，请求出点 $\text{[math]}$ 的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
6. (2021八下·太原期中) 综合与探究：
问题情境：数学课上，同学们以直角三角形纸片为背景进行探究性活动．如图，在△ABC中，CD⊥AB于点D，AE平分∠BAC交CD于点F．
1. （1）初步分析：
  智慧小组的同学发现△CEF是等腰三角形，请你证明这一结论；
2. （2）博学小组的同学发现给△ABC添加一个条件，可使△CEF成为等边三角形．添加的条件可以是　　．（写出一种即可）
3. （3）操作探究：
  创新小组的同学从图形平移的角度进行了如下的探究，请从下面A，B两题中任选一题作答我选择（）题：
  A将△ADF沿射线AB的方向平移，使点F的对应点F恰好落在线段BC上，
  ①请在图中画出平移后的 $\text{[math]}$ ，
  ②猜想此时线段A′B与AC之间的数量关系，并说明理由．
  B将△CEF沿射线CB的方向平移，使点C的对应点恰好与点B重合，
  ①请在图中画出平移后的 $\text{[math]}$ ，
  ②连接EF′，交BD于点G，猜想此时线段EG与F′G之间的数量关系，并说明理由．
答案解析收藏纠错 + 选题
7. (2021·太原模拟) 综合与探究
如图1，直线 $\text{[math]}$ ： $\text{[math]}$ 与x轴，y轴分别交于A，B两点，抛物线 $\text{[math]}$ 经过A，B两点，与x轴的另一个交点为点C，连接 $\text{[math]}$ ，作 $\text{[math]}$ 关于直线l对称的 $\text{[math]}$ ．
1. （1）求抛物线的表达式，并直接写出点D的坐标；
2. （2）如图2，将 $\text{[math]}$ 沿着x轴向左平移t个单位长度得到 $\text{[math]}$ ，A，B，D三点的对应点分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点，当点A与点C重合时停止． $\text{[math]}$ 与 $\text{[math]}$ 交于点M， $\text{[math]}$ 与 $\text{[math]}$ 交于点N，连接 $\text{[math]}$ ，记 $\text{[math]}$ 与 $\text{[math]}$ 重叠部分的面积为S．请解答下列问题：
  ①求S与t的函数关系式；
  
  ②当 $\text{[math]}$ 轴时，求S的值；
3. （3）当（2）中的S取得最大值时，点 $\text{[math]}$ 沿着一定的路径运动到 $\text{[math]}$ 轴上的点P处，然后再沿着与x轴平行的直线运动到抛物线对称轴上的点Q处，最后运动到点C处．请直接写出点 $\text{[math]}$ 运动到点C处的最短路径的长．
答案解析收藏纠错 + 选题
8. (2021·深圳押题) 一次合作探究课上，同学们在探究问题：在Rt△ABC中，∠ACB=90°，AC=3 ， ∠ABC的平分线交AC于D ，一条直线l绕点D旋转，与AB交于点E．
1. （1）当直线l⊥AC时(如图1)，将BD平移到CF的位置，此时点F恰好在直线l上，四边形BCFD是平行四边形吗？请说明理由；
2. （2）当直线l⊥AB时（如图2），若AE= $\text{[math]}$ ，求CD的长；
3. （3）探究小组发现：在（2）的线段长度下，当直线l绕点D旋转时（如图3），如果与BC的延长线交于G时， $\text{[math]}$ 的值始终不变．请你帮他们证明并求出这个定值．
答案解析收藏纠错 + 选题
9. (2020九上·长兴开学考) 在一次数学研究性学习中，小兵将两个全等的直角三角形纸片ABC和DEF拼在一起，使点A与点F重合，点C与点D重合(如图1)，其中∠ACB=∠DFE=90° ，BC=EF=3cm，AC=DF=4 cm，并进行如下研究活动。

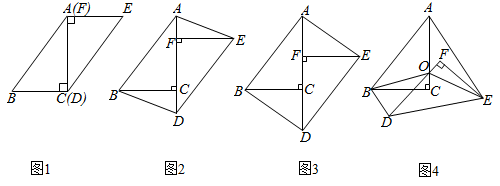
活动一：将图1中的纸片DEF沿AC方向平移，连结AE，BD(如图2)，当点F与点C重合时停止平移。

活动二：在图3中，取AD的中点O，再将纸片DEF绕点O顺时针方向旋转a度(0≤a≤90)，连结OB，OE(如图4)。
1. （1）图2中的四边形ABDE是平行四边形吗？请说明理由。
2. （2）当纸片DEF平移到某一位置时，小兵发现四边形ABDE为矩形(如图3)。求AF的长。
3. （3）当EF平分∠AEO时，探究OF与BD的数量关系，并说明理由。
答案解析收藏纠错 + 选题

二、实践探究题

10. (2023九上·西安开学考) 综合与实践
综合与实践课上，老师让同学们以“三角板的平移”为主题开展数学活动．
1. （1）操作判断
  操作一：将一副等腰直角三角板两斜边重合，按图1放置；
  操作二：将三角板 $\text{[math]}$ 沿 $\text{[math]}$ 方向平移（两三角板始终接触）至图2位置．
  根据以上操作，填空：
  ①图1中四边形 $\text{[math]}$ 的形状是；
  ②图2中 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是；四边形 $\text{[math]}$ 的形状是．
2. （2）迁移探究
  小航将一副等腰直角三角板换成一副含 $\text{[math]}$ 角的直角三角板，继续探究，已知三角板 $\text{[math]}$ 边长为 $\text{[math]}$ ，过程如下：
  将三角板 $\text{[math]}$ 按（1）中的方式操作，如图3，在平移过程中，四边形 $\text{[math]}$ 的形状能否是菱形，若不能，请说明理由，若能，请求出 $\text{[math]}$ 的长．
3. （3）拓展应用
  在（2）的探究过程中：
  
  ①当 $\text{[math]}$ 为等腰三角形时，请直接写出 $\text{[math]}$ 的长；
  
  ②直接写出 $\text{[math]}$ 的最小值．
答案解析收藏纠错 + 选题
11. (2021八下·灵石期中) 综合与实践
【问题情境】

在数学综合实践课上，老师让同学用两张全等的等腰三角形纸片进行拼摆，并探究摆放后所构成的图形之间的关系．如图1， $\text{[math]}$ ， AB＝AC，DE＝DF．

【操作发现】
1. （1）勤奋小组的同学把这两张纸片完全重合，点A与点D重合，将 $\text{[math]}$ 绕点D逆时针方向旋转到如图2的位置，连接BE和CF．他们发现BE与CF之间存在着一定的数量关系，请写出这些关系并说明理由；
2. （2）创新小组的同学在勤奋小组的启发下，把 $\text{[math]}$ 垂直翻转，再平移使得点E与点A重合，点D与点C重合，再将 $\text{[math]}$ 沿射线CA的方向向上平移到图3的位置，连接BE和CF，他们发现了BE和CF之间的数量和位置关系，请写出这些关系并说明理由；
3. （3）请你参照以上操作，将图1中的 $\text{[math]}$ 在同一平面内进行平移、旋转、翻转等图形变换，构成一种与图2和图3都不相同的图形，在图4中画出构造出的新图形，标明字母，说明构图方法，写出你发现的结论，不必证明．
答案解析收藏纠错 + 选题