吉林省长春市吉林省第二实验学校2023-2024学年九年级下...

更新时间：2024-05-07 浏览次数：10 类型：月考试卷

一、选择題（每小题3分，共24分）

1. (2024七上·柯桥月考) $\text{[math]}$ 的相反数是（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九下·长春月考) 历时七年的建设，全长407000米的济南至郑州高速铁路于2023年12月8日10时58分实现全线贯通运营，济南至郑州最快1小时43分可达，济郑高铁的开通将结束两个人口亿级的大省没有高铁直连的历史．将407000用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024七下·竞秀期中) 若 $\text{[math]}$ ，则“□”内应填的运算符号为（　　）

A . + B . ﹣ C . × D . ÷

答案解析收藏纠错 + 选题
4. (2024九下·长春月考) 如图是正方体的展开图，将它折叠成正方体后“龙”字的对面是（）

A . 学 B . 业 C . 进 D . 步

答案解析收藏纠错 + 选题
5. (2024九下·长春月考) 在下列现象中，可以用基本事实“两点之间线段最短”来解释的是（）

A . 木工弹线 B . 泥工砌墙 C . 弯路改直 D . 射击瞄准

答案解析收藏纠错 + 选题
6. (2024九下·长春月考) 如图，滑雪场有一坡角为 $\text{[math]}$ 的滑雪道，滑雪道 $\text{[math]}$ 长为150米，则滑雪道的坡顶到坡底的竖直高度 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ 米 B . $\text{[math]}$ 米 C . $\text{[math]}$ 米 D . $\text{[math]}$ 米

答案解析收藏纠错 + 选题
7. (2024九下·长春月考) 如图，在 $\text{[math]}$ 中，根据尺规作图痕迹，下列说法不一定正确的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九下·长春月考) 如图，点A在双曲线 $\text{[math]}$ 上，点B在双曲线 $\text{[math]}$ 上， $\text{[math]}$ 轴，过点A作 $\text{[math]}$ 轴于D ，连接 $\text{[math]}$ ，与 $\text{[math]}$ 相交于点C ，若 $\text{[math]}$ ，则k的值为（）

A . 8 B . 12 C . 16 D . 18

答案解析收藏纠错 + 选题

二、填空题（每小题3分，18分）

9. (2024九上·麒麟月考) 因式分解 $\text{[math]}$ .

答案解析收藏纠错 + 选题
10. (2024九下·河源月考) 若关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有两个相等的实数根，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2024九下·长春月考) 2024年元旦期间，小华和家人到公园景区游玩．公园里有大小两种游船，小华发现：1艘大船与1艘小船一次满载游客共26人，2艘大船与3艘小船一次满载游客共60人．若设一艘大船一次满载人数为x人，则根据题意x的值为．

答案解析收藏纠错 + 选题
12. (2024九下·长春月考) 如图，多边形 $\text{[math]}$ 为 $\text{[math]}$ 内接正五边形， $\text{[math]}$ 与 $\text{[math]}$ 相切于点 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2024九下·长春月考) 如图，在平行四边形 $\text{[math]}$ 中，以C为位似中心，作平行四边形 $\text{[math]}$ 的位似平行四边形 $\text{[math]}$ ，且与原图形的位似比为2∶3，连接 $\text{[math]}$ ，若平行四边形 $\text{[math]}$ 的面积为20，则 $\text{[math]}$ 与 $\text{[math]}$ 的面积之和为．

答案解析收藏纠错 + 选题
14. (2024九下·长春月考) 如图，在平面直角坐标系中，点 $\text{[math]}$ 在第二象限，以 $\text{[math]}$ 为顶点的抛物线 $\text{[math]}$ 经过原点，与 $\text{[math]}$ 轴负半轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ 在抛物线上，且位于点 $\text{[math]}$ 、 $\text{[math]}$ 之间（ $\text{[math]}$ 不与 $\text{[math]}$ 、 $\text{[math]}$ 重合）.若四边形 $\text{[math]}$ 的周长为14， $\text{[math]}$ 的周长大于8，则 $\text{[math]}$ 的取值范围为．

答案解析收藏纠错 + 选题

三、解答题（共78分）

15. (2024七下·合浦期中) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2024九下·长春月考) 2023年9月23日，第19届亚运会在杭州开幕，电子竞技首次成为亚运会正式比赛项目，小明和小张是电竞游戏的爱好者，他们相约一起去现场为中国队加油，现场的观赛区分为A、B、C、D四个区域，购票以后系统随机分配观赛区域．请用画树状图或列表等方法求出小明和小张在同一区域观看比赛的概率。

答案解析收藏纠错 + 选题
17. (2024九下·长春月考) 阅读，正如一束阳光，孩子们无论在哪儿，都可以感受到阳光的照耀，都可以通过阅读触及更广阔的世界．市教育局向中小学生推出“童心读书会”分享活动．甲、乙两同学分别从距离活动地点1200米和1800米的两地同时出发，参加分享活动．乙同学的速度是甲同学的速度的1.2倍，甲同学比乙同学提前4分钟到达活动地点．求甲、乙两同学的速度．

答案解析收藏纠错 + 选题
18. (2024九下·长春月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点D ，以点D为圆心， $\text{[math]}$ 为半径作圆交 $\text{[math]}$ 于点E ．
1. （1）求证： $\text{[math]}$ 与 $\text{[math]}$ 相切；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
19. (2024九下·长春月考) 春节是中国重要的传统节日之一，我校组织学生参加关于中国传统文化知识的线上测试活动．为了了解七、八年级学生此次线上测试活动的成绩情况，分别随机在七、八年级各抽取了10名学生的成绩（百分制，单位：分）进行整理、描述和分析（学生成绩得分用x表示，共分为三个等级：合格 $\text{[math]}$ ，良好 $\text{[math]}$ ，优秀 $\text{[math]}$ ），下面给出了部分信息：
七年级10名学生的成绩：83，84，84，88，89，89，89，95，95，98．
八年级10名学生的成绩中“良好”等级包含的所有数据为：86，86，86，90，94．
抽取的七、八年级学生测试成绩统计表
年级
平均数
中位数
众数
“优秀”等级所占百分比
七
89.4
89
a
$\text{[math]}$
八
89.4
b
86
$\text{[math]}$
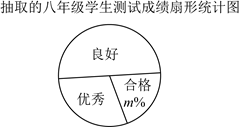
根据以上信息，解答下列问题：
1. （1）填空： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）根据以上数据，你认为该学校哪个年级的学生测试成绩更好？请说明理由（写出一条理由即可）．
3. （3）如果我校七年级有学生3500人，八年级有学生2800人，估计我校七、八年级此次线上测试成绩良好的总人数．
答案解析收藏纠错 + 选题
20. (2024九下·长春月考) 如图是由边长为1的小正方形构成的网格，每个小正方形的顶点叫做格点， $\text{[math]}$ 的顶点在格点上，请仅用无刻度的直尺在给定网格中画图，保留连线的痕迹，按步骤完成下列问题：
1. （1）如图1，已知点 $\text{[math]}$ 、A、 $\text{[math]}$ 均在格点上，求作点A关于直线 $\text{[math]}$ 的对称点 $\text{[math]}$ ，连结 $\text{[math]}$ ；
2. （2）如图2. $\text{[math]}$ 的顶点均在格点上，格点 $\text{[math]}$ 是 $\text{[math]}$ 边上一点，请在线段 $\text{[math]}$ 上找一点 $\text{[math]}$ ，连结 $\text{[math]}$ ，使 $\text{[math]}$ ；
3. （3）如图3. $\text{[math]}$ 的顶点均在格点上，求作点 $\text{[math]}$ 关于直线 $\text{[math]}$ 的对称点 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2024九下·长春月考) 图1是煤油温度计，该温度计的左侧是华氏温度（ $\text{[math]}$ ），右侧是摄氏温度（ $\text{[math]}$ ）．华氏温度与摄氏温度之间存在着某种函数关系，小明通过查阅资料和观察温度计，得到了如表所示的数据．
摄氏温度值 $\text{[math]}$
0
10
20
30
40
华氏温度值 $\text{[math]}$
32
50
68
86
104
1. （1）在如图2所示的平面直角坐标系中描出上表相应的点，并用平滑的线进行连接；
2. （2）求y与x之间的函数解析式；
3. （3）某种疫苗需低温保存，其活性只能在某温度区间（摄氏温度）内维持，在该温度区间内，任意摄氏温度与其对应的华氏温度的数值相差的最大值为16．求该温度区间的最大温差是多少摄氏度．
答案解析收藏纠错 + 选题
22. (2024九下·长春月考) 【模型建立】：如图1，在正方形中，E ， F分别是边 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，探究图中线段 $\text{[math]}$ 之间的数量关系．
1. （1）小宋的探究思路如下：延长 $\text{[math]}$ 到点G ，使 $\text{[math]}$ ，连接 $\text{[math]}$ ，先证明 $\text{[math]}$ ，再证明 $\text{[math]}$ ． $\text{[math]}$ 之间的数量关系为．若 $\text{[math]}$ ，则 $\text{[math]}$ ．
2. （2）【模型应用】：
  如图2，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ，点F为 $\text{[math]}$ 中点， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
3. （3）【拓展提升】：
  通过对图2的分析，小宋同学在深入思考后，他发现一个很有意思的结论，若 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ ．（用含a、b的代数式表示）
答案解析收藏纠错 + 选题
23. (2024九下·长春月考) 在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 上一点． $\text{[math]}$ ， $\text{[math]}$ 从点E出发，沿折线 $\text{[math]}$ 以每秒3个单位长度的速度运动，到D停止．连接 $\text{[math]}$ ，将线段 $\text{[math]}$ 绕点E顺时针旋转 $\text{[math]}$ 得到线段 $\text{[math]}$ ．连接 $\text{[math]}$ ．设点P的运动时间为t秒．
1. （1）用 $\text{[math]}$ 表示线段 $\text{[math]}$ 的长度；
2. （2）连接 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
3. （3）当点 $\text{[math]}$ 在平行四边形 $\text{[math]}$ 的对角线上时，求 $\text{[math]}$ 的值；
4. （4）连接 $\text{[math]}$ ．当 $\text{[math]}$ 分线段 $\text{[math]}$ 为 $\text{[math]}$ 的两部分时，直接写出t的值．
答案解析收藏纠错 + 选题
24. (2024九下·长春月考) 在平面直角坐标系中，抛物线 $\text{[math]}$ 的对称轴为直线 $\text{[math]}$ ，点P、Q都是该抛物线上的点，P、Q的横坐标分别为m ， $\text{[math]}$ ，当点P、Q不重合时，连结PQ ．
1. （1）求该抛物线的解析式；
2. （2）当 $\text{[math]}$ 时，求点P的坐标；
3. （3）当线段PQ与对称轴为 $\text{[math]}$ 相交时，设其交点为M ，当M不与P或Q重合时，以MQ为一边构造矩形MQGN ，其中 $\text{[math]}$ ，同时使得点Q、G、N在 $\text{[math]}$ 的同侧．
  ①当抛物线在矩形MQGN的内部任意一点的纵坐标恒为负数时，求m的取值范围；
  ②当矩形MQGN被x轴分为面积相等的两部分时，直接写出m的值．
答案解析收藏纠错 + 选题