2024年人教A版高二下学期数学期中模拟试卷二

更新时间：2024-04-23 浏览次数：28 类型：期中考试

一、选择题（每题5分，共40分）

1. (2024高一下·武鸣月考) 已知 $\text{[math]}$ 为实数，复数 $\text{[math]}$ 为纯虚数，则 $\text{[math]}$ （）

A . -1 B . 1 C . -2 D . 2

答案解析收藏纠错 + 选题
2. (2023高二上·成都月考) 已知正项等比数列 $\text{[math]}$ ，则 $\text{[math]}$ ，则公比 $\text{[math]}$ 为（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题
3. (2023高二上·成都月考) 抛掷一个质地均匀的股子的试验，事件 $\text{[math]}$ 表示“小于5的偶数点出现”，事件 $\text{[math]}$ 表示“不小于5的点数出现”，则一次试验中，事件 $\text{[math]}$ 或事件 $\text{[math]}$ 至少有一个发生的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024·横县月考) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为不同的平面，m ， n ， l为不同的直线，则下列条件中一定能得到 $\text{[math]}$ 的是（）

A . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023高二上·成都月考) 直线 $\text{[math]}$ 被圆 $\text{[math]}$ 截得的弦长为（）

A . 2 B . $\text{[math]}$ C . 4 D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. “方斗”常作为盛米的一种容器，其形状是一个上大下小的正四棱台，现有“方斗”容器如图所示，已知 $\text{[math]}$ ，现往容器里加米，当米的高度是“方斗”高度的一半时，用米 $\text{[math]}$ ，则该“方斗”可盛米的总质量为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024高二下·辉南月考) 已知函数 $\text{[math]}$ 的导函数 $\text{[math]}$ 的图象如图所示，则下列结论中正确的是（）

A . 曲线 $\text{[math]}$ 在点 $\text{[math]}$ 处的切线斜率小于零 B . 函数 $\text{[math]}$ 在区间 $\text{[math]}$ 上单调递增 C . 函数 $\text{[math]}$ 在 $\text{[math]}$ 处取得极大值 D . 函数 $\text{[math]}$ 在区间 $\text{[math]}$ 内至多有两个零点

答案解析收藏纠错 + 选题
8. (2023高二上·成都月考) 已知直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 无公共交点，则 $\text{[math]}$ 的离心率的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多项选择题（每题6分，共18分）

9. (2023高二上·成都月考) 已知一组样本数据 $\text{[math]}$ ，则这组数据的（）

A . 极差为6 B . 众数为4 C . 方差为4 D . 中位数为5

答案解析收藏纠错 + 选题
10. (2023·月考) 高二年级安排甲、乙、丙三位同学到A ， B ， C ， D ， E五个社区进行暑期社会实践活动，每位同学只能选择一个社区进行活动，且多个同学可以选择同一个社区进行活动，下列说法正确的有（）

A . 所有可能的方法有 $\text{[math]}$ 种 B . 如果社区A必须有同学选择，则不同的安排方法有61种 C . 如果同学甲必须选择社区A ，则不同的安排方法有25种 D . 如果甲、乙两名同学必须在同一个社区，则不同的安排方法共有20种

答案解析收藏纠错 + 选题
11. (2024高二下·惠州月考) 在数学中，布劳威尔不动点定理是拓扑学里的一个非常重要的不动点定理，它得名于荷兰数学家鲁伊兹*布劳威尔.简单的讲就是对于满足一定条件的连续函数 $\text{[math]}$ ，存在一个点 $\text{[math]}$ ，使得 $\text{[math]}$ ，那么我们称该函数为“不动点”函数，而称 $\text{[math]}$ 为该函数的一个不动点，依据不动点理论，下列说法正确的是（）

A . 函数 $\text{[math]}$ 只有一个不动点 B . 若定义在R上的奇函数 $\text{[math]}$ ，图象上存在有限个不动点，则不动点个数是奇数 C . 函数 $\text{[math]}$ 只有一个不动点 D . 若函数 $\text{[math]}$ 在 $\text{[math]}$ 上存在两个不动点，则实数a满足 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题（每题5分，共15分）

12. (2024·扬州模拟) 若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2024·横县月考) 设 $\text{[math]}$ ， $\text{[math]}$ 是不共线的向量，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， A ， B ， D三点共线，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
14. 若函数 $\text{[math]}$ 有两个零点，则正整数 $\text{[math]}$ 的最小值为．（其中 $\text{[math]}$ 是自然对数的底数，参考数据： $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题

四、解答题（共5题，共77分）

15. (2024高三上·潮州期末) 在 $\text{[math]}$ 中，角A，B，C的对边分别为a，b，c，已知 $\text{[math]}$ ．
1. （1）求角 $\text{[math]}$ 的大小；
2. （2）若 $\text{[math]}$ 为线段 $\text{[math]}$ 延长线上一点，且 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
16. 如图所示，在三棱锥 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证：平面 $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求直线 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角的正弦值．
答案解析收藏纠错 + 选题
17. (2024高二上·越城期末) 记 $\text{[math]}$ 为等比数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和.已知 $\text{[math]}$ .
1. （1）求数列 $\text{[math]}$ 的通项公式；
2. （2）记 $\text{[math]}$ ，求数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2024高三上·北碚月考) 动点P与定点 $\text{[math]}$ 的距离和它到直线 $\text{[math]}$ 的距离的比是常数 $\text{[math]}$ ，记点P的轨迹为E.
1. （1）求E的方程；
2. （2）已知 $\text{[math]}$ ，过点 $\text{[math]}$ 的直线与曲线E交于不同的两点A ， B ，点A在第二象限，点B在x轴的下方，直线 $\text{[math]}$ ， $\text{[math]}$ 分别与x轴交于C ， D两点，求四边形 $\text{[math]}$ 面积的最大值.
答案解析收藏纠错 + 选题
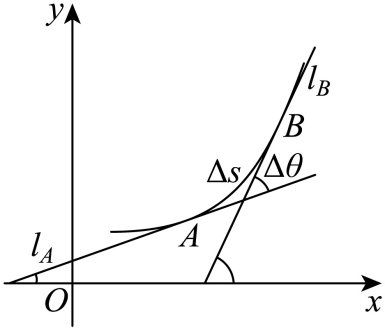
19. (2024高二下·长沙月考) 在几何学常常需要考虑曲线的弯曲程度，为此我们需要刻画曲线的弯曲程度．考察如图所示的光滑曲线C： $\text{[math]}$ 上的曲线段 $\text{[math]}$ ，其弧长为 $\text{[math]}$ ，当动点从A沿曲线段 $\text{[math]}$ 运动到B点时，A点的切线 $\text{[math]}$ 也随着转动到B点的切线 $\text{[math]}$ ，记这两条切线之间的夹角为 $\text{[math]}$ （它等于 $\text{[math]}$ 的倾斜角与 $\text{[math]}$ 的倾斜角之差）．显然，当弧长固定时，夹角越大，曲线的弯曲程度就越大；当夹角固定时，弧长越小则弯曲程度越大，因此可以定义 $\text{[math]}$ 为曲线段 $\text{[math]}$ 的平均曲率；显然当B越接近A ，即 $\text{[math]}$ 越小，K就越能精确刻画曲线C在点A处的弯曲程度，因此定义 $\text{[math]}$ （若极限存在）为曲线C在点A处的曲率．（其中y＇，y＇＇分别表示 $\text{[math]}$ 在点A处的一阶、二阶导数）
1. （1）求单位圆上圆心角为60°圆弧的平均曲率；
2. （2）求椭圆 $\text{[math]}$ 在 $\text{[math]}$ 处的曲率；
3. （3）定义 $\text{[math]}$ 为曲线 $\text{[math]}$ 的“柯西曲率”．已知在曲线 $\text{[math]}$ 上存在两点 $\text{[math]}$ 和 $\text{[math]}$ ，且P ， Q处的“柯西曲率”相同，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题