一、选择题(本大题共 10个小题,每小题3分,共30分,每小题给出的四个选项中,只有一个是符合题意的).
-
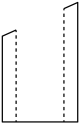
A . 9的平方根
B .  的平方根
C . 9的算术平方根
D .
的平方根
C . 9的算术平方根
D .  的算术平方根
的算术平方根
-
-
-
A . m≥-1
B . m≤1
C . m≥-1且m≠0
D . m≤1且m≠0
-
5.
(2024·剑阁模拟)
小明调查了班级里20位同学本学期购买课外书的花费情况,并将结果制成了如下统计表.在这20位同学中,本学期购买课外书的花费的众数和中位数分别是( )
捐款金额 | 100 元 | 80元 | 50元 | 30元 | 20元 |
捐款人数 | 2 | 5 | 8 | 4 | 1 |
A . 50,30
B . 50,50
C . 80,50
D . 30,50
-
6.
(2024·剑阁模拟)
如图, OA, OB 是⊙O 的半径, 连接AB, 过点O 作 OC∥AB交⊙O 于点 C, 连接AC,若∠AOB=100°,则∠BAC的度数为( )
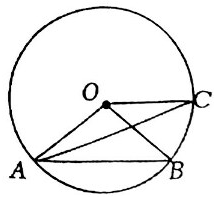
A . 15°
B . 20°
C . 25°
D . 30°
-
7.
(2024·剑阁模拟)
《姑苏繁华图》是清代苏州籍宫廷画家徐扬的作品,全长1241cm,反映的是当时苏州“商贾辐辏,百货骈阗”的市井风情.如图,已知局部临摹画面装裱前是一个长为2.6m,宽为0.6m的矩形,装裱后的长与宽的比是11:3,且四周边衬的宽度相等.设边衬的宽度为x(m),根据题意可列方程( )

-
8.
(2024·剑阁模拟)
如图,点E在正方形ABCD的对角线AC上,EF⊥AB于点 F,连接DE并延长,交边 BC于点M,交边AB的延长线于点 G.若AF=2,FB=1,则MG的长为( )
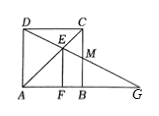
-
9.
(2024·剑阁模拟)
已知一个圆心角为

, 半径为3的扇形工件,没搬动前如图所示(A,B两点触地放置),向右滚动工件至点B再次触地时停止,则圆心O所经过的路线长是( )

-
10.
(2024·剑阁模拟)
如图,抛物线

的对称轴为x=-1,且过点(

, 有下列结论:①abc>0; ②a-2b+4c>0; ③25a-10b+4c=0; ④3b+2c>0;其中正确的结论的个数是( )

A . 1
B . 2
C . 3
D . 4
二、填空题(本大题共6个小题,每小题4分,共24分,把正确答案直接填写在答题卡对应题目的横线上).
-
-
12.
(2024·剑阁模拟)
纳米(Nanometer,符号:nm),即为毫微米,是长度单位,1纳米=10
-9米.已知一根头发的直径约为50000纳米,用科学记数法应表示为
米.
-
13.
(2024·剑阁模拟)
在一个不透明的袋子中,装有五个分别标有数字-、

,

, 0,2,π的小球, 这些小球除数字外其他完全相同.从袋子中随机摸出两个小球,两球上的数字之积恰好是有理数的概率为
.
-
14.
(2024·剑阁模拟)
如图,在数轴上,点A 表示的数是1,点B 表示的数是5,以AB为底,作腰长为6的等腰△ABC, 过点C作AB边上的高 CD,以点 D为圆心,CD 长为半径画弧交数轴于点M,则点 M 表示的数是
.

-
15.
(2024·剑阁模拟)
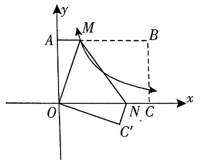
如图,在平面直角坐标系中,C,A 分别为x轴、y轴正半轴上的点,以 OA,OC为边,在第一象限内作矩形OABC,且

将矩形 OABC翻折,使点 B与原点O 重合,折痕为 MN,点C 的对应点 C'落在第四象限,过 M点的反比例函数

的图象恰好过MN的中点,则点 C
'的坐标为
.
-
16.
(2024·剑阁模拟)
如图,在△ABC中,∠ACB=90°,∠A=30°,BC=2,点D是AB上的动点,以 DC为斜边作等腰直角△DCE,点E 和点A 位于 CD的两侧,连接BE,则BE 的最小值是
.
三、解答题(本大题共 10个小题,共96分,要求写出必要的解答步骤或证明过程).
-
-
-
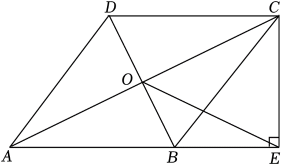
19.
(2024·剑阁模拟)
如图,在四边形
ABCD中,
AB∥
DC ,
AB=
AD , 对角线
AC ,
BD交于点
O ,
AC平分∠
BAD , 过点
C作
CE⊥
AB交
AB的延长线于点
E , 连接
OE .
-
-
-
20.
(2024·剑阁模拟)
某校化学教学组的老师们在九年级随机抽取了部分学生,就“你最擅长的化学实验是什么”进行了问卷调查,选项为常考的五个实验:A.高锰酸钾制取氧气; B.电解水;C.木炭还原氧化铜; D.一氧化碳还原氧化铜; E.铁的冶炼.要求每个学生必选且只能选择一项,并将调查结果绘制成如下不完整的条形统计图和扇形统计图:
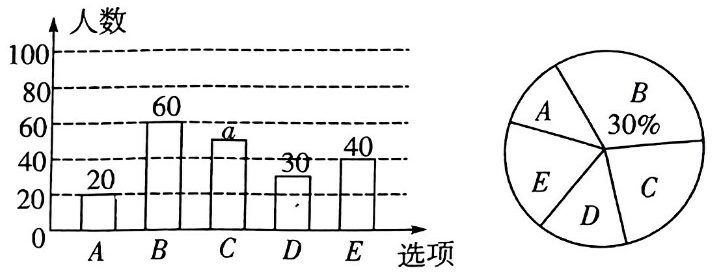
请结合统计图回答下列问题:
-
(1)
填空: a=, E所对应的扇形圆心角度数是;
-
(2)
请你根据调查结果,估计该校九年级1100名学生中有多少人最擅长的实验是“D.一氧化碳还原氧化铜”?
-
(3)
某堂化学课上,小华学到了这样一个知识:将二氧化碳通入澄清石灰水,澄清石灰水会变浑浊.已知本次调查的五个实验中,C,D,E 三个实验均能产生二氧化碳,若小华从五个实验中任意选做两个,请用列表或画树状图的方法求两个实验所产生的气体均能使澄清石灰水变浑浊的概率.
-
21.
(2024·剑阁模拟)
某“综合与实践”活动小组的同学在学习了解直角三角形的知识后,想要自主设计一道试题,他们在公园测量了如图①所示健身器材的数据,并绘制了其底座的简化示意图(如图②) ,设计题目如下:该款健身器材的座位 MN平行于地面,支架

支架AB与座位 MN的夹角∠BAN=70°, 与支架BC的夹角∠ABC为115°,求座位 MN距离地面的高度. (结果精确到0.1cm.参考数据:s

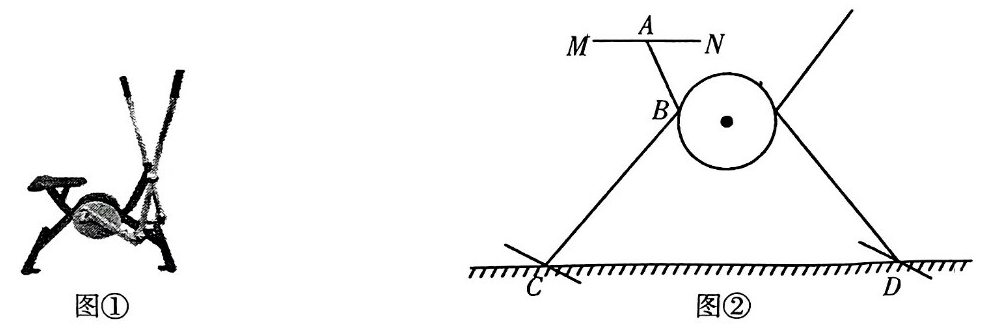
-
22.
(2024·剑阁模拟)
加强劳动教育,落实五育并举.某中学在当地政府的支持下,建成了一处劳动实践基地.2024 年计划将其中1000m
2的土地全部种植甲乙两种蔬菜.经调查发现:甲种蔬菜种植成本y(单位:元/m
2)与其种植面积x(单位:m
2)的函数关系如图所示,其中2

;乙种蔬菜的种植成本为50元/m
2.
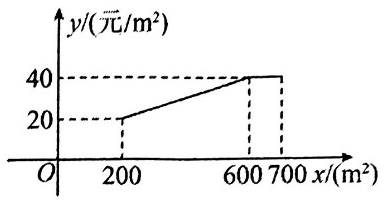
-
-
(2)
设 2024年甲乙两种蔬菜总种植成本为 W 元,如何分配两种蔬菜的种植面积,使 W 最小?
-
(3)
学校计划今后每年在这1000m2土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降,若甲种蔬菜种植成本平均每年下降10%,乙种蔬菜种植成本平均每年下降a%,当a为何值时,2026年的总种植成本为28920元?
-
23.
(2024·剑阁模拟)
如图,菱形ABCD 的边AB在x轴上, 点A 的坐标为(1,0),点D(4,4)在反比例函数

(x>0)的图象上,直线

经过点C,与y轴交于点E,连接AC,AE.
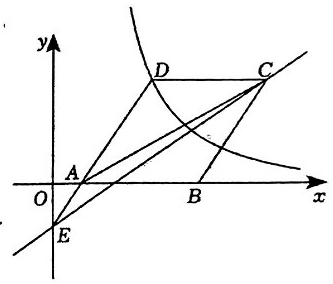
-
-
-
-
24.
(2024·剑阁模拟)
如图,⊙O是△ABC 的外接圆,AB是⊙O的直径,延长BC 至点D, 使(

连接AD交⊙O于点E,连接BE,过点 C作 CF∥BE交AD 于点 F.
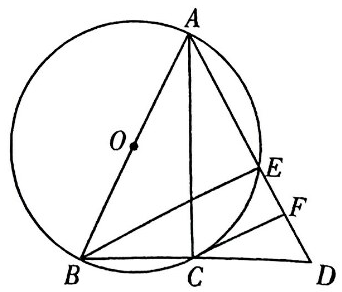
-
-
-
25.
(2024·剑阁模拟)
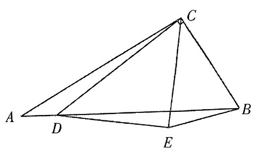
探究式学习是新课程倡导的重要学习方式,某兴趣小组拟做以下探究:
在 中,
中, 点P 是边BC上任意一点,连接AP.把边AC沿直线AP翻折得线段AE,过点B 和点 E 的直线与AP的延长线相交于点 D,连接CD.
点P 是边BC上任意一点,连接AP.把边AC沿直线AP翻折得线段AE,过点B 和点 E 的直线与AP的延长线相交于点 D,连接CD.

-
(1)
【探究一】如图1,若

则:
 的度数是 ▲ ;
的度数是 ▲ ;
②试探究线段AD,BD,DE 之间的数量关系,并说明理由;
-
(2)
【探究二】如图2,若

试探究线段AD,BD,DE之间的数量关系,并说明理由;
-
(3)
【拓展运用】在图2中,若

求

的值.
-
26.
(2024·剑阁模拟)
如图,在平面直角坐标系中,抛物线

交x轴于A(-1,0), B(3,0)两点,交y轴于点 C.
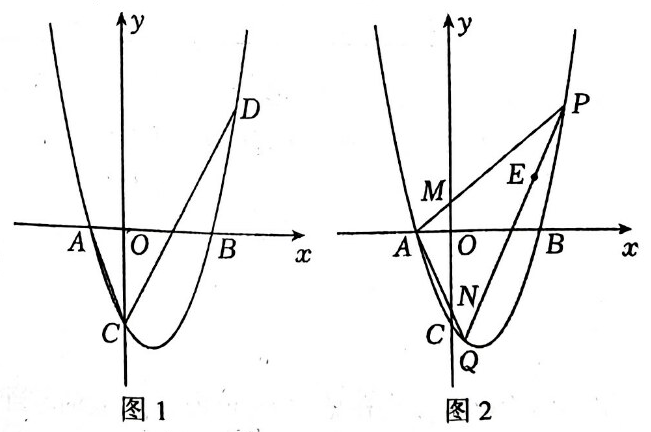
-
-
(2)
如图1,若在x轴上方的抛物线上存在一点 D,使得

, 求点 D 的坐标;
-
(3)
如图2,平面上一点 E(3,2),过点E 作任意一条直线交抛物线于 P、Q两点,连接AP、AQ,分别交y轴于M、N两点,则OM与ON的积是否为定值? 若是,求出此定值;若不是,请说明理由.
 B .
B . 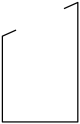 C .
C . 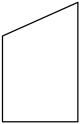 D .
D . 











中,
点P 是边BC上任意一点,连接AP.把边AC沿直线AP翻折得线段AE,过点B 和点 E 的直线与AP的延长线相交于点 D,连接CD.

的度数是 ▲ ;