命题新趋势3 真实情境（1）——2024年北师大版数学八（下...

更新时间：2024-06-02 浏览次数：27 类型：复习试卷

一、三角形的证明

1. (2024八下·深圳期末) 如图，三座商场分别坐落在A、B、C所在位置，现要规划一个地铁站，使得该地铁站到三座商场的距离相等，该地铁站应建在（）

A . 三角形三条中线的交点 B . 三角形三条高所在直线的交点 C . 三角形三个内角的角平分线的交点 D . 三角形三条边的垂直平分线的交点

答案解析收藏纠错 + 选题
2. (2024八下·襄城期末) 我国是最早了解勾股定理的国家之一．据《周髀算经》记载，勾股定理的公式与证明是在商代由商高发现的，故又称之为“商高定理”；三国时代的蒋铭祖对《蒋铭祖算经》内的勾股定理作出了详细注释，并给出了另外一个证明．下面四幅图中，不能证明勾股定理的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024八下·江门期中) 如图，在 $\text{[math]}$ 港有甲、乙两艘船，若甲船沿北偏东60°的方向以每小时8海里速度前进，乙船沿南偏东某方向以每小时15海里速度前进，2小时后甲船到 $\text{[math]}$ 岛，乙船到 $\text{[math]}$ 岛，两岛相距34海里，则乙船的航行方向是（）

A . 南偏东30° B . 南偏东40° C . 南偏东50° D . 南偏东60°

答案解析收藏纠错 + 选题
4. (2024八下·桂林期中) 小明用四根长度相同的木条制作了能够活动的菱形学具，他先活动学具成为图1所示菱形，并测得∠B＝60°，对角线AC＝20cm ，接着活动学具成为图2所示正方形，则图2中对角线AC的长为（）

A . 20cm B . 30cm C . 40cm D . 20 $\text{[math]}$ cm

答案解析收藏纠错 + 选题
5. (2024八下·潮南月考) 一块钢板的形状如图所示，已知AB＝12cm，BC＝13cm，CD＝4cm，AD＝3cm，∠ADC＝90°，则这块钢板的面积是 cm² ．

答案解析收藏纠错 + 选题
6. (2024八下·肇源开学考) 三条公路两两相交，要在该平面内修建一个加油站，使加油站到三条公路的距离都相等，则满足条件的加油站可以建处。

答案解析收藏纠错 + 选题
7. (2024八下·港北期中) 如图，学校要对一块两直角边长分别为 $\text{[math]}$ 和 $\text{[math]}$ 的直角三角形花圃进行扩建，计划将其扩建成等腰三角形，且扩建部分是以 $\text{[math]}$ 为直角边的直角三角形，则符合要求的方案共有种．

答案解析收藏纠错 + 选题
8. (2024八下·岳麓月考) 如图是一块农家菜地的平面图，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则这块菜地的面积为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
9. (2024八下·克孜勒苏柯尔克孜月考) 一艘轮船以16海里/时的速度离开港口如图，向北偏东 $\text{[math]}$ 方向航行，另一艘轮船同时以12海里/时的速度向北偏西的某个方向航行，已知它们离港口 $\text{[math]}$ 后相距30海里（即 $\text{[math]}$ 海里），问另一艘轮船航行的方向是北偏西多少度

答案解析收藏纠错 + 选题

10. (2024八下·西塘月考) 阅读与思考：下面是小宇同学的数学日记，请仔细阅读并完成相应的任务．

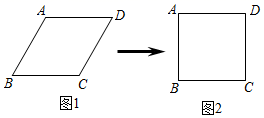
×年×月×日星期日

用等面积法解决问题

周末，我对本学期所学的内容进行了回顾与整理，发现数学中有许多方法是可以互相迁移的．

比如我们在学习整式乘法时，借助如图1所示的边长为 $\text{[math]}$ 的正方形，用两种不同的方法表示这个正方形的面积，可以得到乘法公式 ① ．

再比如学习三角形的内容时，我遇到了同样可以用等面积法解决的问题．如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求点 $\text{[math]}$ 到 $\text{[math]}$ 的距离．我们也可以利用等面积法求得点 $\text{[math]}$ 到 $\text{[math]}$ 的距离为 ② ．

总结：等面积法是一种重要的数学解题方法，在解题中，灵活运用等面积法解决相关问题，不仅可以使解题思路清晰，过程简洁，而且还能体现知识间的相互联系．

任务：

（1）请你补全小宇日记中不完整的部分：①__________，②__________．
（2）尺规作图：在图2中作 $\text{[math]}$ 的角平分线，交 $\text{[math]}$ 于点 $\text{[math]}$ （保留作图痕迹，不写作法）．
（3）在（2）的条件下，求线段 $\text{[math]}$ 的长度．

答案解析收藏纠错 + 选题

11. (2023八下·昭通期末) 为了测量一条两岸平行的河流的宽度，三个数学活动小组设计了不同的方案，他们在河南岸的点B处测得河北岸的树AB恰好在B的正北方向，测量方案如下表：

课题	测量河流宽度
工具	测量角度的仪器，标杆，皮尺等
小组	第一小组	第二小组	第三小组
测量方案	观测者从B点向东走到 $\text{[math]}$ 点，此时测得点 $\text{[math]}$ 恰好在东南方向上．	观测者从B点出发，沿着南偏西 $\text{[math]}$ 的方向走到点 $\text{[math]}$ ，此时恰好测得 $\text{[math]}$ ．	观测者从B点向东走到 $\text{[math]}$ 点，在 $\text{[math]}$ 点插上一面标杆，继续向东走相同的路程到达 $\text{[math]}$ 点后，一直向南走到点 $\text{[math]}$ ，使得树、标杆、人在同一直线上．
测量示意图

（1）第一小组认为要知道河宽 $\text{[math]}$ ，只需要知道线段的长度．
（2）第二小组测得 $\text{[math]}$ 米，则 $\text{[math]}$ ．
（3）第三小组认为只要测得 $\text{[math]}$ 就能得到河宽 $\text{[math]}$ ，你认为第三小组的方案可行吗?如果可行，请给出证明；如果不可行，请说明理由．

答案解析收藏纠错 + 选题

二、不等式

12. (2024八下·化州月考) 某种药品的说明书上，贴有如图所示的标签，一次服用这种药品的剂量范围是（　　） $\text{[math]}$ ．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
13. (2024七下·桐柏期中) 如图是某校园内对汽车的限速标志，表示该校园内汽车行驶的速度 $\text{[math]}$ （千米/小时）应满足的不等关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
14. (2024八下·花溪期中) 一次测验，有20道选择题，评分标准为：对1题给5分，错1题扣2分，不答题不给分也不扣分，小明有2道题未答，则他至少要答对几道题，总分才不会低于60分?设小明要答对 $\text{[math]}$ 道题，则根据题意可列不等式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2021八下·城阳期中) 在2021年全民读书月活动期间，小亮网购了一本《数学家的眼光》，同学们想知道书的价格，小亮让他们猜，甲说：“至多14元，”乙说：“至少15元，”丙说：“至多10元，”小亮说：“你们三个人都说错了”．则这本书的价格x（元）的范围为（　　）

A . 10＜x＜14 B . 11＜x＜14 C . 14＜x＜15 D . x＞15

答案解析收藏纠错 + 选题
16. (2024八下·龙岗期中) 如图，周日下午八年级某班小明想到A站乘公交车返校上学，发现他与公交车的距离为 $\text{[math]}$ ．假设公交车的速度是小明速度的5倍．若要保证小明不会错过这辆公交车，则小明到A站之间的距离最大为m．

答案解析收藏纠错 + 选题
17. (2024九下·振兴模拟) 为加强学生安全教育，某学校组织了“安全教育”知识竞赛，对表现优异的班级进行奖励，学校购买了若干副乒乓球拍和羽毛球拍，购买3副乒乓球拍和1副羽毛球拍共需140元；购买2副乒乓球拍和3副羽毛球拍共需210元．
1. （1）求购买1副乒乓球拍和1副羽毛球拍各需多少元；
2. （2）若学校购买乒乓球拍和羽毛球拍共30副，且总费用不超过1100元，求至少购买多少副乒乓球拍．
答案解析收藏纠错 + 选题
18. (2024八下·长安期中) 某校初二年级70名师生参加“研学旅行”活动，计划租车前往，租车收费标准如下：
车型
大巴车
（最多可坐56人）
中巴车
（最多可坐40人）
小巴车
（最多可坐28人）
每车租金（元/天）
1800
1600
1100
要完成这次“研学旅行”活动，一天租车的最低费用为元．

答案解析收藏纠错 + 选题
19. (2021八下·杏花岭月考) 如图，用长为40米的铁丝一边靠墙围成两个长方形（靠墙部分不使用铁丝），墙的长度MN＝30米，要使靠墙的AC边不小于25米，那么与墙垂直的一边AB的长度范围为．

答案解析收藏纠错 + 选题
20. (2024八下·南海期中) 某学校拟向公交公司租借 $\text{[math]}$ 两种车共8辆，用于接送八年级师生去社会实践基地参加活动．两种型号的车的载客能力和租金如下表所示：
$\text{[math]}$
$\text{[math]}$
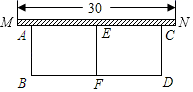
载客量（人/辆）
50
35
租金（元/辆）
450
300
设租用 $\text{[math]}$ 型车 $\text{[math]}$ 辆，
1. （1）请用代数式表示出总租金是多少
2. （2）保证租车费用不超过2900元，且八年级师生共305人，请在所有满足的租车方案中，指出花费最少的方案租用了几辆 $\text{[math]}$ 型车？
答案解析收藏纠错 + 选题
21. (2022八下·仓山期末) 公园计划购进A，B两种花卉500株，其中A花卉每株单价为6元，购买B种花卉所需费用y（单位：元）与购买数量x（单位：株）之间函数关系如图：
1. （1）求y与x的函数关系式；
2. （2）若B种花卉不超过300株，但不少于A种花卉的数量的四分之一，请你设计购买方案，使总费用最低，并求出最低费用.
答案解析收藏纠错 + 选题

三、平移与旋转

22. (2024八下·印江期中) 教育部门高度重视校园安全教育，要求各级各类学校从认识安全警告标志入手开展安全教育．下列安全图标是中心对称图形的是（）

A . 注意安全 B . 急救中心 C . 水深危险 D . 禁止攀爬

答案解析收藏纠错 + 选题
23. (2024八下·灯塔期末) 下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（　　）

A . 赵爽弦图 B . 笛卡尔心形线 C . 科克曲线 D . 斐波那契螺旋线

答案解析收藏纠错 + 选题
24. (2023八下·李沧期末) 2023年5月30日，神舟十六号载人飞船发射取得圆满成功，此次任务是我国载人航天工程进入空间站应用与发展阶段的首次载人飞行任务．下列航天图标，其文字上方的图案是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
25. (2023八下·市南区期末) 我国将在2060年实现碳中和，新能源、绿色能源将成为产业发展的新趋势，下列新能源环保图标中是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
26. (2024七下·宜春期中) 如图，把三角板的斜边紧靠直尺平移，一个顶点从刻度“5”平移到刻度“10”，则顶点C平移的距离CC＇＝.

答案解析收藏纠错 + 选题
27. (2023八下·江油月考) 某会展中心在会展期间准备将高5m、长13m、宽2m的楼道铺上地毯，已知地毯每平方米20元，请你帮助计算一下，铺完这个楼道至少需要元．

答案解析收藏纠错 + 选题
28. (2023八下·罗湖期末) 如图，在一块长方形草坪中间，有一条处处 $\text{[math]}$ 宽的“曲径”，则“曲径”的面积为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
29. (2023八下·莲湖期中) 某宾馆重新装修后，准备在大厅的楼梯上铺设一种红地毯，已知这种地毯每平方米售价70元，楼梯宽2米，楼梯侧面及相关数据如图所示，求买地毯至少需要多少元？

答案解析收藏纠错 + 选题
30. (2024八下·南海月考) 综合与实践，问题情境：活动课上，同学们以等腰三角形为背景展开有关图形旋转的探究活动，如图1，已知 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．将 $\text{[math]}$ 从图1的位置开始绕点A逆时针旋转，得到 $\text{[math]}$ （点D ， E分别是点B ， C的对应点），旋转角为 $\text{[math]}$ ，设线段AD与BC相交于点M ，线段DE分别交BC ， AC于点O ， N ．
1. （1）特例分析：如图2，当旋转到 $\text{[math]}$ 时，判断 $\text{[math]}$ 的形状并说明理由；
2. （2）探究规律：如图3，在 $\text{[math]}$ 绕点A逆时针旋转过程中，“求真”小组的同学发现线段DM始终等于线段CN ，请你证明这一结论；
3. （3）拓展延伸：①请求出当 $\text{[math]}$ 是等腰三角形时旋转角 $\text{[math]}$ 的度数；
  ②在图3中，作直线BD ， CE交于点P ，直接写出当 $\text{[math]}$ 时旋转角 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题