题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /中考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

山东省滨州市2024年中考数学试卷

更新时间：2024-07-03 浏览次数：59 类型：中考真卷

一、选择题：本大题共8个小题，每小题3分，满分24分．每小题只有一个选项符合题目要求．

1. (2024七上·东城期中) $\text{[math]}$ 的绝对值是（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024·滨州) 如图，一个三棱柱无论怎么摆放，其主视图不可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024八上·南宁开学考) 数学中有许多精美的曲线，以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡尔心形线”．其中不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2024·滨州) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024·滨州) 若点 $\text{[math]}$ 在第二象限，那么a的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024·滨州) 在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示：
成绩/m
1.50
1.60
1.65
1.70
1.75
1.80
人数
2
3
2
3
4
1
某同学分析上表后得出如下结论：
①这些运动员成绩的平均数是1.65；
②这些运动员成绩的中位数是1.70；
③这些运动员成绩的众数是1.75．
上述结论中正确的是（）

A . ②③ B . ①③ C . ①② D . ①②③

答案解析收藏纠错 + 选题
7. (2024·滨州) 点 $\text{[math]}$ 和点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ （ $\text{[math]}$ 为常数）的图象上，若 $\text{[math]}$ ，则 $\text{[math]}$ 的大小关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024·滨州) 刘徽（今山东滨州人）是魏晋时期我国伟大的数学家，中国古典数学理论的奠基者之一，被誉为“世界古代数学泰斗”．刘徽在注释《九章算术》时十分重视一题多解，其中最典型的是勾股容方和勾股容圆公式的推导，他给出了内切圆直径的多种表达形式．如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 的长分别为 $\text{[math]}$ ．则可以用含 $\text{[math]}$ 的式子表示出 $\text{[math]}$ 的内切圆直径 $\text{[math]}$ ，下列表达式错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题：本大题共8个小题，每小题3分，满分24分．

9. (2024九上·哈尔滨开学考) 若分式 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是.

答案解析收藏纠错 + 选题
10. (2024七下·南昌期中) 写出一个比 $\text{[math]}$ 大且比 $\text{[math]}$ 小的整数是.

答案解析收藏纠错 + 选题
11. (2024九上·南昌月考) 将抛物线 $\text{[math]}$ 先向右平移1个单位长度，再向上平移2个单位长度，则平移后抛物线的顶点坐标为．

答案解析收藏纠错 + 选题
12. (2024·滨州) 一副三角板如图1摆放，把三角板 $\text{[math]}$ 绕公共顶点O顺时针旋转至图2，即 $\text{[math]}$ 时， $\text{[math]}$ 的大小为．

答案解析收藏纠错 + 选题
13. (2024·滨州) 如图，在 $\text{[math]}$ 中，点D ， E分别在边 $\text{[math]}$ 上．添加一个条件使 $\text{[math]}$ ，则这个条件可以是．（写出一种情况即可）

答案解析收藏纠错 + 选题
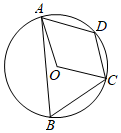
14. (2024·滨州) 如图，四边形ABCD内接于⊙O，若四边形AOCD是菱形，∠B的度数是．

答案解析收藏纠错 + 选题
15. (2024·滨州) 如图，四边形AOBC四个顶点的坐标分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，在该平面内找一点P ，使它到四个顶点的距离之和 $\text{[math]}$ 最小，则P点坐标为．

答案解析收藏纠错 + 选题
16. (2024·滨州) 如图，在边长为1的正方形网格中，点A ， B均在格点上．
⑴ $\text{[math]}$ 的长为；
⑵请只用无刻度的直尺，在如图所示的网格中，画出以 $\text{[math]}$ 为边的矩形 $\text{[math]}$ ，使其面积为 $\text{[math]}$ ，并简要说明点C ， D的位置是如何找到的（不用证明）：．

答案解析收藏纠错 + 选题

三、解答题：本大题共8个小题，满分72分．解答时请写出必要的演推过程．

17. (2024·滨州) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2024·滨州) 解方程：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
19. (2024·滨州) 欧拉是历史上享誉全球的最伟大的数学家之一，他不仅在高等数学各个领域作出杰出贡献，也在初等数学中留下了不凡的足迹．设a ， b ， c为两两不同的数，称 $\text{[math]}$ 为欧拉分式．
1. （1）写出 $\text{[math]}$ 对应的表达式；
2. （2）化简 $\text{[math]}$ 对应的表达式．
答案解析收藏纠错 + 选题
20. (2024·滨州) 某校劳动实践基地共开设五门劳动实践课程，分别是A：床铺整理，B：衣物清洗，C：手工制作、D：简单烹饪、E：绿植栽培；课程开设一段时间后，季老师采用抽样调查的方式在全校学生中开展了“我最喜欢的劳动实践课程”为主题的问卷调查．根据调查所收集的数我进行整理、绘制了如下两幅不完整的统计图．
根据图中信息，请回答下列问题：
1. （1）请将条形统计图补充完整，并直接写出“手工制作”对应的扇形圆心角度数；
2. （2）若该校共有1800名学生，请你估计全校最喜欢“绿植栽培”的学生人数；
3. （3）小兰同学从B，C，D三门课程中随机选择一门参加劳动实践，小亮同学从C，D，E三门课程中随机选择一门参加劳动实践，求两位同学选择相同课程的概率．
答案解析收藏纠错 + 选题
21. (2024·滨州) 【问题背景】
某校八年级数学社团在研究等腰三角形“三线合一”性质时发现：
①如图，在 $\text{[math]}$ 中，若 $\text{[math]}$ ， $\text{[math]}$ ，则有 $\text{[math]}$ ；
②某同学顺势提出一个问题：既然①正确，那么进一步推得 $\text{[math]}$ ，即知 $\text{[math]}$ ，若把①中的 $\text{[math]}$ 替换为 $\text{[math]}$ ，还能推出 $\text{[math]}$ 吗？基于此，社团成员小军、小民进行了探索研究，发现确实能推出 $\text{[math]}$ ，并分别提供了不同的证明方法．
小军小民
证明：分别延长DB，DC至E，F两点，使得…… 证明：∵AD⊥BC，
∴△ADB 与△ADC均为直角三角形
根据勾股定理，得……

【问题解决】
1. （1）完成①的证明；
2. （2）把②中小军、小民的证明过程补充完整．
答案解析收藏纠错 + 选题
22. (2024·滨州) 春节期间，全国各影院上映多部影片，某影院每天运营成本为2000元，该影院每天售出的电影票数量y（单位：张）与售价x（单位：元/张）之间满足一次函数关系（ $\text{[math]}$ ，且x是整数），部分数据如下表所示：
电影票售价x（元/张）
40
50
售出电影票数量y（张）
164
124
1. （1）请求出y与x之间的函数关系式；
2. （2）设该影院每天的利润（利润 $\text{[math]}$ 票房收入 $\text{[math]}$ 运营成本）为w（单位：元），求w与x之间的函数关系式；
3. （3）该影院将电影票售价x定为多少时，每天获利最大？最大利润是多少？
答案解析收藏纠错 + 选题
23. (2024·滨州) 如图， $\text{[math]}$ 中，点D ， E ， F分别在三边 $\text{[math]}$ 上，且满足 $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 为平行四边形；
2. （2）若 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 为菱形；
答案解析收藏纠错 + 选题
24. (2024·滨州) 把一块三角形余料 $\text{[math]}$ （如图所示）加工成菱形零件，使它的一个顶点与 $\text{[math]}$ 的顶点M重合，另外三个顶点分别在三边 $\text{[math]}$ 上，请在图上作出这个菱形．（用尺规作图，保留作图痕迹，不写作法．）

答案解析收藏纠错 + 选题
25. (2024·滨州) 【教材呈现】
现行人教版九年级下册数学教材85页“拓广探索”第14题：
14．如图，在锐角 $\text{[math]}$ 中，探究 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的关系．（提示：分别作 $\text{[math]}$ 和 $\text{[math]}$ 边上的高．）

【得出结论】
$\text{[math]}$ ．
1. （1）【基础应用】
  在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，利用以上结论求 $\text{[math]}$ 的长；
2. （2）【推广证明】
  进一步研究发现， $\text{[math]}$ 不仅在锐角三角形中成立，在任意三角形中均成立，并且还满足 $\text{[math]}$ （R为 $\text{[math]}$ 外接圆的半径）．请利用图1证明： $\text{[math]}$ ．
3. （3）【拓展应用】
  如图2，四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．求过A ， B ， D三点的圆的半径．
答案解析收藏纠错 + 选题

试卷信息