【提升版】北师大版数学八上第三章位置与坐标单元测试卷

更新时间：2024-07-19 浏览次数：37 类型：单元试卷

一、选择题 (本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的）

1. (2024七下·京山期中) 如图是小刚画的一张脸，若用点A(1，1)表示左眼的位置，点B(3，1)表示右眼的位置，则嘴巴点C的位置可表示为（）

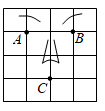
A . (2，﹣1) B . (2，1) C . (3，﹣1) D . (2，0)

答案解析收藏纠错 + 选题
2. (2023八下·卢龙期中) 下列关于有序数对的说法正确的是（）

A . （3，4）与（4，3）表示的位置相同 B . （a，b）与（b，a）表示的位置肯定不同 C . （3，5）与（5，3）是表示不同位置的两个有序数对 D . 有序数对（4，4）与（4，4）表示两个不同的位置

答案解析收藏纠错 + 选题
3. (2024八上·滨江期末) 在平面直角坐标系中，若点 $\text{[math]}$ 在第二象限，则 $\text{[math]}$ 的取值范围为 $\text{[math]}$ 　　 $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023八上·长清期中) 如图所示，A（2 $\text{[math]}$ ， 0），AB＝3 $\text{[math]}$ ，以点A为圆心，AB长为半径画弧交x轴负半轴于点C ，则点C的坐标为（　　）

A . （3 $\text{[math]}$ ， 0） B . （ $\text{[math]}$ ， 0） C . （- $\text{[math]}$ ， 0） D . （-3 $\text{[math]}$ ， 0）

答案解析收藏纠错 + 选题
5. (2023八上·包河期中) 在平面直角坐标系中，对于平面内任意一点 $\text{[math]}$ ，规定以下两种变化： $\text{[math]}$ ， $\text{[math]}$ 按照该规定： $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024八上·万源期末) 已知点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ， $\text{[math]}$ 平行于 $\text{[math]}$ 轴，则 $\text{[math]}$ 点的坐标（）

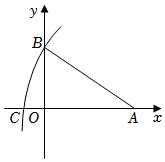
A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024八上·汉阳期末) 如图，这是平面镜成像的示意图，若以蜡烛的底部和平面镜中像的底部连线为 $\text{[math]}$ 轴，平面镜所在点的竖线为 $\text{[math]}$ 轴（镜面厚度忽略不计）建立平面直角坐标系，某时刻火焰顶部 $\text{[math]}$ 的坐标是 $\text{[math]}$ ，则此时对应的虚像 $\text{[math]}$ 的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023八上·济阳期中) 在平面直角坐标系中，对于点P（x，y），我们把点P′（﹣y+1，x+1）叫做点P伴随点，已知点A₁的伴随点为A₂ ，点A₂的伴随点为A₃ ，点A₃的伴随点为A₄ ， …，这样依次得到点A₁ ， A₂ ， A₃ ， …，A_n ， …若点A₁的坐标为（2，4），则点A₂₀₂₃的坐标为（）

A . （3，﹣1） B . （﹣2，﹣2） C . （﹣3，3） D . （2，4）

答案解析收藏纠错 + 选题

二、填空题（本大题共5小题, 每小题3分, 共15分)

9. (2024八上·南海期末) 平面直角坐标系中，点 $\text{[math]}$ 与点关于y轴对称。

答案解析收藏纠错 + 选题
10. (2024八上·新昌期末) 若点 $\text{[math]}$ 关于y轴的对称点是点 $\text{[math]}$ ，则a=．

答案解析收藏纠错 + 选题
11. (2024八上·拱墅期末) 在平面直角坐标系中，点 $\text{[math]}$ 在y轴上，则m的值为

答案解析收藏纠错 + 选题
12. (2024七下·恩施期中) 在平面直角坐标系中，点 $\text{[math]}$ 在第二象限，且该点到 $\text{[math]}$ 轴与到 $\text{[math]}$ 轴的距离相等，则 $\text{[math]}$ 点坐标为．

答案解析收藏纠错 + 选题
13. (2024七下·惠城期中) 若点B的坐标为(2，1)，AB∥y轴，且AB＝4，则点A的坐标为．

答案解析收藏纠错 + 选题

三、解答题（共7题；共61分）

14. (2024八上·滨江期末) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）若点 $\text{[math]}$ 在第二象限内，且 $\text{[math]}$ ， $\text{[math]}$ ，求点 $\text{[math]}$ 的坐标，并求 $\text{[math]}$ 的面积；
2. （2）若点 $\text{[math]}$ 在第四象限内，且 $\text{[math]}$ 的面积为8， $\text{[math]}$ ，求点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
15. (2023八上·乐平期中) 已知点P（2a-3，a+6），解答下列各题.
1. （1）点P在 $\text{[math]}$ 轴上，求出点P的坐标；
2. （2）若点P在第二象限，且它到 $\text{[math]}$ 轴、 $\text{[math]}$ 轴的距离相等，求a²⁰⁰³+2024的值.
答案解析收藏纠错 + 选题
16. (2023八上·石首期中) 如图，平面直角坐标系中有点A（﹣1，0）和y轴上一动点B（0，a），其中a＞0，以B点为直角顶点在第二象限内作等腰直角△ABC，设点C的坐标为（c，d）．
1. （1）当a＝2时，则C点的坐标为；
2. （2）动点B在运动的过程中，试判断c+d的值是否发生变化？若不变，请求出其值；若发生变化，请说明理由．
答案解析收藏纠错 + 选题
17. (2023八上·青田期末) 在直角坐标系中，长方形的边AB可表示为 $\text{[math]}$ ，边BC可表示为 $\text{[math]}$ .
1. （1）在直角坐标系中画出长方形 $\text{[math]}$ .
2. （2）边 $\text{[math]}$ 上任意一点的坐标怎样表示.
3. （3）求线段 $\text{[math]}$ 的长度.
答案解析收藏纠错 + 选题
18. (2023八上·新城期末) 已知a，b都是实数，设点P（a，b），若满足3a＝2b+5，则称点P为“新奇点”.
1. （1）判断点A（3，2）是否为“新奇点”，并说明理由；
2. （2）若点M（m-1，3m+2）是“新奇点”，请判断点M在第几象限，并说明理由.
答案解析收藏纠错 + 选题
19. (2021八上·潍坊期中) 如图，在平面直角坐标系中， $\text{[math]}$ 各顶点的坐标分别为： $\text{[math]}$
1. （1）在图中作△A′B′C′，使△A′B′C′和△ABC关于y轴对称；
2. （2）写出点A′，B′，C′的坐标；
3. （3）若△ABC内部一点M(-2，1)关于某条直线的对称点是点M(-2，-5)，写出点E(1，2)关于该条直线的对称点F的坐标．
答案解析收藏纠错 + 选题
20. (2024八上·罗湖期末) 我们学习了平移、旋转、轴对称等图形变换，这些图形变换不仅可以应用到精美的图案设计上，还可以解决生活实际问题.
1. （1）【图案设计】
  如图1，在平面直角坐标系中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
  作出 $\text{[math]}$ 关于 $\text{[math]}$ 轴的对称图形 $\text{[math]}$ ，并标注出点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）【拓展应用】
  如图1，点 $\text{[math]}$ 是 $\text{[math]}$ 轴上一动点，并且满足 $\text{[math]}$ 的值最小，请在图中找出点 $\text{[math]}$ 的位置（保留作图痕迹），并直接写出 $\text{[math]}$ 的最小值为.
3. （3）【实际应用】
  如图2，某地有一块三角形空地 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 内一点，连接 $\text{[math]}$ 后测得 $\text{[math]}$ 米，现当地政府欲在三角形空地 $\text{[math]}$ 中修一个三角形花坛 $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 边上的任意一点（不与各边顶点重合），请问 $\text{[math]}$ 的周长最少约多少米?（保留整数）（ $\text{[math]}$ ， $\text{[math]}$ ）
答案解析收藏纠错 + 选题