北师大版数学八年级上册《第六章数据的分析》单元提升测试卷

更新时间：2024-08-16 浏览次数：7 类型：单元试卷

一、选择题（每题3分，共30分）

1. (2024八上·瑞安期末) 某文具超市有 $\text{[math]}$ 四种水笔销售，它们的单价分别是5元，4元，3元，1.2元．某天的水笔销售情况如图所示，那么这天该文具超市销售的水笔的单价的平均值是（）

A . 4元 B . 4.5元 C . 3.2元 D . 3元

答案解析收藏纠错 + 选题
2. (2024八上·南明期末) 在 $\text{[math]}$ 年贵州某大学数学与统计学院的研究生入学考试中，三名考生甲、乙、丙在笔试、面试中的成绩 $\text{[math]}$ 百分制 $\text{[math]}$ 如下表所示，你觉得被录取的考生是（）
考生
笔试 $\text{[math]}$
面试 $\text{[math]}$
甲
$\text{[math]}$
$\text{[math]}$
乙
$\text{[math]}$
$\text{[math]}$
丙
$\text{[math]}$
$\text{[math]}$

A . 甲 B . 乙 C . 丙 D . 无法判断

答案解析收藏纠错 + 选题
3. (2024八上·信宜期末) 某商店销售 $\text{[math]}$ 种领口大小分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 单位： $\text{[math]}$ 的衬衫，一个月内的销量如下表：
领口大小 $\text{[math]}$
     $\text{[math]}$
     $\text{[math]}$
     $\text{[math]}$
     $\text{[math]}$
     $\text{[math]}$
销量 $\text{[math]}$ 件
     $\text{[math]}$
     $\text{[math]}$
     $\text{[math]}$
     $\text{[math]}$
     $\text{[math]}$
你认为商店最感兴趣的是这里数据的（）

A . 平均数 B . 中位数 C . 众数 D . 加权平均数

答案解析收藏纠错 + 选题
4. (2024九下·石家庄模拟) 小红同学对数据32，41，37，37，4■进行统计分析，发现“4■”的个位数字被墨水涂污看不到了，则下列统计量与被涂污数字无关的是（）

A . 方差 B . 平均数 C . 众数 D . 中位数

答案解析收藏纠错 + 选题
5. (2022八上·龙口期末) 为了落实“作业、睡眠、手机、读物、体质”等五项管理要求，了解学生的睡眠状况，某校调查了一个班50名学生每天的睡眠时间，绘成睡眠时间条形统计图如图所示，则所调查学生睡眠时间的中位数为（）

A . 6h B . 7h C . 7.5h D . 8h

答案解析收藏纠错 + 选题
6. (2023八上·莱芜期中) 一组数据 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的平均数是 $\text{[math]}$ ，方差是 $\text{[math]}$ ，则另一组数据 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的平均数和方差分别是（）

A . 3， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
7. 甲、乙两人在相同的条件下各射击10次，将每次命中的环数绘制成如图所示统计图．根据统计图得出的结论正确的是（）

A . 甲的射击成绩比乙的射击成绩更稳定 B . 甲射击成绩的众数大于乙射击成绩的众数 C . 甲射击成绩的平均数大于乙射击成绩的平均数 D . 甲射击成绩的中位数大于乙射击成绩的中位数

答案解析收藏纠错 + 选题
8. (2021八上·泰安期中) 如果样本方差S²= $\text{[math]}$ [(x₁-2)²+(x₂-2)²+(x₃-2)²+(x₄-2)²+(x₅-2)²]，则样本和x₁+x₂+x₃+x₄+x₅= （）

A . 10 B . 4 C . 5 D . 2

答案解析收藏纠错 + 选题
9. (2024九下·东海期中) 某篮球队5名场上队员的身高（单位： $\text{[math]}$ ）分别是183、187、190、200、195，现用一名身高为 $\text{[math]}$ 的队员换下场上身高为 $\text{[math]}$ 的队员，与换人前相比，场上队员身高的（）

A . 平均数变大，方差变小 B . 平均数变小，方差变大 C . 平均数变大，方差变大 D . 平均数变小，方差变小

答案解析收藏纠错 + 选题
10. (2022八上·丰顺月考) 某校共有200名学生．为了解本学期学生参加公益劳动的情况，收集了他们参加公益劳动时间（单位：小时）等数据．下图是根据数据绘制的统计图表的一部分．下面有四个推断：
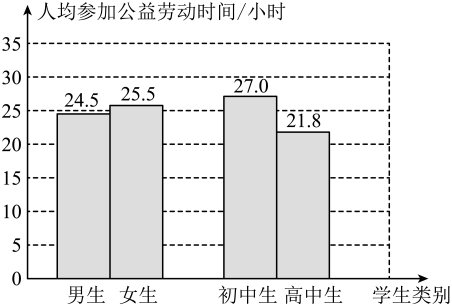
①这200名学生参加公益劳动时间的平均数一定在 $\text{[math]}$ 之间；②这200名学生参加公益劳动时间的中位数在 $\text{[math]}$ 之间；③这200名学生中的初中生参加公益劳动时间的中位数一定在 $\text{[math]}$ 之间；④这200名学生中的高中生参加公益劳动时间的中位数可能在 $\text{[math]}$ 之间．
所有合理推断的序号是（）
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
性别
男
7
31
25
30
4
女
8
29
26
32
8
学段
初中
25
36
44
11
高中

A . ①③ B . ②④ C . ①②③ D . ①②③④

答案解析收藏纠错 + 选题

二、填空题（每题3分，共18分）

11. (2023八上·芝罘期中) 某校八年级学生某科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的，评价成绩80分以上（含80分）为“优秀”.下面表中是小王同学的成绩记录：
项目
完成作业
单元测试
期末考试
成绩
65
75

若完成作业、单元检测、期末考试三项成绩按1：3：6的权重来确定期末评价成绩，小王的期末评价为优秀，那么他的期末考试最低成绩是.

答案解析收藏纠错 + 选题
12. (2023八上·达州期末) 在2015年的体育考试中某校6名学生的体育成绩统计如图所示，这组数据的中位数是．

答案解析收藏纠错 + 选题

13. (2020八上·安丘期末) 下表中记录了甲、乙、丙、丁四名运动员跳远选拔赛成绩（单位：cm）的平均数和方差．要从中选择一名成绩较高且发挥稳定的运动员参加决赛，最合适的运动员是．

	甲	乙	丙	丁
平均数 $\text{[math]}$	376	350	376	350
方差 $\text{[math]}$	12.5	13.5	2.4	5.4

答案解析收藏纠错 + 选题

14. (2020八上·银川期末) 若一组数据6，9，11，13，11，7，10，8，12的中位数是m，众数是n，则关于x，y的方程组 $\text{[math]}$ 的解是.

答案解析收藏纠错 + 选题
15. (2023八上·江北期末) 现有两组数据：甲：12，14，16，18；乙：2023，2022，2020，2019，它们的方差分别记作 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ （用“>”“=”“<”）.

答案解析收藏纠错 + 选题
16. (2023八上·莱西期中) 某班四个学习兴趣小组的学生分布如图①②，现通过对四个小组学生寒假期间所读课外书情况进行调查，并制成各小组读书情况的条形统计图③，根据统计图中的信息：这四个小组平均每人读书的本数是本．

答案解析收藏纠错 + 选题

三、解答题（共8题，共72分）

17. (2024八上·深圳期末) 某校拟派一名跳高运动员参加一项校际比赛，对甲、乙两名跳高运动员进行了8次选拔比赛，他们的成绩（单位： $\text{[math]}$ ）如下：
甲： 1. 71，1. 65，1. 68，1. 68，1. 72，1. 73，1. 68，1. 67；
乙： 1. 60，1. 74，1. 72，1. 69，1. 62，1. 71，1. 69，1. 75；
1. （1）【整理与分析】
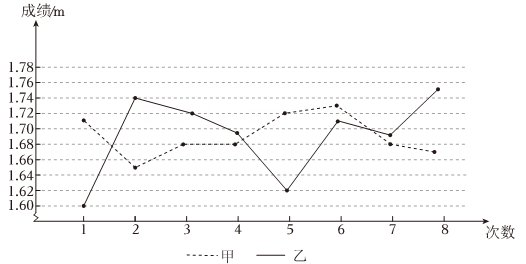
  平均数众数中位数
  甲 1.69 a 1.68
  乙 1.69 1.69 b
  
  ①由上表填空： $\text{[math]}$ ， $\text{[math]}$ ；
  ②这两人中，的成绩更为稳定。
2. （2）【判断与决案】
  经预测，跳高 $\text{[math]}$ 就很可能获得冠军，该校为了获取跳高比赛冠军，可能选哪位运动员参赛？请说明理由。
答案解析收藏纠错 + 选题
18. (2024八上·峡江期末) 某公司要在甲、乙两人中招聘一名职员，对两人的学历、能力、经验这三项进行了测试．各项满分均为10分，平均成绩高者被录用．图1是甲、乙测试成绩的条形统计图，
1. （1）分别求出甲、乙三项平均成绩，并指出会录用谁；
2. （2）若将甲、乙的三项测试成绩，按照扇形统计图（图2）各项所占之比，分别计算两人各自的综合成绩，并判断是否会改变（1）的录用结果．
答案解析收藏纠错 + 选题
19. (2024八上·罗湖期末) 杭州亚运会开幕式惊艳了世界，这背后离不开志愿者们的默默奉献，这些志愿者很多都来自高校.在志愿者招募之时， $\text{[math]}$ ， $\text{[math]}$ 两所大学就积极组织了志愿者选拔活动，对报名的志愿者进行现场测试，现从这两所大学参加测试的志愿者中分别随机抽取了20名志愿者的综合测试成绩进行整理和分析，下面给出部分信息.综合以上信息，解答下列问题：
$\text{[math]}$ ， $\text{[math]}$ 两所大学被抽取的志愿者测试成绩的平均分、中位数、众数如下表：
学校
平均分
中位数
众数
$\text{[math]}$ 校
$\text{[math]}$
$\text{[math]}$
95
$\text{[math]}$ 校
93.5
95
$\text{[math]}$
1. （1）填空： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2） $\text{[math]}$ 校志愿者的成绩的扇形统计图中的圆心角 $\text{[math]}$ ▲ °，请补全 $\text{[math]}$ 校志愿者的成绩的条形统计图；
3. （3）如果你是组委会成员，你倾向招哪所大学的志愿者?请说明理由.
答案解析收藏纠错 + 选题
20. (2024八上·福田期末) 某校开展了以“追梦新时代”为主题的读书活动，并对本校八年级学生12月份“阅读该主题相关书籍的读书量”（下面简称：“读书量”）进行了随机抽样调查，并对所有随机抽取学生的“读书量”（单位：本）进行了统计，
如图所示．

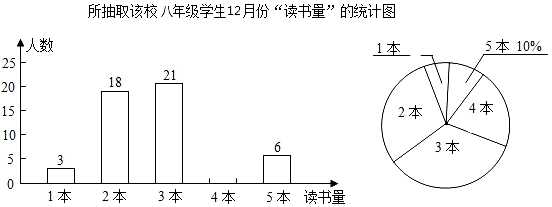
根据以上信息，解答下列问题；
1. （1）求出随机被抽查的学生总数，并补全不完整的条形统计图；
2. （2）填写本次所抽取学生12月份“读书量”的中位数为本，众数为本；
3. （3）求本次所抽取学生12月份“读书量”的平均数．
答案解析收藏纠错 + 选题
21. (2024八上·郫都期末) 某校组织了一次“校徽设计“竞赛活动，邀请 $\text{[math]}$ 名老师作为专业评委， $\text{[math]}$ 名学生代表参与民主测评，且民主测评的结果无弃权票．某作品的评比数据统计如下：
专业评委
给分 $\text{[math]}$ 单位：分 $\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$
$\text{[math]}$ 专业评委给分统计表 $\text{[math]}$
记“专业评委给分”的平均数为 $\text{[math]}$ ．
1. （1）求该作品在民主测评中得到“不赞成”的票数；
2. （2）对于该作品，问 $\text{[math]}$ 的值是多少？
3. （3）记“民主测评得分”为 $\text{[math]}$ ， “综合得分”为 $\text{[math]}$ ，若规定：
  $\text{[math]}$ “赞成”的票数 $\text{[math]}$ 分 $\text{[math]}$ “不赞成”的票数 $\text{[math]}$ 分；
  $\text{[math]}$ ．
  求该作品的“综合得分” $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
22. (2024八上·靖边期末) 甲、乙两名队员参加射击选拔赛，他们两人10次射击训练的成绩情况如下：
甲队员： $\text{[math]}$ ；
乙队员的成绩如下图：
根据以上信息，整理分析数据如下：
队员
平均数(环)
中位数(环)
众数(环)
方差(环²)
甲
7.9
$\text{[math]}$
$\text{[math]}$
4.09
乙
$\text{[math]}$
7
7
$\text{[math]}$
1. （1）表格中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）求出 $\text{[math]}$ 的值，并判断哪名队员的成绩更稳定？
3. （3）若从甲、乙两名队员中选派其中一名队员参赛，你认为应选哪名队员？请结合表中的四个统计量，作出简要分析．
答案解析收藏纠错 + 选题
23. (2023八上·深圳期末) 小彬在今年的篮球联赛中表现优异．下表是他在这场联赛中，分别与甲队和乙队各四场比赛中的技术统计．
场次
对阵甲队
对阵乙队
得分
篮板
失误
得分
篮板
失误
第一场
21
10
2
25
17
2
第二场
29
10
2
31
15
0
第三场
24
14
3
16
12
4
第四场
26
10
5
22
8
2
平均值
$\text{[math]}$
11
2
23.5
13
2
1. （1）小彬在对阵甲队时的平均每场得分 $\text{[math]}$ 的值是分；
2. （2）小彬在这8场比赛的篮板统计数据中，众数是，中位数是；
3. （3）如果规定“综合得分”为：平均每场得分 $\text{[math]}$ 平均每场篮板 $\text{[math]}$ 平均每场失损 $\text{[math]}$ ，且综合得分越高表现越好．利用这种方式，我可以计算得出小彬在对阵乙队时的“综合得分”是37.1分．请你比较小彬在对阵哪一个队时表现更好，并说明理由．
答案解析收藏纠错 + 选题
24. (2020八上·垦利期末) 在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m），绘制出如下的统计图①和图②，请根据相关信息，解答下列问题：

（Ⅰ）图1中a的值为 ▲ ；

（Ⅱ）求统计的这组初赛成绩数据的平均数、众数和中位数；

（Ⅲ）根据这组初赛成绩，由高到低确定9人进入复赛，请直接写出初赛成绩为1.65m的运动员能否进入复赛．

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

北师大版数学八年级上册《第六章数据的分析》单元提升测试卷

副标题：

*注意事项：

北师大版数学八年级上册《第六章数据的分析》单元提升测试卷

试题分析

总体分析

题量分析

难度分析

知识点分析

考生	笔试 $\text{[math]}$	面试 $\text{[math]}$
甲	$\text{[math]}$	$\text{[math]}$
乙	$\text{[math]}$	$\text{[math]}$
丙	$\text{[math]}$	$\text{[math]}$

领口大小 $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
销量 $\text{[math]}$ 件	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

学校	平均分	中位数	众数
$\text{[math]}$ 校	$\text{[math]}$	$\text{[math]}$	95
$\text{[math]}$ 校	93.5	95	$\text{[math]}$

专业评委	给分 $\text{[math]}$ 单位：分 $\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$

队员	平均数(环)	中位数(环)	众数(环)	方差(环²)
甲	7.9	$\text{[math]}$	$\text{[math]}$	4.09
乙	$\text{[math]}$	7	7	$\text{[math]}$

场次	对阵甲队			对阵乙队
场次	得分	篮板	失误	得分	篮板	失误
第一场	21	10	2	25	17	2
第二场	29	10	2	31	15	0
第三场	24	14	3	16	12	4
第四场	26	10	5	22	8	2
平均值	$\text{[math]}$	11	2	23.5	13	2

项目	完成作业	单元测试	期末考试
成绩	65	75

小学

初中

高中

北师大版数学八年级上册《第六章 数据的分析》单元提升测试卷

副标题：

*注意事项：

北师大版数学八年级上册《第六章 数据的分析》单元提升测试卷

试题分析

总体分析

题量分析

难度分析

知识点分析

北师大版数学八年级上册《第六章数据的分析》单元提升测试卷

北师大版数学八年级上册《第六章数据的分析》单元提升测试卷